LeetCode刷题日记精选例题(解析+代码+链接)
文章目录
- 一、用栈模拟队列
- 二、用队列模拟栈
- 三、有效的括号
-
- 解法一
- 解法二
- 四、删除字符串中所有相邻重复项
- 五、逆波兰表达式求值
- 六、滑动窗口最大值
- 七、前k个高频元素
一、用栈模拟队列
因为队列先进先出,而栈先进后出,所以我们用两个栈,一个输入栈,一个输出栈来模拟队列,当添加数据时,将其加在输入栈,当输出数据时,输出输出栈的数据即可
题目链接
Stack<Integer> inStack;
Stack<Integer> outStack;
public MyQueue() {
inStack = new Stack<>();
outStack = new Stack<>();
}
//进栈
public void push(int x) {
inStack.push(x);
}
//出栈
public int pop() {
if (outStack.empty()){
//如果输出栈为空,则将输入栈中的全部元素移到输出栈
while (!inStack.isEmpty()){
outStack.push(inStack.pop());
}
}
return outStack.pop();
}
//返回队列首部元素,不出栈
public int peek() {
if (outStack.empty()){
//如果输出栈为空,则将输入栈中的全部元素移到输出栈
while (!inStack.isEmpty()){
outStack.push(inStack.pop());
}
}
return outStack.peek();
}
//返回队列是否为空
public boolean empty() {
return inStack.empty()&&outStack.empty();
}
二、用队列模拟栈
Queue<Integer> queue1;
Queue<Integer> queue2;
public MyStack() {
queue1 = new LinkedList<>();
queue2 = new LinkedList<>();
}
public void push(int x) {
queue2.offer(x);
while (!queue1.isEmpty()){
queue2.offer(queue1.poll());
}
Queue temp = queue1;
queue1 = queue2;
queue2 = temp;
}
public int pop() {
return queue1.poll();
}
public int top() {
return queue1.peek();
}
public boolean empty() {
return queue1.isEmpty();
}
三、有效的括号
解法一
public static boolean isValid(String s) {
if (s.length()%2==1){
return false;
}
Map<Character,Character> map = new HashMap<>();
map.put(')','(');
map.put('}','{');
map.put(']','[');
char[] chars = s.toCharArray();
Stack stack = new Stack();
for (char aChar : chars) {
if (stack.size()>0&&map.containsKey(aChar)&&map.get(aChar).equals(stack.peek())){
stack.pop();
}else {
stack.push(aChar);
}
}
return stack.size()==0;
}
解法二
public static boolean isValid(String s) {
char[] chars = s.toCharArray();
Stack<Character> stack = new Stack();
for (char aChar : chars) {
if (aChar=='('){
stack.push(')');
}else if (aChar=='['){
stack.push(']');
}else if (aChar=='{'){
stack.push('}');
}else if (stack.isEmpty()||stack.peek()!=aChar){
return false;
}else {
stack.pop();
}
}
return stack.isEmpty();
}
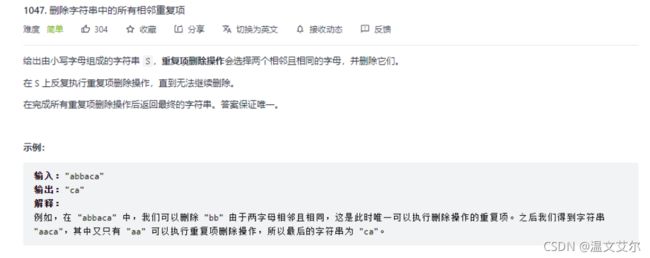
四、删除字符串中所有相邻重复项
思路解析:
和我们平时玩的消消乐的原理差不多,让元素入栈,判断将要入栈的元素与已经入栈的顶层元素是否相同即可
//ArrayDeque会比LinkedList在删除元素这一点外要快
public static String removeDuplicates2(String s) {
ArrayDeque<Character> stack =new ArrayDeque();
for (int i=s.length()-1;i>=0;i--){
if (!stack.isEmpty()&&stack.peek()==s.charAt(i)){
stack.pop();
}else {
stack.push(s.charAt(i));
}
}
StringBuilder sb = new StringBuilder();
while (!stack.isEmpty()){
sb.append(stack.pop());
}
return new String(sb);
}
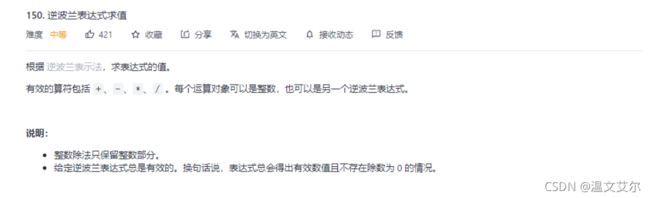
五、逆波兰表达式求值
这道题可以看我以前写的博文,对逆波兰表达式的介绍与代码实现
一文介绍逆波兰表达式及求值实现

题目链接
逆波兰表达式遵从的原则无非就是,数字入栈,有符号位则弹出栈顶的两个数字进行计算,再将结果入栈
public static int evalRPN(String[] tokens) {
Deque<Integer> stack = new LinkedList<>();
for (String token : tokens) {
char c = token.charAt(0);
if (!isOper(token)){
stack.addFirst(Integer.parseInt(token));
}else if (c=='+'){
stack.push(stack.pop()+stack.pop());
}else if (c=='-'){
stack.push(-(stack.pop()-stack.pop()));
} else if (c=='*'){
stack.push(stack.pop()*stack.pop());
}else{
int num1 = stack.pop();
int num2 = stack.pop();
stack.push( num2/num1);
}
}
return stack.pop();
}
//判断字符是否为符号
private static boolean isOper(String s){
return s.length() == 1 && s.charAt(0) <'0' || s.charAt(0) >'9';
}
六、滑动窗口最大值
此题我们需要解决滑动窗口的移动问题,以及如何选出每次移动的最大值,我们可以自定义一个队列,在添加元素时进行操作,使队列保持一种递减趋势,这样每次出队列的元素一定会是本轮中的最大值,每次移动使队首元素出队,下一个数组元素进入队尾
public class MQueue {
Deque<Integer> deque = new LinkedList();
//出队列
public void poll(int value){
if (!deque.isEmpty()&&value==deque.peek()){
deque.poll();
}
}
//进队列,保证队列递减
public void add(int value){
while (!deque.isEmpty()&&value>deque.getLast()){
deque.removeLast();
}
deque.add(value);
}
//展示队列首部元素
public int peek(){
return deque.peek();
}
}
class Solution{
public static int[] maxSlidingWindow(int[] nums, int k){
if (k>nums.length){
return null;
}
int[] arr = new int[nums.length-k+1];
MQueue mQueue = new MQueue();
int temp=0;
//加入初始元素
while (temp<k){
mQueue.add(nums[temp]);
temp++;
}
arr[0]=mQueue.peek();
for (int i=k;i<nums.length;i++){
//移除滑动窗口首部元素,判断其是否与数组元素一致,一致则删除,否则不做变化
mQueue.poll(nums[i-k]);
//添加新元素
mQueue.add(nums[i]);
//队列顶部元素一定为最大值
arr[i-k+1]=mQueue.peek();
}
return arr;
}
}
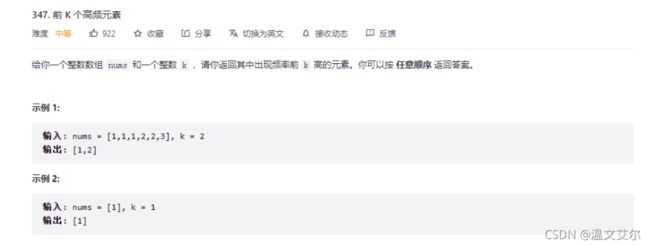
七、前k个高频元素
解题思路:
> 此题我们面临三个问题
> 1. 统计元素出现的频率
> 2. 对频率进行排序
> 3. 找出频率前k高的元素
对于问题1,我们使用map集合实现,问题二我们采用小顶堆,当堆内元素数量大于k时,每次将频率最小的元素弹出堆顶,然后将堆重元素放入数组进行返回
public static int[] topKFrequent(int[] nums, int k) {
if (nums.length==k){
return nums;
}
int[] arr = new int[k];
Map<Integer,Integer> map = new HashMap<>();
for (int num : nums) {
map.put(num,map.getOrDefault(num,0)+1);
}
PriorityQueue<Map.Entry<Integer,Integer>> queue = new PriorityQueue<>((v1,v2)->v1.getValue()-v2.getValue());
Set<Map.Entry<Integer, Integer>> entries = map.entrySet();
for (Map.Entry<Integer,Integer> entry:entries){
queue.offer(entry);
if (queue.size()>k){
queue.poll();
}
}
//将堆中元素的前k个元素放到数组中
for (int i=k-1;i>=0;i--){
arr[i]=queue.poll().getKey();
}
return arr;
}