每日一书丨知乎大V王赟Maigo出书了,14万关注、23万赞同
无论在学生时代还是职场生活,但凡遇到数学问题,总是让一部分人很挠头。有时候很羡慕那些数学好的学霸,他们总能轻轻松松搞定一切数学问题,更重要的是还能将复杂的问题用最简单的话讲解清楚。而王赟就是这样一位学霸。
(王赟老师知乎首页)
第一次认识王赟老师是在知乎上,当时看到他的问答,觉得清晰受用。后来发现他居然在图灵出书了,小编甚是激动呀!
翻了两天,终于把这本书都看完了。虽然里面部分题目的知识点已经忘得差不多了,但是有些题目看到王老师的解题思路,忍不住拍大腿:“居然还能这么解!”看书过程中还不停地点头,“原来是这样”“我咋就没想到”“不错不错这次会了”......就这样沉醉了两天,看到最后一页的时候竟然有点忧伤,因为后边没有了,也确实没看够。
就是这样一本小书,不那么厚,但是内容绝对会让你意犹未尽,并且不断发出“柳岸花明又一村”的感叹。如果你对数学有兴趣不妨来跟着作者的思路一起研究,保证你收获满满。
如此有意思的一本书,我们来近距离了解一下吧~
本书内容
第一章~第二章
这部分作者从两个简单的问题讲起,带你体会数学中“形”的直观与“数”的严谨。我国数学家华罗庚曾经说过:“数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休。”本书第一章研究一道关于碰撞的物理问题,它的巧妙解法体现了怎样通过“形”的方式使“数”的问题变简便。第二章介绍“超级任务”与 Ross-Littlewood 悖论,会涉及微积分中“一致收敛”的概念,仅通过形象思考不容易看清全貌,必须进行严谨的“数”的分析。
(我有一个罐子,一开始是空的。在 t = 1 秒时,我往罐里放 10 个球(编号 1∼10),再把 1 号球拿出来;在 t = 2 秒时,我把 11∼20 号球放到罐里,再把 2 号球拿出来;在 t = 3 秒时,我把 21∼30 号球放到罐里,再把3 号球拿出来;以此类推。问:到最后,罐子里有几个球?)
第三章~第六章
之后的几章,则通过深入分析几个看似简单的问题,带你领略数学中若干分支深处的风景。第三章研究在平面与球面上排列点阵(像向日葵花序那样)的问题,其探索过程主要涉及连分式的知识。第四章至第六章的几个问题都涉及概率与随机过程:第四章的“小黄鸭”问题,由二维平面与三维空间中的形象思考上升到高维空间中的严谨推理;第五章探讨“赌徒”的必胜策略,用到了随机过程中“鞅”的停时定理,以及谱分析法;第六章研究“洗牌”算法的一种错误实现中出现的神秘常数,会触及“ q-Pochhammer 符号”这种特殊函数。
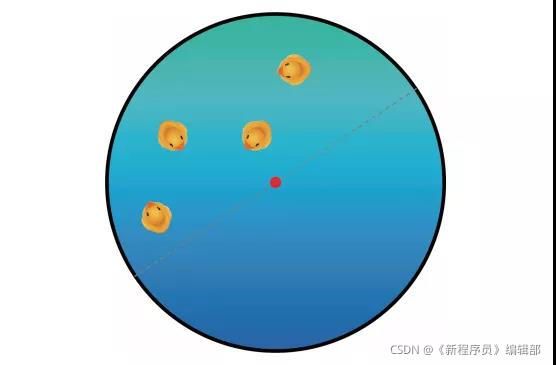
(有趣的小黄鸭问题:4 只小黄鸭分别随机地出现在一个圆形水池中的任意一点。它们位于同一个半圆内的概率是多少?)
数学与程序设计,是亲密如孪生姐妹的两个学科。在数学研究中遇到问题时,可以借助编程来获得灵感和验证结果;用数学方法研究出的结论,也能指导我们写出更短、更快、更好的程序。第三章至第六章的探索过程,都以计算机编程作为辅助手段,而第七章至第十一章,则以编程本身为研究对象。如果你正在学习算法与数据结构,这几章的内容会让你的头脑得到很好的锻炼。
第七章~第十一章
第七章至第九章,都取材于棋牌类游戏。第七章研究“ n 皇后”问题,第八章研究“24 点”算式,这两章的重点都在于枚举法的优化。第九章介绍 Sprague-Grundy 定理:它能够快速找出一种棋类游戏的必胜策略,但它的形式匪夷所思,这一章就介绍了提出该定理的思路。第十章介绍 Matlab 的数据可视化函数如何因为一个 bug 而效率异常低下,以及我想到的并不复杂的优化方案。第十一章则是对树这种数据结构进行一番操练,让你扎实掌握树形结构的序列化方法。
(“八皇后”是入门编程时的一道经典例题:在一个 8 × 8 的棋盘上放置 8 个皇后,要求任意 2 个皇后不能位于同一行、同一列,或同一条 45 度斜线上(图 7.1所示为此问题的一个解)。问:一共有多少种放法?)
本书有哪些特色
-
可以入选大厂面试题的题目。一个个看似简单的问题背后,都蕴含着并不简单的原理。
-
教你像科学家一样思考问题。通过全面严谨的思维训练,拓展你的思考深度。
-
让你轻松有趣地学好数学,书中示例生动,语言风趣,助你轻松理解高深的知识点。
- 全彩印刷,辅以大量精巧的图画。视觉体验更佳,核心内容一目了然。
这本书适合谁读
适合理工科的本科学生阅读。在阅读过程中,可以预习或者复习微积分、线性代数、概率论等多门数学知识,并体验用它们解决实际问题的乐趣。涉及编程的部分,使用的编程语言主要是Python和Matlab,这两种语言最能体现“简洁”的特点。如果你是对数学有自己研究的文科生,那这本书也适合你一一钻研。
本书讨论了一些源自日常生活的数学问题,用数学思维和计算机思维,讲解了巧妙的解题思路。一个个看似简单的问题,细究后却发现别有洞天。本书会带领读者一起来到数学研究的前沿阵地,享受思考的乐趣,感受数学的奥妙。读者在探究问题的过程中,可以学习和培养巧妙的数学思维和计算机思维,灵活应用知识,用四两拨千斤之巧力去解决生活、学习以及工程问题。 本书是一本标新立异又具有思想深度的思维训练书,适合理工科专业的本科生、研究生,以及对数学、计算机有兴趣的读者阅读。
作者是谁
王赟(Maigo):Facebook 语音组研究科学家。2006至2010年就读于清华大学电子工程系,并以第一的成绩进入美国卡内基梅隆大学(CMU);2010至2018年于卡内基梅隆大学计算机学院语言技术研究所攻读博士学位,主攻方向为语音识别、音频事件检测。曾于2004年、2005年参加全国信息学奥林匹克竞赛(NOI),并分别获得铜牌、银牌;此后曾辅导多名同学参加互联网公司的面试。于业余时间自学了日语、韩语、西班牙语、法语、越南语5门外语及中古汉语,并制作了安卓应用“汉字古今中外读音查询”。日常活跃于知乎,擅长回答数学、计算机、语言类问题,并在知乎专栏发表多篇优质文章,关注者超过14万。
目录一览
第一章 一道弹性碰撞的物理题,结果为什么会出现π? 1
1.1 碰撞的滑块 1
1.2 隐藏的椭圆 3
1.3 把椭圆“捏”成圆 5
第二章 超级任务与一致收敛 8
2.1 Ross-Littlewood悖论 8
2.2 逐点收敛与一致收敛 9
第三章 怎样在球面上“均匀”排列许多点? 13
3.1 神奇的斐波那契网格 13
3.2 从平面点阵入手 19
3.2.1 连分式与丢番图逼近 20
3.2.2 模式与模式图 22
3.2.3 连分式中的大项对模式的影响 30
3.2.4 斐波那契网格为什么混乱又密集? 32
3.2.5 总结 36
3.3 回到球面点阵 37
第四章 一道“小黄鸭”概率题及其有趣扩展 40
4.1 “小黄鸭”原题 40
4.2 高维情况初探 44
4.3 高维情况再探 48
4.4 高维情况的解决 54
4.5 编程验证 30
第五章 “赌徒”的征程 66
5.1 引子 66
5.2 递推法的困境 68
5.3 鞅的停时定理 75
5.4 会长大的笼子 80
5.5 靠谱的谱分析 83
5.6 尾声 88
第六章 一种错误的洗牌算法,以及乱排常数 90
6.1 乱排常数的起源 90
6.2 乱排常数的推导 95
6.3 乱排常数的简洁形式 101
6.4 乱排常数的几个推广 103
第七章 用位运算速解n皇后问题 108
7.1 解法一:步步回眸 109
7.2 解法二:雁过留痕 111
7.3 解法三:以一当百 113
7.4 解法四:弹无虚发 116
7.5 解法五:精益求精 119
7.6 总结 120
第八章 如何不重复地枚举24 点算式? 122
8.1 朴素的枚举法 122
8.1.1 算式的表示方式 123
8.1.2 朴素的枚举算法 125
8.1.3 算式重复的统计 126
8.1.4 算式重复的原因 127
8.2 避免由交换律、结合律、独立运算顺序不唯一造成的重复 129
8.2.1 避免由“交换律”造成的重复 129
8.2.2 避免由“结合律”造成的重复 130
8.2.3 避免由“独立运算顺序不唯一”造成的重复 133
8.2.4 小结 135
8.3 避免由去括号、反转减号造成的重复 136
8.3.1 避免由“去括号”造成的重复 137
8.3.2 避免由“反转减号”造成的重复 138
8.3.3 总结 143
第九章 Sprague-Grundy定理是怎么想出来的? 145
9.1 游戏介绍 145
9.2 策梅洛定理 148
9.3 游戏状态的组合 149
9.4 Sprague-Grundy数的提出 151
9.5 状态组合时Sprague-Grundy数的运算规则 154
9.5.1 规则的发现 154
9.5.2 规则的证明 156
9.6 Sprague-Grundy定理的完整表述 157
第十章 小算法题,大应用:如何“掰平”一个不单调的序列? 159
10.1 如何“掰平”一个不单调的序列? 159
10.1.1 Matlab的掰平算法 160
10.1.2 高效的掰平算法 162
10.2 “掰平”算法的应用:multi-dimensional scaling 163
10.3 附记 168
第十一章 二叉树怎样序列化才能重建? 169
11.1 几种常见的序列化方法 169
11.1.1 仅使用一种遍历的序列化方法 169
11.1.2 使用两种遍历的序列化方法 170
11.1.3 二叉搜索树(BST)的序列化方法 173
11.2 二叉树序列化能够重建的充分条件 175
11.3 “不含重复元素”的必要性探讨 176
参考文献 180
(声明:本文转载自“图灵教育”微信公众号。)