排序算法:冒泡,选择,插入,希尔以及堆排序
冒泡排序:时间复杂度O(N^2),空间复杂度O(1),稳定排序

这里的我们使用冒泡排序对数据升序排序,从后往前冒,每冒完一趟我们都会找到这一堆数据(待排序的数据)中最小的一个,并且该最小的数据就在待排序的数据中第一个位置上,此时我们修改有序的区间,再进行下一趟的冒泡排序,并且已经被排好的数据就不会二次被进行排序(二次排序是不必要的,这里就是借用一个有序区间避免了这种不必要)。
#include测试结果:

选择排序:时间复杂度O(N^2),空间复杂度O(1),不稳定排序

#include
#include"swap.h"
//选择排序,升序排序,(从前往后遍历)
void SelectSort(int arr[],int len)
{
if(len <= 1)
{
//不需要排序
return;
}
//[0,bound):有序区间
//[bound,len):待排序区间
int bound = 0;
for(;bound < len;bound++)
{
int cur = bound+1;
for(;cur < len;cur++)
{
if(arr[bound] > arr[cur])
{
//较大的数往后移
//每遍历完一趟,最小的数就排了在第一个位置
swap(&arr[bound],&arr[cur]);
}
}
}
return;
}
//测试代码与冒泡排序测试代码相同,只是调用函数不同,这里不再给出 测试结果:
插入排序:时间复杂度O(N^2),空间复杂度O(1),稳定排序
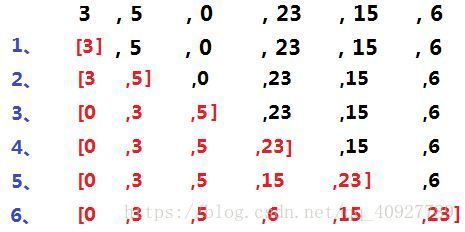
插入排序就是找到一个值,然后将这个值插入到有序区间中去,插入完成以后依旧有序,直到所有的数据插入完毕,排序就完成了。
#include 测试结果:
希尔排序:时间复杂度,取决于步长,此处对于希尔序列来说是O(N^2),空间复杂度O(1),不稳定排序
希尔排序是记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。
其中我们使用了希尔步长的概念,这里的作用就是将元素每隔希尔步长的距离的元素分为一组,这样就将一整组元素分为多个组,然后再将这多个组的每一个组采用直接插入排序的方法进行排序,然后在改变希尔步长值,继续分组排序,这样数据就越来越趋于有序状态,直到最后希尔步长为1,最后进行一次插入排序之后我们整体的希尔排序就算完成了。
#include
#include"sort.h"
//希尔排序
void ShellSort(int arr[],int len)
{
if(len <= 1)
{
//不需要排序
return;
}
int gap = len/2;
//第一重循环,用于生成步长序列
for(;gap > 0;gap /= 2)
{
//此处相当于插入排序中的bound= 1
int bound = gap;
//第二重循环进行插入排序
for(;bound < len;bound++)
{
//bound_value为待插入元素
int bound_value = arr[bound];
//第三重循环,线性表的查找和搬运
int cur = bound;
//cur-=gap就是在找到同组元素的上一个元素
for(;cur >= gap;cur -= gap)
{
if(arr[cur-gap] > bound_value)
{
//搬运
arr[cur] = arr[cur-gap];
}
else
{
//找到了合适的位置存放bound_value
break;
}
}//第三重循环结束
arr[cur] = bound_value;
}//第二重循环结束
}//第一重循环结束
return;
}
//测试代码与冒泡排序测试代码相同,只是调用函数不同,这里不再给出 测试结果:

堆排序:时间复杂度O(N*logN),空间复杂度O(1),不稳定排序
堆排序我们之前在学习堆的时候就实现过相关的代码,今天这里的代码实现思路哈当时的基本一样,知识其中的有些许操作稍有不同。
首先我们借助堆把数组中的元素创建为一个堆(升序建大堆,降序建小堆,我们这里的实现采用升序排序建大堆),然后我们将堆顶元素和堆中的最后一个元素交换,此时堆顶元素,即该组数据中最大的元素就到了最末尾,然后我们调整除了该最大元素剩下的数据为一个新的大堆,依稀重复上述交换,调整堆的两步步骤,最终直到我们将堆中所有的数据处理完,排序就完成了。
#include
#include<string.h>
#include"sort.h"
#include"swap.h"
//方法1:下沉式调整
void AdjustDown(int arr[],int len,int index)
{
int parent = index;
int child = 2*parent+1;
while(child < len)
{
//由于此处我们要升序排序需要建立大堆
if(child+1 < len && arr[child+1] > arr[child])
{
child = child+1;
}
//经历上面的判定以后,
//child就指向了左右子树中比较大的那个
if(arr[parent] < arr[child])
{
swap(&arr[parent],&arr[child]);
}
parent = child;
child = 2*parent+1;
}
return;
}
//方法2:上浮式调整
void AdjustUp(int arr[],int len,int index)
{
(void)len;
int child = index;
int parent = (child-1)/2;
while(child > 0)
{
if(arr[parent] < arr[child])
{
swap(&arr[parent],&arr[child]);
}
else
{
break;
}
child = parent;
parent = (child-1)/2;
}
return;
}
//创建堆
void HeapCreate(int arr[],int len)
{
if(len <= 1)
{
return;
}
int i = (len-1-1)/2;
for(;i > 0;i--)
{
AdjustDown(arr,len,i);
}
AdjustDown(arr,len,0);
}
//删除堆顶元素
void HeapPop(int arr[],int len)
{
if(len <= 1)
{
return;
}
swap(&arr[0],&arr[len-1]);
AdjustDown(arr,len-1,0);
}
//堆排序
void HeapSort(int arr[],int len)
{
if(len <= 1)
{
//不需要排序
return;
}
//基于数组建一个堆(升序:大堆,降序:小堆)
HeapCreate(arr,len);
int i = 0;
for(;i < len-1;i++)
{
//第二个参数表示数组中那一部分是堆
//例如:第一次删除之前[0,len)为堆
//第二次删除之前[0,len-1)为堆……
HeapPop(arr,len-i);
//注意这里的删除其实并不是真的就将堆顶的
//这一个元素删除掉,其实只是将较大的值(堆顶元素)
//移动到了后面,然后修改了数组中的元素属于堆的区间
}
return;
}
//测试代码与冒泡排序测试代码相同,只是调用函数不同,这里不再给出