powell法-鲍威尔法详解-附案例matlab代码

powell法（共轭方向法、方向加速法）

基本思想

若沿连接相邻两轮搜索末端的向量 S 方向搜索，收敛速度加快。

因为两条平行线 S1与同心椭圆族相切，两个切点的连线 S 直指中心。称 S1与 S2 为共轭方向。

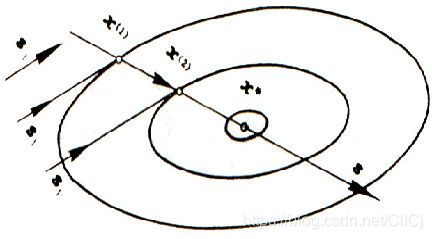
目的：以共轭方向打破振荡，加速收敛。

共轭方向的定义

共轭方向的性质

步骤

说明

1）若是正定二次函数，n 轮迭代后收敛于最优点 x* 。
2）若是非正定二次函数，则迭代次数增加。
3）若是 n 维问题，步骤相同。
搜索方向：第一轮迭代，沿初始方向组 Si(1) (i=1,2,…,n) 的 n 个方向和共轭方向 S(1)，搜索 n+1 次得极值点 xn+1(1) ；第二轮迭代，沿方向组 Si(2) ( i=1,2,…,n；i≠m ) 的 n-1 个方向和共轭方向 S(1)，构筑共轭方向 S(2) 搜索 n+1次得极值点 xn+1(2) 。其中，为保证搜索方向的线性无关，去除了 Sm(2) 方向 。
在第 k 轮迭代中，为避免产生线性相关或近似线性相关，需要去除前一轮中的某个方向 Sm(k)。

方法评价

1.计算步骤复杂;
2.是二次收敛方法，收敛快。对非正定函数，也很有效;
3.是比较稳定的方法。

算例

用Powell法求解：

初始点x0=[1,1],精度e=0.0001.

matlab求解

clear all
clc
 h0=0.1;
 x0=[1,1];
 e=[1,0;0,1];
 n=2;
for k=1:50  
    
    
    for i=1:n  
        x01=x0(1);x02=x0(2);d=e(i,:);  
        F0=ff(x0(1),x0(2));
        opt_step=goldsection(x01,x02,d,h0);
        x(i,:)=x0+opt_step*d; 
        F(i)=ff(x(i,1),x(i,2));
        D(i)=F(i)-F0;
    end
    for i=2:n  
        x01=x(i-1,1);x02=x(i-1,2);d=e(i,:);
        opt_step=goldsection(x01,x02,d,h0);
        x(i,:)=x(i-1,:)+opt_step*d; 
        F(i)=ff(x(i,1),x(i,2));
        D(i)=F(i-1)-F(i);
    end
 
    if abs(x(n,:)-x0)<1e-4%收敛条件
        break;
    end
    d=x(n,:)-x0;
    x(n+1,:)=2*x(n,:)-x0;
    [D_m,j]=max(D);
    F2=F(n);F3=ff(x(n+1,1),x(n+1,2));

    if F3=D_m/2*(0-F3)^2
        x01=x(n,1);x02=x(n,2);
        opt_step=goldsection(x01,x02,d,h0); 
        opt_step;
        x(n+1,:)=x(n,:)+opt_step*d;
        e(j,:)=[];
        e(n,:)=d;
        x0=x(n+1,:);
    else 
        if F2

目标函数：

function y=ff(x1,x2) 
y = 60-10*x1-4*x2+x1^2+x2^2-x1*x2;

区间搜索：

function [a,b]=search2(x01,x02,d,h0)  

a1=0; y1=ff(x01+d(1)*a1,x02+d(2)*a1);
h=h0;
a2=h; y2=ff(x01+d(1)*a2,x02+d(2)*a2);
if y2>y1  
    h=-h;
    a3=a1;y3=y1;
    a1=a2;y1=y2;
    a2=a3;y2=y3;
end
a3=a2+h;y3=ff(x01+d(1)*a3,x02+d(2)*a3);

while y30
    a=a1;b=a3;
else
    a=a3;b=a1;
end

所得结果

本优化问题的精确解为x0＝（8，6）

附注

黄金分割链接