八大排序算法(c语言)
八大排序算法
- 冒泡排序
-
- 冒泡排序思想
- 排序算法的实现
- 选择排序
-
- 选择排序思想
- 选择排序的实现
- 直接插入排序
-
- 直接插入排序思想
- 直接插入排序的实现
- 希尔排序
-
- 什么是希尔排序
- 为什么不直接使用插入排序
- 希尔排序代码实现
- 堆排序
-
- 首先一些基础概念
- 堆排序的思路
- 代码实现
- 快速排序
-
- 怎么做到快速排序
- 快速排序的代码实现
-
- 递归实现
- 非递归实现
- 归并排序
-
- 怎么做到归并排序
- 递归排序代码实现
- 基数排序
-
- 关于基数排序的思想
- 基数排序代码实现
冒泡排序
冒泡排序思想
将待排序数据序列的相邻两个数据(0,1 1,2 2,3 3,4 。。。 n-2, n-1)进行比较,然后将大的数据向后交换。一趟比较之后,就可以将最大的数据交换到最后。接下来,在对剩余的数据(除过最后一个数据)在进行冒泡排序。经过n-1次后,整个数据序列就有序了。

例:有这样一个无序数组。将下标0和1的两个数字比较,如果前面比后面大则将两个数字交换,随后继续比较下标1和2两个数字。

81 与 79 相比 81 大,则将 81 放在 下标2 ,79放在 下标1.

经过一次从0and1比较一直到8and9比较后

尽管现在数组依然无序,但是我们将数组中最大的元素99放在了下标9。
这样通过不断的0and1比较再到7and8比较又将第二大的元素放在了下标8。
0and1比较到6and7–5and6–4and5–3and4–2and3–1and2
这个时候除了下标0and1剩下都已经有序
继而在最后比较0and1总共比较 9次!

冒泡算法
时间复杂度: 等差数列 O(n^2)
空间复杂度: O(1)
稳定性: 稳定的
排序算法的实现
#include
在第一个for里,之所以 i
选择排序
选择排序思想
先遍历一遍待排序数据,从中标记出最大的数字(或者最小的数字)的位置,将标记出的数据与当前最后一个或者第一个数据进行交换。这一趟就是找到最大的或者最小的数字,并且将其放到一个合适的位置。
循环执行此过程,直到只剩下一个数字。

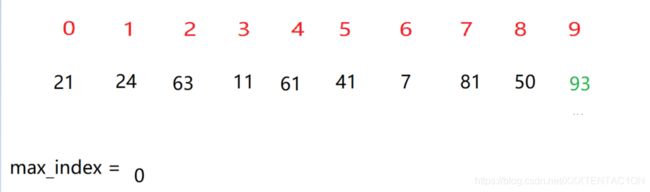
例 此数组遍历寻找数组中最大的元素



例如此时,下标4 的数字93>63,则max_index=4。然后继续向后比较

一直比较到最后一位时,93依旧是最大数,则将下标4(max_index)与下标9(数组最后一位下标)的数组交换,随后进行新一轮的比较。

选择排序的实现
选择排序
时间复杂度: 等差数列 O(n^2)
空间复杂度: O(1)
稳定性: 不稳定
void SelecySort(int* arr, int len)
{
for (int i = 0; i < len - 1, i++)
{
int max_index = 0;
for (int j = 0; j < len - i; j++)
{
if (arr[j] > arr[max_index]) max_index = j;
}
Swap(&arr[max_index], &arr[len - i - 1]);
}
}
完整代码
#include直接插入排序
直接插入排序思想
将待排序序列看成两部分,左部分为已经有序的,右部分为无序的(第一次左部分只有一个数据)。循环从右部分拿一个数据插入到左部分中(从左部分的最后一个数据开始比较,如果比拿的数据大,则将其向后挪动一个位置,直到找到比他小的,或者左部分遍历完),并且使得插入后的结果依旧有序。直到有部分没有数据为止!
即将数组分为左右两部分,一开始左部分只有一个元素,左右部分想接触的两个数进行比较,若左边小于右边则不进行操作,若右边小于左边则,两元素交换并且继续向前比较,直到找到比该元素小的数字或者该元素已经是左部分最左边的元素。
直接插入排序
时间复杂度: 等差数列 O(n^2)
数据序列已经有序,则能达到最好时间复杂度: O(n)
数据趋于有序(部分有序): 时间复杂度就可以趋于 O(n),–》 数据越有序,时间复杂度越低。
空间复杂度: O(1)
稳定性: 稳定的
直接插入排序的实现
void InsertSort(int* arr, int len)
{
for (int i = 1; i < len ; i++)
{
int tmp = arr[i];
int j = i - 1;
while (arr[j] > tmp && j >= 0)
{
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = tmp;
}
}
完整代码
#include希尔排序
什么是希尔排序
希尔排序也叫做:缩小增量排序。 分组(分组的组数需要循环递减,直到减为1)排序。
先将待排序序列分成若干组,然后使用直接插入排序在组内排序。循环着将分组数减小,执行以上过程。直到分组减为1. 所有的分组数都互质。
分组可为任意数字,且每次分组数都比上一次分组要小,直至分组数为1。

为什么不直接使用插入排序
相比较插入排序,希尔排序输入直接插入排序的一种,但是在两种算法的比较上
希尔排序: 就是直接插入排序的优化, 数据越有序,排序越快
时间复杂度: 时间复杂度是与增量序列相关的函数 O(n^1.3~1.5)
空间复杂度: O(1)
稳定性: 不稳定
直接插入排序
时间复杂度: 等差数列 O(n^2)
数据序列已经有序,则能达到最好时间复杂度: O(n)
数据趋于有序(部分有序): 时间复杂度就可以趋于 O(n),–> 数据越有序,时间复杂度越低。
空间复杂度: O(1)
稳定性: 稳定的

对于一个长度为10000的需要排序的数组,希尔排序只需要更少的比较次数与交换次数。
希尔排序代码实现
void Shell(int *arr, int len, int width)
{
for(int i = width; i < len; ++i)
{
int tmp = arr[i];
int j = i - width;
for(; j >= 0 && arr[j] > tmp; j -= width)
{
arr[j+width] = arr[j];
}
arr[j+width] = tmp;
}
}
void ShellSort(int *arr, int len)
{
int group[] = {
5, 3, 1};
for(int i = 0; i < sizeof(group)/sizeof(group[0]); ++i)
{
Shell(arr, len, group[i]);
}
}
很显然,希尔排序不过对直接插入排序前进行了一次分组。分组使得希尔排序对于大量的数据处理更有优势,但是也增加了不稳定性。
堆排序
首先一些基础概念
二叉树: 每个结点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。二叉树常被用于实现[二叉查找树]和二叉堆。
满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是(2^k) -1 ,则它就是满二叉树
完全二叉树: 一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树。
堆: 堆通常是一个可以被看做一棵完全二叉树的数组对象。堆总是满足下列性质:
- 堆中某个结点的值总是不大于或不小于其父结点的值;
- 大根堆: 每个子树的父节点都大于等于其左、右孩子 --》 根是最大的
- 小根堆:每个子树的父节点都小于等于其左、右孩子 --》 根是最小的
- 堆总是一棵完全二叉树
完全二叉树的数组存储的性质
1、如果一个节点的下标为i, 则其左孩子的下标为:2*i+1, 右孩子: 2*i+2
2、如果一个孩子的下标为i, 则其父节点的下标为: (i - 1) / 2
堆排序的思路
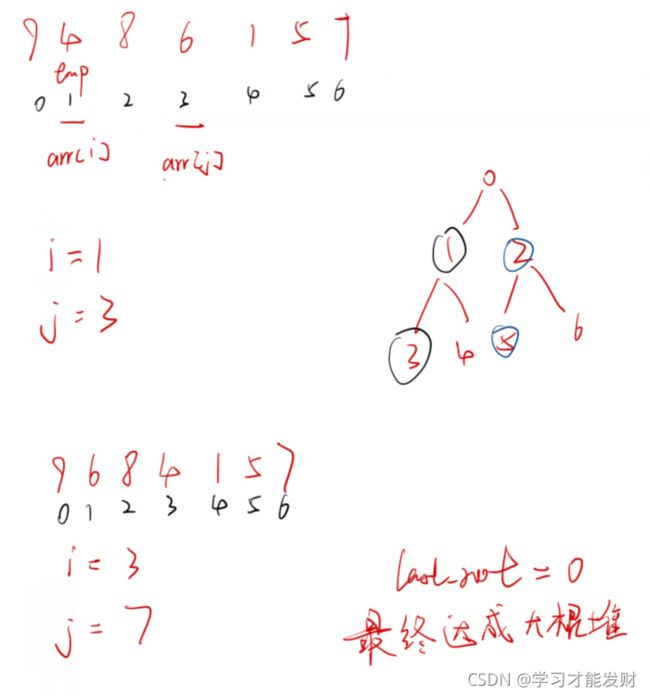
1.首先将待排序的数组构造成一个大根堆,此时,整个数组的最大值就是堆结构的顶端
2.将顶端的数与末尾的数交换,此时,末尾的数为最大值,剩余待排序数组个数为n-1
3.将剩余的n-1个数再构造成大根堆,再将顶端数与n-1位置的数交换,如此反复执行,便能得到有序
堆排序
时间复杂度: O(nlogn)
空间复杂度: O(1)
稳定性: 不稳定
O(logn)
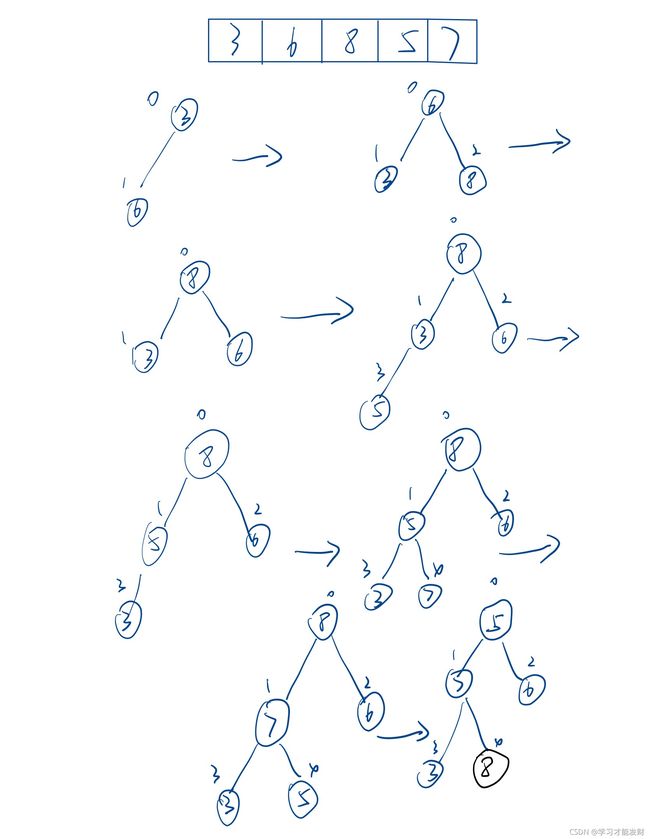
首先构造大根堆,即比较左右孩子是否大于父节点,如果大于则交换,最终得到根节点就是最大数。随后将根节点与最后的节点进行交换,重复多次便有序。

代码实现
void OneAdjust(int *arr, int len, int root)
{
int tmp = arr[root];//父节点
int i = root;
int j = 2 * i + 1;//最后一个树杈的左孩子
while(j < len)
{
if(j + 1 < len && arr[j] < arr[j+1]) j++; // j 就是大孩子的下标
if(arr[j] < tmp) break;
arr[i] = arr[j];
i = j;
j = 2 * i + 1;
}
arr[i] = tmp;
}
// O(nlogn)
void CreateHeap(int *arr, int len)
{
int last_root = (len - 2) / 2;//最后一个节点的父节点
for(int i = last_root; i >= 0; --i)//循环结束后 达成大根堆
{
OneAdjust(arr, len, i);
}
}
//O(nlogn)
void HeapSort(int *arr, int len)
{
CreateHeap(arr, len);
// O(nlogn)
for(int i = 0; i < len - 1; ++i)
{
Swap(&arr[0], &arr[len-1-i]);//将大根堆根节点和最后一个节点交换
//然后忽略最后一个节点重复前面的过程
OneAdjust(arr, len-1-i, 0);
}
}
快速排序
怎么做到快速排序
-
在数组中选一个基准数(通常为数组第一个);
-
将数组中小于基准数的数据移到基准数左边,大于基准数的移到右边;
-
对于基准数左、右两边的数组,不断重复以上两个过程,直到每个子集只有一个元素,即为全部有序。
left和right分别为待排序序列的区间左右下标,先选取一个数据作为基准,right从后向前找比基准小的数据,找到后存储到left位置(而不是交换当前left和right位置的数据),然后left从前向后找比基准大的数据,找到后存储到right位置。直到left和right相遇,将基准数据存储到left位置。
由以上过程就可以根据基准数据将整个序列分成左右两部分。然后分别对左部分和右部分执行以上过程。直到左右部分没有数据或者只剩一个数据。

如果left下标或者right下标,在与基准比较后,没有移动,则直接移动left或right继续比较,而不是切换另一边进行比较。

快速排序
时间复杂度: O(nlogn)
空间复杂度: O(logn)
稳定性 : 不稳定
快速排序的代码实现
递归实现
int OneQuick(int *arr, int left, int right)
{
int i = left;
int j = right;
int tmp = arr[i];//Pivot 基准定义为 left 最左边数字
while(i < j)
{
while(i < j && arr[j] >= tmp) j--;//先对right比较
//大于基准则j--继续比较
arr[i] = arr[j];//否则将 right 存贮在 left 的位置
//而不是交换当前left和right位置的数据
while(i < j && arr[i] <= tmp) i++;//与上面同理
arr[j] = arr[i];
}
//i == j
arr[i] = tmp;//将 Pivot 的值存在left 与 right 下标交汇的地方
//这时候 该下标位置固定即排序完成
return i;
}
void Quick(int *arr, int left, int right)
{
int mod = OneQuick(arr, left, right);
if(mod - left > 1)//mod > 0
{
Quick(arr, left, mod - 1);//递归,新的组[left(0),mod-1]
}
if(right - mod > 1)//mod < len-1
{
Quick(arr, mod + 1, right);//递归,[mod+1,right(len-1)]
}
}
void QuickSort(int *arr, int len)
{
Quick(arr, 0, len-1);
}
非递归实现
栈实现
通过入栈出栈方式,将需要排序的组Pop出栈,同时排序完成会生成两个新的组,并将两个新的组入栈,同时在再一次出栈排序又会形成两个新的组,继而通过栈的方式实现了类似递归的方式。
/快排的非递归实现//
//栈实现
//通过入栈出栈方式,将需要排序的组Pop出栈,同时排序完成会生成两个新的组
//并将两个新的组入栈,同时在再一次出栈排序又会形成两个新的组
//继而通过栈的方式实现了类似递归的方式
typedef struct
{
int left;
int right;
}PairData;
typedef struct
{
PairData *data;
int top;
int size;
}Stack;
void InitStack(Stack *st, int init_size)
{
if(st == NULL) exit(0);
init_size = init_size > 0 ? init_size : 10;
st->data = (PairData*)malloc(sizeof(PairData) * init_size);
if(st->data == NULL) exit(0);
st->top = 0;
st->size = init_size;
}
int Empty(Stack *st)
{
if(st == NULL) exit(0);
return st->top == 0;
}
PairData Pop(Stack *st)
{
if(st == NULL) exit(0);
if(Empty(st)) exit(0);
st->top--;
return st->data[st->top];
}
void Push(Stack *st, PairData value)
{
if(st == NULL) exit(0);
if(st->top == st->size) exit(0);
st->data[st->top++] = value;
}
void Destroy(Stack *st)
{
if(st == NULL) exit(0);
free(st->data);
st->data = NULL;
st->top = st->size = 0;
}
void Quick2(int *arr, int left, int right)
{
Stack st;
int stack_size = 2 * ((int)(log10(right-left+1) / log10(2)) + 1);
//计算 栈的大小
InitStack(&st, stack_size);
PairData value = {
left, right};
Push(&st, value);
while(!Empty(&st))
{
value = Pop(&st);
int mod = OneQuick(arr, value.left, value.right);//一次排序
if(mod - value.left > 1)//一次排序后 left 组
{
PairData left_pair = {
value.left, mod-1};
//left == left 还是原来的left right == mod-1
Push(&st, left_pair);//入栈 等待Pop 进行排序处理
}
if(value.right - mod > 1)//与上面同理
{
PairData right_pair = {
mod+1, value.right};
Push(&st, right_pair);
}
}
Destroy(&st);
}
归并排序
怎么做到归并排序
将数据划分成不同的区间段(每个区间段已经有序),初始时,每个区间段只有一个数据。
将相邻两个区间段合并到一块。重复这个过程,直到只剩下一个区间段。

最终所有元素都在同一组,且保持有序
归并排序
时间复杂度: O(nlogn)
空间复杂度: O(n)
稳定性: 稳定的
递归排序代码实现
void Meger(int *arr, int len, int width, int *brr) // width每个段的数据量个数
{
int low1 = 0;
int high1 = low1 + width - 1;//一组几个元素
int low2 = high1 + 1;
int high2 = low2 + width - 1 < len - 1 ? low2 + width - 1 : len - 1;
int index = 0;
// 有两个归并段
while(low2 < len) //可以两个段组成一个段
{
// 两个段都有数据时
while(low1 <= high1 && low2 <= high2)
{
//比较大小,小的数字放入brr,且后移并继续比较
if(arr[low1] < arr[low2]) brr[index++] = arr[low1++];
else brr[index++] = arr[low2++];
}
// 只剩下一个段有数据,将有数据的段直接加入brr中
while(low1 <= high1) brr[index++] = arr[low1++];
while(low2 <= high2) brr[index++] = arr[low2++];
//这时候第一个段与第二个段合并排序完成
//需要继续进行第三个段与第四个段的合并排序
low1 = high2 + 1;
high1 = low1 + width - 1;
low2 = high1 + 1;
high2 = low2 + width - 1 < len - 1 ? low2 + width - 1 : len - 1;
}
// 只有一个段的情况
while(low1 < len) brr[index++] = arr[low1++];
//最后将brr赋值给arr,这时候arr就是完成整个合并段排序过程
for(int i = 0; i < len; ++i)
{
arr[i] = brr[i];
}
}
void MegerSort(int *arr, int len)
{
int *brr = (int*)malloc(sizeof(int) * len);
if(brr == NULL) exit(0);
for(int i = 1; i < len; i *= 2)//两段合并,直至只有一个段
{
Meger(arr, len, i, brr);
}
free(brr);//最终free掉brr的空间
}
基数排序
关于基数排序的思想
基数排序是针对有多个关键字(每个关键字的权重不同)的排序算法: 炸金花(花色,数字)。
![]()
基数排序时桶排序的一种推广,它所考虑的待排记录包含不止一个关键字。例如对一副牌进行整理,可将每张牌看做一个记录,包含两个关键字:花色、面值。一副理顺的牌是按如下顺序进行排放的:
![]()
针对于一组整形数据: 按照权重划分(个位,十位,百位,千位 … )。
按照从小权重到大权重进行处理。对于一个数据,拿到这一位的值,将原始数据存储到相应的队列中。一个有关键字取值范围的队列(0,1,2,3,4,5,6,7,8,9)。整个数据序列全部放入到队列后,按照队列顺序将其中的数据全部Pop出来,在放回到数组中。
基数排序数据之间不需要比较。
![]()
基数排序
空间复杂度: O(dn) d是关键字的取值范围
时间复杂度: O(wn) w是关键字的个数
稳定性: 稳定
基数排序代码实现
typedef struct
{
int *data;
int rear;
int head;
int size;
}Queue;
void InitQueue(Queue *que, int init_size)
{
if(que == NULL) exit(0);
init_size = init_size > 0 ? init_size:10;
que->data = (int*)malloc(sizeof(int) * init_size);
if(que->data == NULL) exit(0);
que->head = que->rear = 0;
que->size = init_size;
}
void ClearQueue(Queue *que)
{
if(que == NULL) exit(0);
que->head = que->rear = 0;
}
void PushQue(Queue *que, int value)
{
if(que == NULL) exit(0);
if(que->rear == que->size) return;
que->data[que->rear++] = value;
}
int EmptyQue(Queue *que)
{
if(que == NULL) exit(0);
if(que->head == que->rear) return 1;
return 0;
}
int PopQue(Queue *que)
{
if(que == NULL) exit(0);
if(EmptyQue(que)) return -1;
int reval = que->data[que->head];
que->head++;
return reval;
}
void DestroyQue(Queue *que)
{
if(que == NULL) exit(0);
free(que->data);
que->data = NULL;
que->head = que->rear = 0;
}
// 获取最大数的位数
int GetMaxWidth(int *arr, int len)
{
int max_value = 0;
for(int i = 0; i < len; ++i)
{
if(arr[i] > max_value)
{
max_value = arr[i];
}
}
int width = 0;
while(max_value) // 1234 1234 % 10
{
width++;
max_value /= 10;
}
return width;
}
//根据位数获取相应位上的值
int GetWidthValue(int value, int width)
{
while(width)
{
if(value == 0) return 0;
width--;
value /= 10;
}
return value % 10;
}
/*
空间复杂度: O(d*n) d是关键字的取值范围
时间复杂度: O(w*n) w是关键字的个数
稳定性: 稳定
*/
void RadixSort(int *arr, int len)
{
Queue que[10];
//十个数字,按每个数字分配一个大小为len的队列,有对应数字便入队
for(int i = 0; i < 10; ++i)
{
InitQueue(&que[i], len);
}
int max_width = GetMaxWidth(arr, len);//获取最大数的位数
for(int i = 0; i < max_width; ++i) // i==0 个位 i==1 十位
{
for(int j = 0; j < len; ++j) // 遍历整个待排序序列,按照i给定的位数将数据放到对应的队列中
{
int value = GetWidthValue(arr[j], i);//获取位数上相应的数值
PushQue(&que[value], arr[j]);
//在这里 将位数得到的数 放入到相应下标的队列中,并按队列顺序出队
//随后便得到按位排列好顺序的一组数据
}
int index = 0;
for(int k = 0; k < 10; ++k) // 遍历所有的队列,按照顺序将队列中的数据全部输出
{
while(!EmptyQue(&que[k]))
{
arr[index++] = PopQue(&que[k]);
}
ClearQueue(&que[k]);
}
}
for(int i = 0; i < 10; ++i)
{
DestroyQue(&que[i]);
}
}