扑克牌猜数字游戏规则_模式预测型吉尔布雷斯扑克牌魔术

作者简介： 杨秉翰(Douglas B.-H. Yang)，现就读于美国菲利普斯安多福学院(Phillips Academy Andover)。出生长大于香港，父母来自台湾。从小热爱数学以及魔术，受  Magical Mathematics 一书启发，利用自动机理论发明了模式预测型吉尔布雷斯扑克牌魔术，并撰以下报告。此报告曾获得 2018 年丘成桐中学科学奖(数学)北美区银奖，作者去年应邀参加芝加哥科学魔术会议。

本文英文题目为 Pattern Predictive Gilbreath Card Trick，中文版经作者授权刊登于《数理人文》杂志(订阅号：math_hmat)，未经许可，不得转载。

1. 绪论

台上魔术师拿出两副牌背颜色不同的扑克牌，正面朝下摆在桌上。两副牌各自切成两半，然后两副牌各自拿起半副，由魔术师本人或是交给观众成员，用交错式洗牌法(riffle shuffle, 又称梅花间竹式洗牌法)洗牌，让原本的两副牌混在一起，成为两副洗过的新牌。魔术师拿起第一副牌，两张牌为一组，将扑克牌亮给观众看，但亮牌前先请观众猜猜看，接下来亮出的一组牌是什么颜色组合(黑红、黑黑，还是红红)观众或许可以猜对几个组合，但一定会有猜错的时候，因为 26 个组合全部猜对的机率是 (1/3)²⁶；然而，魔术师却能成功预测每一组两张牌的颜色组合。接着，魔术师拿起第二副牌，提高预测的难度，还要预测每一组牌的花色强弱组合(方块与梅花弱、红心与黑桃强)。提高难度后，魔术师还是每一组牌都能正确预测。

这样的「模式预测型吉尔布雷斯扑克牌魔术」(Pattern Predictive Gilbreath Card Trick)，是知名的吉尔布雷斯扑克牌魔术(Gilbreath card trick)的变化版，加入互动元素。表演吉尔布雷斯扑克牌魔术时，一副牌洗过之后，两张牌为一组，每一组都刚好有一张红色牌、一张黑色牌。本文将介绍本魔术的原理，并探究其中蕴含的数学。进入正题前，本文会先回顾吉尔布雷斯原本的魔术以及德布因发明的变化版，再介绍本文提出的模式预测变化版以及背后的数学。

---

2. 吉尔布雷斯扑克牌魔术与德布因变体

加拿大魔术师诺曼‧吉尔布雷斯(Norman Gilbreath)在 50 年前运用数学原理，发明一种高强的扑克牌魔术。魔术师先准备一副牌扑克牌，整副牌颜色一红一黑交错出现(当然，观众不会知道这样的事前准备工作)，然后切成张数一样的两叠牌(或是任意从一副牌背朝上的一副扑克牌发出几张牌)，两叠牌交错洗牌之后，整副牌两张为一组，每组牌都是一张红、一张黑 [1]。同样的原则，也可以用在扑克牌花色与数字：1985 年，尼可拉斯‧戈维特‧德布因(Nicolaas Govert de Bruijn)发明这种魔术的变化版，让两叠牌不只红黑交错，花色强弱也交错出现。一副牌切成两叠后，一叠是方块(弱)与黑桃(强)交错，另一叠是梅花(弱)与红心(强)交错，两叠交错洗牌(这样的事前准备，同样不会让观众知道)。同样的道理，洗完牌之后每组两张牌一定会是一红一黑、一强一弱，或两者都是。德布因利用一个巧妙的数学自动机，证明他的魔术原理。这个自动机模型，反映整个交错洗牌过程各阶段的状态 [2]。基本上，自动机任两次转换，从一个状态转换到另一个状态，都可以证明是一红一黑、一强一弱，或是两者都是。不管是原本的吉尔布雷斯魔术，或是德布因发明的变化版，都让魔术师可以证明，普遍认为是最公平的交错式洗牌法，其实并不会改变每组两张牌的牌面性质，因此可以变出惊人的魔术。

事实上一副扑克牌经过交错式洗牌后，许多性质并不会改变。每次交错洗牌后，扑克牌的排列顺序，都称作吉尔布雷斯排列(Gilbreath permutation)。例如，在前述的两种吉尔布雷斯扑克牌魔术中，假设我们手上拿着两副红黑交错的扑克牌，利用交错式洗牌，洗完牌后，若将整副牌按顺序两两分为一组，会发现每一组牌都是一红一黑。

在继续讨论之前，我们先向较不熟悉的读者介绍一下交错式洗牌的方法。首先将一副牌切成两叠，分别用左右手拿起，两叠牌横放，用双手从上方握住，拇指扣紧。两叠牌一角重叠，用拇指控制，将两叠牌交错放下。每张牌放下时，我们就说这张牌「落下」。每一张牌落下时，就不再是手中那叠牌的底牌，而是下一张牌变成底牌。整个洗牌过程，到手中所有牌全部落下才算完成。这里必须强调，在表演魔术时，牌落下的顺序，是魔术师预测顺序的相反。换句话说，洗牌时首先落下的牌，在表演时是到最后才会让魔术师预测、亮给观众。

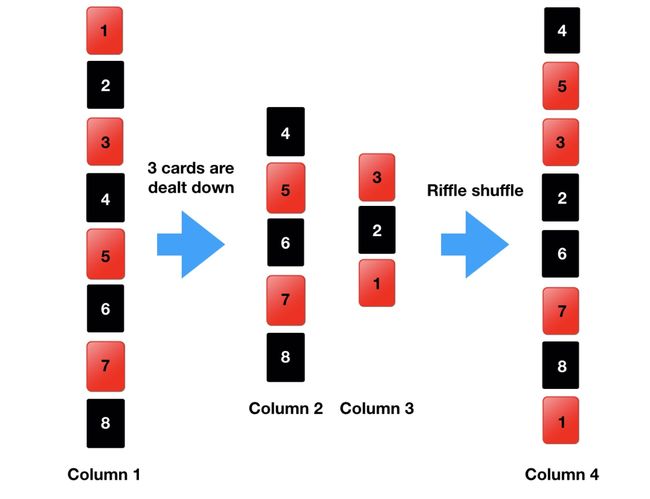
如果想了解交错式洗牌对整副牌的影响，可以想像有一副红黑交错排列的牌，第一张是红色、最后一张是黑色(图中第 1 列，请看 column 1)，假设发出三张牌，每一张发出的牌都叠在前一张牌的上方，如此面前就会有两叠牌，第一叠是剩下未发的牌(底牌为黑色，图中第 2 列，请看 column 2)，第二叠是发出的牌(底牌为红色，图中第 3 列，请看 column 3)，由于发牌的方式，这三张牌的顺序是发牌前的相反。若将这两叠牌洗牌，假设第一张放掉的牌是第二叠底部的红色牌(图中第 3 列 1 号牌)，第二张牌可能来自第一叠，也可能来自第二叠，但不论如何必定是黑色牌。假设下一张放掉的牌是第一叠的黑色牌(图中第 2 列 8 号牌)，那么再下一张可能是第一叠的红色牌(图中第 2 列 7 号牌)也有可能是第二叠的黑色牌(图中第 3 列 2 号牌)。假设下一张是第一叠的红色牌(图中第 2 列 7 号牌)，那么同理可知，下一张牌一定是黑色牌，因为洗牌者手中两叠的底牌都是黑色(图中第 4 列)。继续推论下去即可知，虽然洗完的牌不一定是完全红黑交错出现，但是如果依序两两一组抽牌，每一组牌一定都是一红一黑。这个现象称为吉尔布雷斯原则(Gilbreath principle)。

吉尔布雷斯发表这项戏法的原理后不久，德布因发明了变化版，加入花色元素。吉尔布雷斯的戏法，用的是两叠红黑交错的扑克牌，花色并无限制。德布因将这项戏法略加修改，两叠牌中有一叠是方块与黑桃交错，另一叠则是红心与梅花交错。方块与梅花是弱花色，黑桃与红心则是强花色，因此两叠牌不止是颜色交错，花色强弱也是交错出现。两叠牌透过洗牌合而为一后，牌的顺序看似随机，但其实若以两张为一组，每一组牌必定花色一强一弱，或是颜色一红一黑，也有可能两者都是。

为了用数学方式理解这个现象，德布因发明了以下确定有限状态自动机，反映两叠牌(一叠方块与黑桃、另一叠红心与梅花)洗牌的过程。

交错式洗牌自动机

本自动机有四种状态，每种状态都对应着交错洗牌时，两叠牌分别的两底牌的一个花色组合，弧线与箭头则代表洗牌过程：(1) 状态 p，两张底牌分别是红心与黑桃。(2) 状态 q，两张底牌是方块与红心。(3) 状态 r，两张底牌是梅花与黑桃。(4) 状态 s，两张底牌是方块与梅花。每一条路径旁都有标出字母与符号，代表洗牌时落下的牌的花色。H 代表红(Hearts)，D 代表方块(Diamonds)，C 代表梅花(Clubs)，S 代表黑桃(Spades)。

这个自动机的转移函数，套用在德布因的扑克牌魔术，指的就是在洗牌时一张底牌落下的动作。每当有一张底牌落下，手中两叠牌的底牌花色组合就会改变，也代表自动机从一个状态转换为另一个状态。假设目前的洗牌状态是状态 s，两张底牌分别是方块与梅花，那么假设放掉方块那张牌，就会沿着 D 弧线转换为状态 r，新的底牌组合是黑桃与梅花。洗牌结束后，魔术师是两张为一组预测扑克牌的组合。由于魔术师是每两张牌做一个牌面颜色或花色组合预测，每一组牌(也就是两张牌)都可以用一个双周期代表，也就是等于是走了自动机中的两条路径。换句话说，在表演魔术时，洗牌过程中每放掉两张牌，自动机状态就会沿着对应的弧线，转换两次。

本文第一节中描述的模式预测型吉尔布雷斯魔术，是将德布因发明的变化版，再进一步变化。读者应该记得，德布因的变化版中，每一组牌都是花色一强一弱、颜色一红一黑，或是两者都是，但这些组合的出现似乎是随机的。模式预测型吉尔布雷斯魔术，以德布因的发明为基础进一步发展，利用两副牌背颜色不同的扑克牌，分析这些组合出现的模式，再运用这些模式来进行预测，这样的预测正是本魔术的核心。

---

3. 模式预测吉尔布雷斯扑克牌魔术的秘密

我们的模式预测型吉尔布雷斯扑克牌魔术，是怎么样表演的呢？

表演开始前，魔术师必须先准备两副牌背颜色不同的扑克牌。魔术师先将两副牌各自用花色分类，然后将两副牌的方块与黑桃牌交错排成一叠、红心与梅花牌交错排成一叠，如此一来两副牌各自分成两叠，然后将两叠合併，又成为两副完整的扑克牌。这两副牌各自由两叠花色交错的牌构成。接着魔术师将两副牌收回盒子中，并且特别注意，其中一叠(记得一副牌由两叠牌组成)牌的底牌颜色必须与其他叠不同。表演开始时，魔术师拿出排列看似随机的两副牌，然后找出两副牌中方块与黑桃牌跟梅花与红心牌的交界，以此交界将两副牌各切成两叠。魔术师将每叠的底牌记在心中，然后一手拿起其中一叠牌，另一手内拿起另一副牌花色相反的一叠牌，两叠交错洗牌。(例如，一手拿起红色牌背的红心与梅花牌，另一手就是拿起蓝色牌背的方块与梅花牌，两叠交错洗牌。)剩下的两叠牌，可以交给一名观众洗牌。

本文将证明，经过这样的前置作业，洗过的牌将会有以下现象：任意连续两张牌，若牌背颜色不同，则正面颜色必然相同(两张红色或两张黑色)。两张牌若牌背颜色相同，正面必然是一红一黑。魔术师亮出前几组牌时，先要求观众猜猜两张牌的颜色会是相同还是不同，然后就可以利用以上资讯，将第一副牌两两发在桌上亮出，同时成功预测每一组牌颜色的异同，接着，魔术师拿起第二副牌，请观众猜测每组两张牌花色的强弱组合(黑桃与红心是强花色，方块与梅花是弱花色)。这个阶段的表演仍然是同样的规则：牌背相同的两张牌，花色必定是一强一弱；牌背相异的两张牌，花色强弱必定相同。

---

4. 魔术背后的数学

交错式洗牌中重组过程的特性，让我们(与魔术师)只要看到牌背的颜色，就可以判断每组两张牌的性质。这个推论过程，我们可以将德布因的自动机方法推广来表示。

解释本魔术的原理时，我们会着重在每一组两张牌牌背的异同，与该组牌的牌面特性之间的关系。这里定义的「牌面」是扑克牌显示数字与花色的一面，「牌背」则是相反的一面。由此我们可以定义「同背组合」是两张牌背相同颜色的牌，「异背组合」则是两张牌背颜色相异的牌。

---

5. 牌背颜色自动机

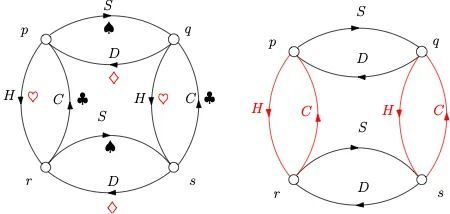
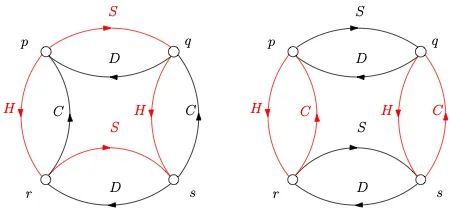
本模式用上两副牌，其中一副牌背是黑色，另一副牌背则是红色。图 (d) 中，我们根据牌背的颜色，将自动机的弧线上色，即成牌背颜色自动机。代表红心与梅花序列的弧线上红色，方块与黑桃序列的弧线则保持黑色。我们的牌背颜色自动机与德布因发明的自动机(图 (a))结构是一样的，图 (a) 的自动机接下来我们也会用上。

a. 交错式洗牌自动机(左)；d. 牌背颜色自动机(右)

想像魔术师手中有两叠牌，各自有两个花色交错排列，准备要洗牌。本例中，两张底牌是黑桃与梅花，如此一来本次洗牌的初始状态就是 r(状态 1)。交错式洗牌开始，假设梅花牌先落下(状态 2)，然后是红心(状态 3)、黑桃(状态 4)、又一张梅花(状态 5)。每落下一张牌后，我们检视手中两叠牌的底牌，就可以看到前两张牌落下后，我们从初始状态 r，转换到状态 p，接着又转换为状态 r。接下来落下的两张牌，又会让状态从 r 转换到 s，再转换到 q。

本自动机是确定自动机，因此未来状态并非随机决定。所以在魔术师开始预测时，亮出的每一组两张牌，都对应着自动机上的两条路径(即使一个双周期)。此外，每经过两次转换，自动机不是回到初始状态，就是来到初始状态对角的状态。

由此可得以下结果：

定理一：

    1. 若目前状态位在 {p, s} 对角线上，那么经过两次转换，自动机必然会回到 {p, s} 对角线上的状态； 

    2. 若目前状态位在 {q, r} 对角线上，那么经过两次转换，自动机必然会回到 {q, r} 对角线上的状态；

由定理一可知，两副牌事前排列的牌面特性、颜色规律(即异背组合究竟是红黑、红红，还是黑黑)，在洗牌后都不会改变。请注意，位在 p, s 对角线的状态，两张底牌都是牌面同色；位在 q, r 对角线的状态中，两张底牌花色都是同样强弱。每经过两次转换，自动机不是回到初始状态，就是来到对角的状态，只有颜色与强弱皆相反的组合才是例外(因为这种组合在两种版本中都有)。因此由定理一可知，牌面颜色版本只可能有牌面颜色相同的组合，花色强弱版本只可能有花色强弱相同的组合。这样一来，魔术师就必能预测异背组合的牌面颜色或花色强弱。

---

6. 模式预测型吉尔布雷斯扑克牌魔术变化版：牌面颜色

要用牌背颜色预测牌面颜色，同样可以将交错式洗牌自动机的弧线重新上色，反映每张牌的牌面颜色。以下是牌面颜色与牌背颜色两种自动机：

b. 牌面颜色自动机(左)；d. 牌背颜色自动机(右)

重新提醒读者，两张牌背相同颜色的牌我们定义为「同背组合」，两张牌背颜色相异的牌则定义为「异背组合」。

我们比较图 (d) 与图 (b)，即可观察到相对应的路径颜色有所不同。若希望两个变化版的预测方式保持一致，在进行牌面颜色变化版的前置作业时，就必须确保两张底牌牌面同色。观察可知，这个变化版的初始状态必然是状态 r 或状态 q，且每个双周期开始都必然是这两个状态之一。牌背颜色自动机中每一个颜色相异的双周期，可观察到牌面颜色自动机对应到的都是颜色相同的双周期；牌背颜色自动机中每一个颜色相同的双周期，可观察到牌面颜色自动机对应到的都是颜色相异的双周期。因此，魔术师即可确知，异背组合扑克牌牌面必然颜色相同，同背组合扑克牌牌面必然颜色相异。

另外，牌背颜色自动机中每一个颜色相异的双周期，牌面颜色自动机对应到的双周期是「红红、黑黑」交错出现。请注意，牌背颜色自动机中所有颜色相异的双周期，从状态 r 或状态 q 开始，双周期结束后必定是来到对角 {q, r} 的状态。牌面颜色自动机中，相对应的双周期都是同色的，但红色双周期与黑色双周期是交错出现。从扑克牌魔术的观点来看，这意味着出现异背组合时，牌面颜色必然是「黑黑」与「红红」交错出现。

从以上的推论可知：

定理二：

    1. 图 (d) 中，从状态 r 或状态 q 开始，又回到同一状态的双周期，两条路径颜色相同，图 (b) 中对应的双周期两条路径颜色却相异；

    2. 图 (d) 中，从状态 r 或状态 q 开始，对角状态结束的双周期，两条路径颜色相异，图 (b) 中对应的双周期两条路径颜色却相同；

    3. 假设初始状态 q₀ 位在 {r, q} 对角线上，那么 C = {p₁, p₂, ..., p_m}(即所有异背组合的集合)中牌面颜色将交错出现，意即 p_i 组合的牌面颜色必然与 p_i+1 组合相异。

定理二的前两条，就是本魔术使用的预测方法。透过分析牌背颜色与牌面颜色自动机的颜色差异，我们可以根据本定理推论出一套简单易记的规则：如果一组两张牌的牌背颜色相异，则牌面颜色必定相同，如果两张牌的牌背颜色相同，则牌面颜色(花色)必然相异。本定理第 3 条与前一小节的定理一结合，即会发挥重要角色，确立了异背组合中牌面颜色出现的规律。具体来说，异背组合的牌面颜色，必然与前一个异背组合牌面颜色的相反。此外，本定理也显示表演一开始时的两张底牌(即自动机的初始状态)颜色必须相同。以上即为本变化版的预测方法。

---

7. 模式预测型吉尔布雷斯扑克牌魔术变化版：花色强弱

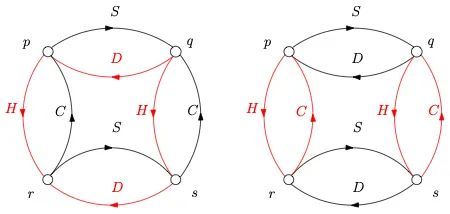
本变化版中，同样须将交错式洗牌自动机的弧线上色，代表每一组牌的花色强弱。本例中，强花色(红心与黑桃)的弧线上红色，弱花色(梅花与方块)的弧线则不上色。以下是花色强弱自动机与牌背颜色自动机：

c. 花色强弱自动机(左)；d. 牌背颜色自动机(右)

观察两个自动机，同样可以利用前节的推论过程，发现所有异背组合的花色强弱都相同，所有同背组合的花色强弱都相异。唯一的差别在于前置作业，在预测花色强弱的版本中，两叠牌的底牌必须颜色相异。经过这样的前置作业，表演的初始状态便会是状态 p 或状态 s。如此一来，每一个双周期都是从初始状态 p 与 s 开始，在同一状态或对角状态结束。

从以上的推论可知：

定理三：

    1. 图 (d) 中，从状态 p 或状态 s 开始，又回到同一状态的双周期，两条路径颜色相同，图 (c) 中对应的双周期两条路径颜色却相异；

    2. 图 (d) 中，从状态 p 或状态 s 开始，对角状态结的双周期，两条路径颜色相异，图 (b) 中对应的双周期两条路径颜色却相同；

    3. 假设初始状态 p₀ 位在 {p, s} 对角线上，那么 C = { p₁, p₂, ..., p_m}(即所有异背组合的集合)中牌面颜色将交错出现，意即 p_i 组合的牌面颜色必然与 p_i+1 组合相异。

与前节同理，定理三让我们设计出此版本魔术的预测方法，方法与前一个版本完全相同，只是预测对象变成花色强弱，而非牌面颜色。我们利用定理三的前两条，可以推论出一套简单易记的规则：如果一组两张牌的牌背颜色相异，则花色强弱必定相同，如果两张牌的牌背颜色相同，则花色强弱必然相异。定理三的第 3 条与定理一结合，同样也能确立异背组合的花色强弱规律，每一个异背组合两张牌的花色都跟前一个异背组合相反。此外，本定理也显示表演一开始时的两张底牌(即自动机的初始状态)颜色必须相异，花色则相同。以上即为本变化版的预测方法。

---

8. 魔术总结

有了以上的自动机，我们就可以利用数学解释本魔术背后的原理。表演开始前，魔术师先准备两副牌背颜色不同的扑克牌，先将两副牌各自用花色分类，然后将两副牌的方块与黑桃牌交错排列、红心与梅花牌交错排列。从自动机的设计来看，牌面颜色变化版魔术初始状态必须在 {q, r} 对角线上，花色强弱变化版初始状态则必须在 {p, s} 对角线上。由观察可知，初始状态 {q, r} 对角线上，意即两张底牌牌面颜色必须相同；初始状态在 {p, s} 对角线上，则意即两张底牌必须花色同强弱，换句话说牌面颜色必须相异。因此，魔术师必须确保颜色交错排列的四叠牌中，有一叠底牌的牌面颜色必须与其他三叠相异。如前文所述，魔术师将两副牌收回盒子中，表演开始时拿出排列看似随机的两副牌，然后找出两副牌中方块与黑桃牌跟梅花与红心牌的交界，以此交界将两副牌各切成两叠──到此步骤为止，都不需要数学。完成切牌后，魔术师每叠牌与另一副牌中花色相反的一叠牌，两叠交错洗牌。(例如，红色牌背的红心与梅花牌，搭配蓝色牌背的方块与梅花牌，两叠交错洗牌。)整个洗牌过程，可以利用牌面颜色、牌背颜色与花色强弱三种自动机的状态转换表示。

魔术师开始表演预测魔术，第一种表演是牌面颜色变化版，洗牌时两叠的底牌分别是梅花与黑桃，因此初始状态是状态 r。不过，魔术师到了这个阶段已经看不到牌面了。

魔术师眼前看见的是牌背颜色不同的「异背组合」。这时魔术师可以采用反向推论。在这之前，魔术师已经知道这副牌的方块、梅花、红心与黑桃张数都相同，所以自动机中每一条路径经过的次数也都会相同。因此在这次表演的例子中，自动机初始状态是 r，每亮出一组梅花与红心的同背组合，从自动机的观点就是经过一个双周期(透过 C 路径转换一次，再透过 H 路径转换一次)，回到 r 状态，那么之后必然会有一组黑桃与方块的同背组合，同样是经过一个双周期(透过 S 路径转换一次，再透过 D 路径转换一次)回到 r 状态。每亮出一组梅花与黑桃的异背组合，即是经过一个双周期(透过 C 路径转换一次，再透过 S 路径转换一次)从状态 r 到状态 q，之后必然会有一组红心与方块的异背组合，同样是经过一个双周期(透过 H 路径转换一次，再透过 D 路径转换一次)从状态 r 到状态 q。

有了以上推论，魔术师就知道洗牌过程结束时，最终状态一定与初始状态相同，因为手中洗过的牌红心、方块、黑桃与梅花张数相等，同背组合与异背组合数目也一定相等。如此一来，他就可以开始反向推论的过程，从最后落下的两张牌开始，在心中画出自动机的转换路径。魔术师知道自动机的最终状态与初始状态相同，就可以根据发出的双周期是同背还异背组合，在心中逆着图上的箭头(因为是反向推论，所以路径方向与图上相反)画出一个双周期的路径，自动机如果不是回到同一状态，就是来到对角的状态 —— 这就是倒数第二个状态。接下来，魔术师运用牌面颜色自动机，套上先前利用最终状态与牌背颜色组合所推论出的路径，就可以预测该组牌的牌面颜色或花色强弱。例子中的初始状态是 r，且手上的牌异背组合数目是偶数，因此魔术师就能推论，最终状态一定也是 r。魔术师看到发出的是异背组合，就沿着图中的箭头相反方向推论，先沿路径 D，再沿路径 H，来到对角的状态 q。观察牌面颜色自动机上对应的路径后，魔术师发现两条对应的路径都是红色，代表洗牌过程落下的最后两张牌都是红色牌，让自动机从状态 q 转换到最终状态 r。因此，魔术师可预测发出第一组异背组合，两张牌都是红色。

发完第一组两张牌后，魔术师拿起下一组两张牌，发现是同背组合。魔术师马上回想自动机，记得同背组合代表的是回到同状态的双周期，不管是从 q 状态或 r 状态开始，都会回到同一个状态。观察心中的牌背颜色自动机，画出回到同一个 q 状态的路径后，魔术师同样快速与牌面颜色自动机比对，发现牌背颜色自动机对应的两条路径代表的是一红一黑的两张牌，这两张牌洗牌时是在最后一组异背组合之前落下的，让自动机停留在状态 q。因此，魔术师可预测这组同背组合，必然是一黑一红。

接下来，魔术师再拿起两张牌，发现又是异背组合。魔术师知道最终状态是 r，所以可以再次利用反向推论，推出这个组合的牌面颜色。因为先前的异背组合代表的是一个将自动机从状态 q 转换为状态 r 的双周期，所以前一个异背组合一定代表着从状态 r 转换为状态 q 的双周期，最后落下的异背组合才能将自动机从状态 q 转换至最终的状态 r。因此，魔术师看到眼前的异背组合，就再次在心中逆着画出从状态 q 到对角状态 r 的双周期路径。与牌面颜色自动机比对后，发现从状态 q 转换为状态 r，会经过两条黑色路径，一条是 S 路径，另一条是标注 C 路径，代表在洗牌时是两张黑色牌落下，构成眼前的组合。

运用同样的推论方法，魔术师只要看到接下来每组牌的牌背颜色，就可以成功预测该组牌的牌面颜色。第一副牌预测完后，第二副牌利用同样的方法，即可成功预测每一组牌的花色强弱。表演完之后魔术师鞠个躬，顺利的话观众应该会起立鼓掌。

这种魔术还可以进一步延伸，牌背颜色可以不止两种，甚至可以利用牌面不止有数字与花色两种性质的卡牌(例如 Uno 游戏的卡牌)。

---

9. 表演秘诀

当然，数学魔术也是一种表演，所以本文最后，提供几个小秘诀，在观众面前表演模式预测型吉尔布雷斯扑克牌魔术时可以用上。

实际表演魔术时，魔术师除非在洗牌前已经牢记底牌是哪两张，否则不可能知道自动机初始状态是哪一个(有两种可能性)，因此我们建议第一组异背组合牌一定要邀请观众猜测。这样不但能让观众更有参与感，而且你为了检查答案，可以看见第一组牌，就知道了自动机的初始状态，如此即可成功预测下一个异背组合的牌面颜色。

在表演过程中，魔术师预测的方式最好尽量多变。可以假装看前一组牌、凝视观众，甚至闻闻扑克牌的味道，让每一次预测都富含趣味与新鲜感。另外在预测时也要故作支吾犹豫，不要让观众看出你的预测是用公式推论出来的。

较有经验的魔术师，可以先假切、假洗几次牌，强化眼前这副牌是随机的假象。建议扑克牌刚从盒子拿出来的时候，就可以假切假洗。

最后，在将一副牌切成事前排列的两叠时，要让观众相信你是随意切个大概，而不是刚好切成两叠 26 张牌。建议可以说类似这样的话：「我们大概把牌切一半，这样看起来差不多，一两张差距没关系。」如此一来观众更无疑心，魔术就会显得更加精采。

只要表演够有气势，即使观众都是专业数学家与魔术师，肯定也看不出破绽！

---

致谢

本文作者衷心感谢我的精神导师：哈佛商业学院的 Scott Duke Kominers 教授。我在哈佛数学科学与应用中心担任经济设计研究员时，教授对我的工作有诸多指导与支持，让我十分难忘。此外，也希望感谢石溪大学的顾险峰教授，让我认识图论与自动机论、宾州大学的余成龙博士帮助我的证明过程、Spelman College 的 Colm Mulcahy 教授、圣本笃学院的 Bret Benesh 教授，以及 Joe M. Turner 先生对我的诸多建议，还有哈佛大学的丘成桐教授带给我的启发。

---

参考资料

[1] Persi Diaconis and Ron Graham, Magical Mathematics: The Mathematical Ideas That Animate Great Magic Tricks, Princeton University Press, 2012.

[2] N.G. de Bruijn, A riffle shuffle card trick and its relation to quasi-crystall theory, Nieuw Archief voor Wiskunde 5 (1978), no. 3, 285--301.

推荐阅读

丘成桐、刘克峰、杨乐、季理真 主编

《数学与人文》丛书第 28 辑

《数学游戏和数学谜题》(副主编 李建华)

欢迎关注《数理人文》杂志微信版

© International Press of Boston

微信订阅号：math_hmat