决策树分类原理(二）27

import numpy as np
from sklearn import tree
import pandas as pd 

加载数据

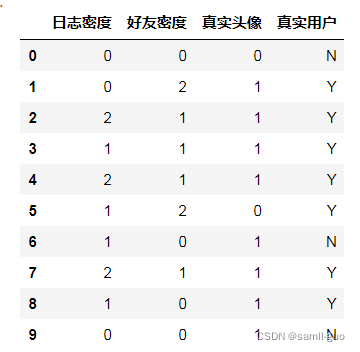
y=np.array(list('NYYYYYNYYN'))
print(y)
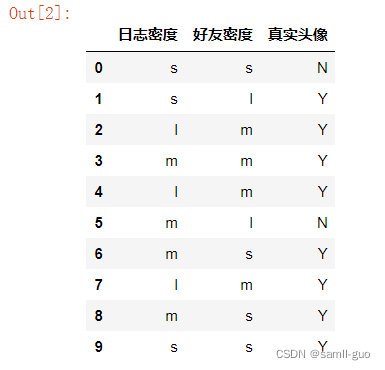
X=pd.DataFrame({'日志密度':list('sslmlmmlms'),
                  '好友密度':list('slmmmlsmss'),
                  '真实头像':list('NYYYYNYYYY')})
X
输出：
['N' 'Y' 'Y' 'Y' 'Y' 'Y' 'N' 'Y' 'Y' 'N']

数据转换
 

#代码只执行一次
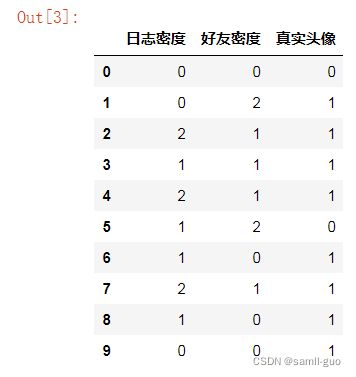
X['日志密度']=X['日志密度'].map({'s':0,'m':1,'l':2})
X['好友密度']=X['好友密度'].map({'s':0,'m':1,'l':2})
X['真实头像']=X['真实头像'].map({'N':0,'Y':1})
X

 建模预测

model=tree.DecisionTreeClassifier(criterion='entropy')#criterion=''分类标准
model.fit(X,y)
model.score(X,y)

对上面决策树进行可视化

import matplotlib.pyplot as plt
# from matplotlib.font_manager import FontManager
# fm=FontManager()
# [font.name for font in fm.ttflist]
#以上是查看所有中文字体的方法

plt.rcParams['font.family']='SimHei'#设置中文字体
plt.figure(figsize=(12,16))
fn=X.columns

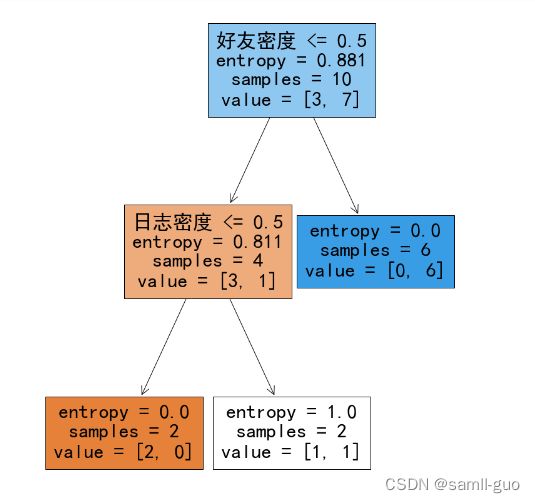
#根据模型绘制决策树
_=tree.plot_tree(model,filled=True,feature_names=fn)
#filled=True表示填充颜色，feature_names=fn表示根据fn进行决策
plt.savefig('./决策树.png',dpi=100)#进行保存

可视化二

import graphviz 
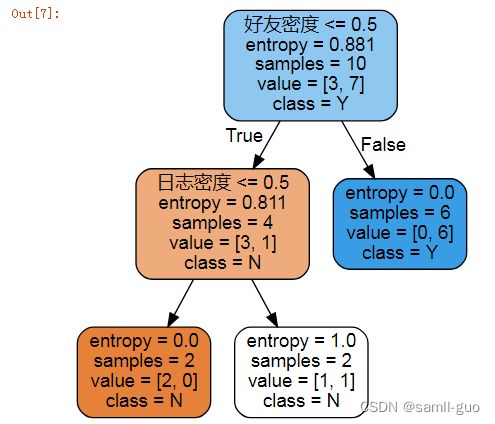
dot_data=tree.export_graphviz(model,filled=True,feature_names=fn,rounded=True,class_names=np.unique(y))
#feature_names=fn特征；rounded==True圆角；class_names=目标值的类别
graph=graphviz.Source(dot_data)
graph

 

graph.render('./决策树2',format='png')
输出：
'决策树2.png'

手动计算决策树到底如何分类的计算未分类的信息熵

 

计算未分类的信息熵

p1=(y=='N').mean()#计算刚开始N的概率
p2=(y=='Y').mean()#计算刚开始Y的概率
print(p1,p2)
输出：
0.3 0.7

 

p1*np.log2(1/p1)+p2*np.log2(1/p2)
输出：
0.8812908992306926

按照日志密度进行划分,求信息熵

X['真实用户']=y
X

#步骤一：分类别
x=X['日志密度'].unique()#计算日志密度的类别
x.sort()#排序
print(x)

#步骤二：依次对类别密度划分，再求相应的裂分值
for i in range(len(x)-1):#三个类别可以两次划分，所以需要减1
    split=x[i:i+2].mean()#通过切割得到两个类别数，计算裂分值。如(0+1)/2和（1+2）/2
    #x[i:i+2]表示依次迭代的获取相邻两个数，然后再求它们的均值
    
    cond=X['日志密度']<=split#会分成两边，要分布计算信息熵
    
    #步骤三：通过上面的cond,计算概率分布(权重)
    p=cond.value_counts()/cond.size#cond.size为总数
    indexs=p.index#要么是True,要么False
    
    entropy=0
    for index in indexs:
        user=X[cond==index]['真实用户']#取出对应值的目标值y的数据
        
        p_user=user.value_counts()/user.size
        #每个分支的信息熵
        entropy+=(p_user*np.log2(1/p_user)).sum()*p[index]
    print(split,entropy)
        
输出：
[0 1 2]
0.5 0.689659695223976
1.5 0.689659695223976

#信息增益
0.881-0.689
输出：
0.19200000000000006