数据结构与算法——堆和堆排序 动画演示
文章目录
- 一、堆和优先队列
-
- 什么是优先队列?
- 优先队列的实现方法
- 二、堆的基本实现
-
- 用数组存储二叉堆
- 向最大堆中添加元素Shift Up
- 向最大堆中取出元素Shift Down
- 三、堆排序和Heapify
-
- 基础堆排序
- 优化的堆排序和Heapify
- 四、原地堆排序
- 五、排序算法总结
- 六、索引堆
-
- 堆的局限性
- 索引堆的基本实现
- 索引堆的优化
- 七、和堆相关的问题
- 附录:
-
- 堆的完整代码:
- 索引堆的完整代码:
一、堆和优先队列
什么是优先队列?
普通队列:先进先出,后进后出
优先队列:出队顺序和入队顺序无关,和优先级有关
动态选择优先级最高的人物执行,优先队列是动态执行的,每次都会更新队列。例如:在N个元素中选择前M个元素,用排序的方法复杂度为NlogN,而使用堆则为NlogM。优先队列的主要操作是:入队,出队(取出游戏那几最高的元素)
优先队列的实现方法
优先队列实现的比较:
| 入队 | 出队 | |
|---|---|---|
| 普通数组 | O(1) | O(n) |
| 顺序数组(排序后的数组) | O(n) | O(1) |
| 堆 | O(lgn) | O(lgn) |
由表可以看出,普通数组实现优先队列入队时直接加入到数组末尾,复杂度为O(1);出队时遍历整个数组,复杂度为O(n)。
顺序数组因为是不断维护有序新的数组,出队直接取出队首即可,复杂度为O(1);而入队时则需要找到入队插入合适的顺序,复杂度为O(n)。
用堆这种数据结构实现优先队列要比另外两种平均复杂度要低一些。
最极端的情况下,对于总共N个请求,使用普通数组挥着书序数组,最差情况:O(n^2),而使用堆:O(nlgn)。
二、堆的基本实现
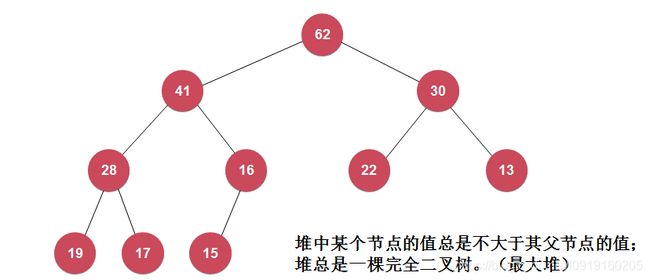
上面说到堆的时间复杂度为O(nlgn),可以想到堆是一个树型结构。最经典的实现就是二叉堆,这个二叉树有两个特点:
1.二叉堆的父节点永远大于两个子节点(最大堆);
2.二叉堆是一个完全二叉树(完全二叉树:除最后一层外,其余层都是满的,最后一层的子节点也都在最左边)。
注意:二叉堆并不意味着层数越高数值越大!
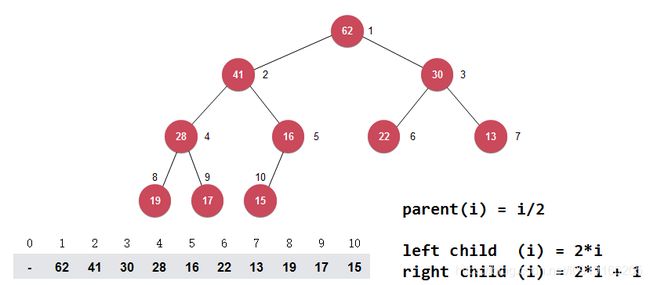
用数组存储二叉堆
因为二叉堆是一个完全二叉树,说以可以用数组来实现。当我们从上到下,从左到右对二叉堆的每一个结点进行编号时可以发现,左结点的序号是父节点的2倍,右节点是父节点序号的2倍+1。可以用如下公式就可以推出左右孩子结点的序号:
首先编写一个堆的骨架,代码如下(c++):
template<typename T>
class MaxHeap{
public:
// 构造函数, 构造一个空堆, 可容纳capacity个元素
MaxHeap(int capacity){
data = new T[capacity+1];//第一个元素不用
count=0;//初始化数量为0
}
//析构函数释放数组
~MaxHeap(){
delete[] data;
}
//获取堆元素的个数
int size(){
return count;
}
//堆是否为空
bool isEmpty(){
return count==0;
}
//获取元素值
T getValue(int index){
return data[index];
}
private:
T* data;
int count;//堆的元素个数
};
向最大堆中添加元素Shift Up
向堆中添加一个元素相当于在数组最后添加一个元素,然后调节新加入元素的位置。
Shift Up操作即新加入的元素不断的和自己的父节点进行比较,如果不符合堆的定义就与父节点进行交换。如下动图所示,最大堆中添加了一个52的结点:
在原代码中添加shiftUp(int k)函数,insert(T item)函数。insert(T item)函数为public,shiftUp(int k)函数为private。
shiftUp(int k)函数主要代码:
void shiftUp(int k){
while( k>1 && data[k/2]<data[k]){
swap(data[k/2],data[k]);
k=k/2;
}
}
insert(T item)函数主要代码(动态添加数组容量,容量增加原来的一半):
//插入元素
void insert(T item){
//动态增加容量,当插入元素超过容量时,容量增加原来的一半
if(count+1>capacity+1){
T* data2=new T[capacity+1];
for(int i=0;i<=count;i++){
data2[i]=data[i];
}
if(capacity==1){
capacity=capacity*2;
}else{
capacity=capacity+capacity/2;
}
data=new T[capacity+1];
for(int i=1;i<=count;i++){
data2[i]=data[i];
}
delete[] data2;
}
//插入元素
data[count+1]=item;
count++;
shiftUp(count);//调整
}
向最大堆中取出元素Shift Down
堆的出队只能取出优先级最大的元素,即根节点的元素。将最后一个元素放到根节点的位置,数量count减一,再将这个元素向下调整。
Shift Down操作即将元素与它的左右孩子比较,当它比左右孩子小时,则与左右结点中较大的进行交换。如下动图所示,最大堆中取出元素:
在原代码中添加shiftDown(int k)函数,extractMax()函数。extractMax()函数为public,shiftDown(int k)函数为private。
shiftDown(int k)函数主要代码:
void shiftDown(int k){
while(2*k<=count){
//左结点小于元素数目
//先比较左右两个结点,确定编号j
int j=k*2;
if(j+1<=count&&data[j+1]>data[j])
j++;
//如果当前结点比左右结点大,则退出循环
if(data[k]>data[j])
break;
//否则data[k]和data[j]交换位置
swap(data[k],data[j]);//(交换函数可以做优化,改成赋值的形式,具体见排序那篇博客)
k=j;
}
}
extractMax()函数主要代码:
// 从最大堆中取出堆顶元素, 即堆中所存储的最大数据
T extractMax(){
assert( count > 0 );//元素数目要大于0
T ret=data[1];//要取出的数
swap(data[1],data[count])//和最后一个元素交换(交换操作可以改成赋值操作)
count--;
shiftDown(1);
return ret;
}
三、堆排序和Heapify
基础堆排序
实现堆排序可以将数组的元素全部插入到中,再将堆中的元素全部重新取出放入数组中即得到有序的队列。
无论是创建堆的过程, 还是从堆中依次取出元素的过程, 时间复杂度均为O(nlogn)。整个堆排序的整体时间复杂度为O(nlogn)。
template<typename T>
void heapSort1(T arr[], int n){
MaxHeap<T> maxheap = MaxHeap<T>(n);
for( int i = 0 ; i < n ; i ++ )
maxheap.insert(arr[i]);
for( int i = n-1 ; i >= 0 ; i-- )
arr[i] = maxheap.extractMax();
}
优化的堆排序和Heapify
将整个数组构建成一个堆有更好的方式,将一个数组构造成一个堆的过程叫做Heapify。
假设有如下图所示的数组,这个数组自动形成了一个二叉树,但还不是二叉堆。可以观察得到:
1.每一个叶子结点都构成一个堆(因为只有一个元素);
2.第一个非叶子结点序号为总数count / 2(如下图所示,第一个非叶子结点序号为10/2=5)。
Heapify的过程,从后向前的依次讨论不是叶子的结点,对它们依次进行Shift Down操作,使以改结点为根节点的二叉树为一个二叉堆。动画演示如下:
堆中重新编写一个构造函数,构造函数代码如下:
// 构造函数, 通过一个给定数组创建一个最大堆
// 该构造堆的过程, 时间复杂度为O(n)
MaxHeap(T arr[], int n){
data = new T[n+1];
capacity=n;
//数组的值赋值到data中
for(int i=0;i<n;i++){
data[i+1]=arr[i];
}
count=n;
for(int i=count/2;i>=1;i--){
shiftDown(i);
}
}
重新编写堆排序的函数,heapSort2借助我们的heapify过程创建堆。
此时, 创建堆的过程时间复杂度为O(n), 将所有元素依次从堆中取出来, 实践复杂度为O(nlogn)。
堆排序的总体时间复杂度依然是O(nlogn), 但是比上述heapSort1性能更优, 因为创建堆的性能更优。heapSort2代码如下:
template<typename T>
void heapSort2(T arr[], int n){
MaxHeap<T> maxheap = MaxHeap<T>(arr,n);
for( int i = n-1 ; i >= 0 ; i-- )
arr[i] = maxheap.extractMax();
}
heapSort1的效率要比heapSort2的效率低,堆排序的效率还是不如归并排序和快速排序。
结论:将n个元素逐个插入到一个空堆中,算法复杂度是O(nlogn),而Heapify的过程算法复杂度为O(n)。
四、原地堆排序
之前说到的堆排序是将数组依次插入到堆中进行排序,整个过程又额外增加了n个空间,而实际上排序过程完全可以在原地进行,不需要额外的空间。
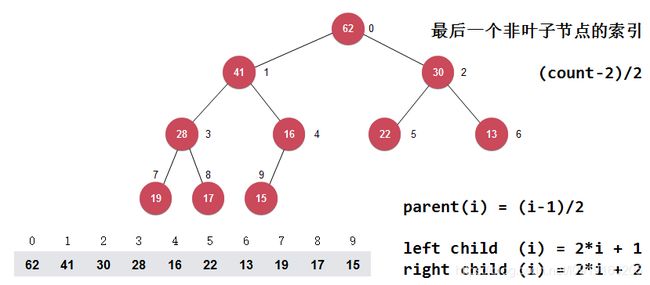
具体步骤:一个数组可以看成一个完全二叉树
步骤一:先通过Heapify的过程构造成一个堆,设构造后的堆第一个元素是v,v即是最大的元素,设最后一个元素为w,将v和w交换,此时蓝色的区域是排序的部分,橙色的部分便不满足二叉堆。
步骤二:对橙色部分进行Shift Down操作使之变成一个二叉堆,此时该部分变成红色,继续执行步骤一。
执行步骤如下图所示:
二叉堆的序号变成从0开始,最后一个飞叶子结点的索引为(count-2)/2,使用的索引公式如下图所示:
原地堆排序heapSort3实现代码如下:
// n:数组元素个数,k:对第k个元素进行shiftDown
// 相对于shiftDown()只是索引从0开始了
template<typename T>
void shiftDown2(T arr[], int n, int k){
while(2*k+1<=n){
//左结点小于元素数目
//先比较左右两个结点,确定编号j
int j=k*2+1;
if(j+1<n&&arr[j+1]>arr[j])
j++;
//如果当前结点比左右结点大,则退出循环
if(arr[k]>arr[j])
break;
//否则data[k]和data[j]交换位置
swap(arr[k],arr[j]);
k=j;
}
}
// 不使用一个额外的最大堆, 直接在原数组上进行原地的堆排序
template<typename T>
void heapSort3(T arr[], int n){
// 注意,此时我们的堆是从0开始索引的
// 从(最后一个元素的索引-1)/2开始
// 最后一个元素的索引 = n-1
for(int i=(n-2)/2;i>=0;i--){
// Heapify的过程构造成一个堆
shiftDown2(arr, n, i);
}
for(int i=n-1;i>0;i--){
swap(arr[0],arr[i]);
shiftDown2(arr, i, 0);
}
}
五、排序算法总结
| 平均时间复杂度 | 原地排序 | 额外空间 | 稳定排序 | |
|---|---|---|---|---|
| 插入排序 | O(n^2) | √ | O(1) | √ |
| 归并排序 | O(nlogn) | ╳ | O(n) | √ |
| 快速排序 | O(nlogn) | √ | O(logn) | ╳ |
| 堆排序 | O(nlogn) | √ | O(1) | ╳ |
排序算法的稳定性
稳定排序:对于相等元素,排序后,原来靠前的元素依然靠前。即相等元素的相对位置没有发生变化。如图所示:

插入排序是稳定的,是因为元素在和前一个元素比较时,当与前一个元素相等时就不进行交换了。动画演示如下图:
归并排序是稳定的,是因为元素在比较时,如果遇到相同的元素,就先和左边的元素替换。如下图所示,左右的元素3是相同的,先替换左边的3。动画演示如下图:
六、索引堆
堆的局限性
1.在一般的堆中,需要经常交换两个元素。如果元素十分复杂,比如每个位置上存的是一篇10万字的文章。那么交换它们的位置将产生大量的时间消耗。
2.由于我们的数组元素的位置在构建成堆之后发生了改变,那么我们之后就很难索引到它,很难去改变它。例如我们在构建成堆后,想去改变一个原来元素的优先级(值),将会变得非常困难。
3.可能我们在每一个元素上再加上一个属性来表示原来位置可以解决,但是这样的话,我们必须将这个数组遍历一下才能解决。(性能低效)
于是就有了索引堆的概念。
索引堆的基本实现
将数据和索引分开存储,真正构建堆的是由索引构成的。如下图所示,圆圈里存的是索引号:
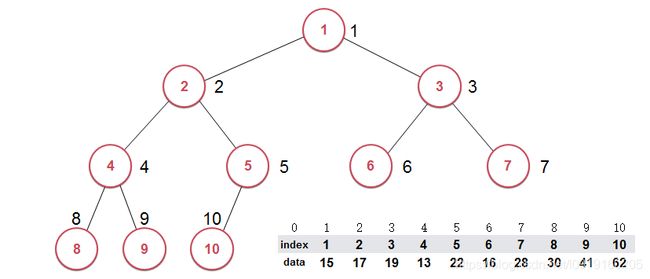
当数组变成堆时,就变成了如下图所示:
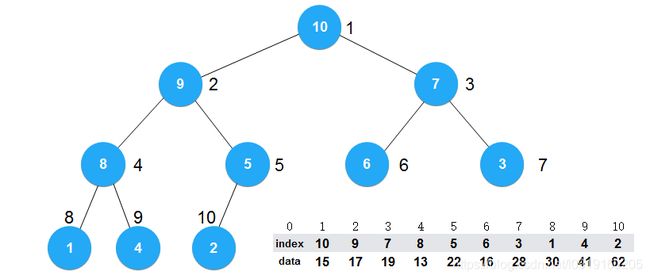
数组对应的数据data没有改变,改变的是索引index的值。上图index的顺序就是堆的顺序,堆的元素索引为10,对应的元素值为62,以此类推。
索引堆的两大重要特点
1 比较的是真实元素的大小,交换的是对应的索引index的位置,真实的data数组并没有任何改变。数据和索引是分开存储的,这意味着索引数组是连续的,数据数组可以不连续。这一点我想了好久才明白(汗。。。)
2 访问数据元素,必须先找到其索引,即先找到index[]的值
注意:data[]数组我们是从1开始存储的,但是真实的索引是从0开始的
索引堆在图论算法中求最短路径以及最小生成树中都有应用。
相对于基本堆的实现,索引堆比它多了索引数组
int *indexes; // 最大索引堆中的索引数组
相应的构造函数和析构函数对索引数组进行初始化:
// 构造函数, 构造一个空的索引堆, 可容纳capacity个元素
IndexMaxHeap(int capacity){
data = new Item[capacity+1];
indexes = new int[capacity+1];
count = 0;
this->capacity = capacity;
}
~IndexMaxHeap(){
delete[] data;
delete[] indexes;
}
插入函数:(数据和索引是分开存储的,这意味着索引数组是连续的,数据数组可以不连续)
// 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
void shiftUp( int k ){
//先拿到索引,再比较索引对应的数据
while( k > 1 && data[indexes[k/2]] < data[indexes[k]] ){
swap( indexes[k/2] , indexes[k] );
k /= 2;
}
}
// 向最大索引堆中插入一个新的元素, 新元素的索引为i, 元素为item
// 传入的i对用户而言,是从0索引的
void insert(int i, T item){
assert( count + 1 <= capacity );
assert( i + 1 >= 1 && i + 1 <= capacity );
i += 1;//从1开始索引
data[i] = item;//数据数组可能不是连续的
indexes[count+1] = i;//索引数组是连续的
count++;
shiftUp(count);
}
取出元素:
// 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
void shiftDown( int k ){
while( 2*k <= count ){
int j = 2*k;
if( j + 1 <= count && data[indexes[j+1]] > data[indexes[j]] )
j += 1;
if( data[indexes[k]] >= data[indexes[j]] )
break;
swap( indexes[k] , indexes[j] );
k = j;
}
}
// 从最大索引堆中取出堆顶元素, 即索引堆中所存储的最大数据
T extractMax(){
assert( count > 0 );
T ret = data[indexes[1]];//找到索引对应的值
swap( indexes[1] , indexes[count] );//将索引交换
count--;
shiftDown(1);
return ret;
}
最大索引堆的一些特殊操作:
取出最大元素的索引:
// 从最大索引堆中取出堆顶元素的索引
int extractMaxIndex(){
assert( count > 0 );
int ret = indexes[1] - 1;// 对用户而言,是从0索引的
swap( indexes[1] , indexes[count] );
count--;
shiftDown(1);
return ret;
}
将最大索引堆中索引为i的元素修改为newItem,修改后元素先找到其在堆中对应的位置,再先后进行shiftUp和shiftDown操作,代码如下:
// 将最大索引堆中索引为i的元素修改为newItem
void change( int i , T newItem ){
i += 1;//索引堆是从1开始的
data[i] = newItem;
// 找到indexes[j] = i, j表示data[i]在堆中的位置
// 之后shiftUp(j), 再shiftDown(j)
for( int j = 1 ; j <= count ; j ++ )//遍历整个索引数组,找到data[i]在堆中的位置j
if( indexes[j] == i ){
shiftUp(j);
shiftDown(j);
return;
}
}
索引堆的优化
上面将最大索引堆中索引为i的元素修改为newItem的过程中,重新维护index数组时是遍历整个index数组找到该索引在堆中的位置。
其实可以用反向查找的思路,单独设置一个rev数组来存放索引在堆中的位置。如下图所示,索引1在堆中的位置就是8,以此类推:

rev数组和index数组之间的关系如下图所示:

在原来索引堆中添加反向索引数组:
int *reverse; // 最大索引堆中的反向索引, reverse[i] = x 表示索引i在x的位置
相应的构造函数和析构函数修改:
// 构造函数, 构造一个空的索引堆, 可容纳capacity个元素
IndexMaxHeap(int capacity){
data = new Item[capacity+1];
indexes = new int[capacity+1];
reverse = new int[capacity+1];
for( int i = 0 ; i <= capacity ; i ++ )
reverse[i] = 0;//堆从索引为1开始,所以初始化为0是表示不存在
count = 0;
this->capacity = capacity;
}
~IndexMaxHeap(){
delete[] data;
delete[] indexes;
delete[] reverse;
}
插入函数:
// 向最大索引堆中插入一个新的元素, 新元素的索引为i, 元素为item
// 传入的i对用户而言,是从0索引的
void insert(int i, Item item){
assert( count + 1 <= capacity );
assert( i + 1 >= 1 && i + 1 <= capacity );
// 再插入一个新元素前,还需要保证索引i所在的位置是没有元素的。
assert( !contain(i) );
i += 1;
data[i] = item;
indexes[count+1] = i;
reverse[i] = count+1;
count++;
shiftUp(count);
}
取出元素对应的代码如下:
// 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
void shiftDown( int k ){
while( 2*k <= count ){
int j = 2*k;
if( j + 1 <= count && data[indexes[j+1]] > data[indexes[j]] )
j += 1;
if( data[indexes[k]] >= data[indexes[j]] )
break;
swap( indexes[k] , indexes[j] );
reverse[indexes[k]] = k;
reverse[indexes[j]] = j;
k = j;
}
}
// 从最大索引堆中取出
堆顶元素, 即索引堆中所存储的最大数据
Item extractMax(){
assert( count > 0 );
Item ret = data[indexes[1]];
swap( indexes[1] , indexes[count] );
reverse[indexes[count]] = 0;
reverse[indexes[1]] = 1;
count--;
shiftDown(1);
return ret;
}
将最大索引堆中索引为i的元素修改为newItem,change函数如下:
// 看索引i所在的位置是否存在元素
bool contain( int i ){
assert( i + 1 >= 1 && i + 1 <= capacity );
return reverse[i+1] != 0;
}
// 将最大索引堆中索引为i的元素修改为newItem
void change( int i , Item newItem ){
assert( contain(i) );
i += 1;
data[i] = newItem;
// 找到indexes[j] = i, j表示data[i]在堆中的位置
// 之后shiftUp(j), 再shiftDown(j)
// for( int j = 1 ; j <= count ; j ++ )
// if( indexes[j] == i ){
// shiftUp(j);
// shiftDown(j);
// return;
// }
// 有了 reverse 之后,
// 我们可以非常简单的通过reverse直接定位索引i在indexes中的位置
shiftUp( reverse[i] );
shiftDown( reverse[i] );
}
七、和堆相关的问题
回到之前说的那几个问题,操作系统中可以使用堆实现动态选择优先级最高的任务执行,当有新任务加入时就把其加入到堆中。
在10000个元素中找到前100个元素,可以将这10000个元素依次插入到容量为100的最小堆中,当放满元素后,每插入一个元素,将最小的元素出队,这样遍历完10000个元素后,堆中的元素就是前100的元素。
以后要解决的问题:多路归并排序,最大最小队列(同时得到最大值和最小值)(同时拥有一个最大堆和一个最小堆),二项堆,斐波那契堆???
附录:
堆的完整代码:
template<typename T>
class MaxHeap{
private:
T* data;
int count;//堆的元素个数
int capacity;
void shiftUp(int k){
while( k>1 && data[k/2]<data[k]){
swap(data[k/2],data[k]);
k=k/2;
}
}
void shiftDown(int k){
while(2*k<=count){
//左结点小于元素数目
//先比较左右两个结点,确定编号j
int j=k*2;
if(j+1<=count&&data[j+1]>data[j])
j++;
//如果当前结点比左右结点大,则退出循环
if(data[k]>data[j])
break;
//否则data[k]和data[j]交换位置
swap(data[k],data[j]);
k=j;
}
}
public:
// 构造函数, 构造一个空堆, 可容纳capacity个元素
MaxHeap(int capacity){
data = new T[capacity+1];//第一个元素不用
count=0;//初始化数量为0
this->capacity = capacity;
}
// 构造函数, 通过一个给定数组创建一个最大堆
// 该构造堆的过程, 时间复杂度为O(n)
MaxHeap(T arr[], int n){
data = new T[n+1];
capacity=n;
//数组的值赋值到data中
for(int i=0;i<n;i++){
data[i+1]=arr[i];
}
count=n;
for(int i=count/2;i>=1;i--){
shiftDown(i);
}
}
//析构函数释放数组
~MaxHeap(){
delete[] data;
}
//获取堆元素的个数
int size(){
return count;
}
//堆是否为空
bool isEmpty(){
return count==0;
}
//获取元素值
T getValue(int index){
return data[index];
}
//插入元素
void insert(T item){
//动态增加容量,当插入元素超过容量时,容量增加原来的一半
if(count+1>capacity+1){
T* data2=new T[capacity+1];
for(int i=0;i<=count;i++){
data2[i]=data[i];
}
if(capacity==1){
capacity=capacity*2;
}else{
capacity=capacity+capacity/2;
}
data=new T[capacity+1];
for(int i=1;i<=count;i++){
data2[i]=data[i];
}
delete[] data2;
}
//插入元素
data[count+1]=item;
count++;
shiftUp(count);//调整位置
}
// 从最大堆中取出堆顶元素, 即堆中所存储的最大数据
T extractMax(){
assert( count > 0 );//元素数目要大于0
T ret=data[1];//要取出的数
swap(data[1],data[count]);
count--;
shiftDown(1);
return ret;
}
};
heapSort1(T arr[], int n):
template<typename T>
void heapSort1(T arr[], int n){
MaxHeap<T> maxheap = MaxHeap<T>(n);
for( int i = 0 ; i < n ; i ++ )
maxheap.insert(arr[i]);
for( int i = n-1 ; i >= 0 ; i-- )
arr[i] = maxheap.extractMax();
}
heapSort2(T arr[], int n):
template<typename T>
void heapSort2(T arr[], int n){
MaxHeap<T> maxheap = MaxHeap<T>(arr,n);
for( int i = n-1 ; i >= 0 ; i-- )
arr[i] = maxheap.extractMax();
}
heapSort3(T arr[], int n):
// n:数组元素个数,k:对第k个元素进行shiftDown
// 相对于shiftDown()只是索引从0开始了
template<typename T>
void shiftDown2(T arr[], int n, int k){
while(2*k+1<=n){
//左结点小于元素数目
//先比较左右两个结点,确定编号j
int j=k*2+1;
if(j+1<n&&arr[j+1]>arr[j])
j++;
//如果当前结点比左右结点大,则退出循环
if(arr[k]>arr[j])
break;
//否则data[k]和data[j]交换位置
swap(arr[k],arr[j]);
k=j;
}
}
// 不使用一个额外的最大堆, 直接在原数组上进行原地的堆排序
template<typename T>
void heapSort3(T arr[], int n){
// 注意,此时我们的堆是从0开始索引的
// 从(最后一个元素的索引-1)/2开始
// 最后一个元素的索引 = n-1
for(int i=(n-2)/2;i>=0;i--){
// Heapify的过程构造成一个堆
shiftDown2(arr, n, i);
}
for(int i=n-1;i>0;i--){
swap(arr[0],arr[i]);
shiftDown2(arr, i, 0);
}
}
索引堆的完整代码:
// 最大索引堆
template<typename Item>
class IndexMaxHeap{
private:
Item *data; // 最大索引堆中的数据
int *indexes; // 最大索引堆中的索引, indexes[x] = i 表示索引i在x的位置
int *reverse; // 最大索引堆中的反向索引, reverse[i] = x 表示索引i在x的位置
int count;
int capacity;
// 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
void shiftUp( int k ){
while( k > 1 && data[indexes[k/2]] < data[indexes[k]] ){
swap( indexes[k/2] , indexes[k] );
reverse[indexes[k/2]] = k/2;
reverse[indexes[k]] = k;
k /= 2;
}
}
// 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
void shiftDown( int k ){
while( 2*k <= count ){
int j = 2*k;
if( j + 1 <= count && data[indexes[j+1]] > data[indexes[j]] )
j += 1;
if( data[indexes[k]] >= data[indexes[j]] )
break;
swap( indexes[k] , indexes[j] );
reverse[indexes[k]] = k;
reverse[indexes[j]] = j;
k = j;
}
}
public:
// 构造函数, 构造一个空的索引堆, 可容纳capacity个元素
IndexMaxHeap(int capacity){
data = new Item[capacity+1];
indexes = new int[capacity+1];
reverse = new int[capacity+1];
for( int i = 0 ; i <= capacity ; i ++ )
reverse[i] = 0;
count = 0;
this->capacity = capacity;
}
~IndexMaxHeap(){
delete[] data;
delete[] indexes;
delete[] reverse;
}
// 返回索引堆中的元素个数
int size(){
return count;
}
// 返回一个布尔值, 表示索引堆中是否为空
bool isEmpty(){
return count == 0;
}
// 向最大索引堆中插入一个新的元素, 新元素的索引为i, 元素为item
// 传入的i对用户而言,是从0索引的
void insert(int i, Item item){
assert( count + 1 <= capacity );
assert( i + 1 >= 1 && i + 1 <= capacity );
// 再插入一个新元素前,还需要保证索引i所在的位置是没有元素的。
assert( !contain(i) );
i += 1;
data[i] = item;
indexes[count+1] = i;
reverse[i] = count+1;
count++;
shiftUp(count);
}
// 从最大索引堆中取出堆顶元素, 即索引堆中所存储的最大数据
Item extractMax(){
assert( count > 0 );
Item ret = data[indexes[1]];
swap( indexes[1] , indexes[count] );
reverse[indexes[count]] = 0;
reverse[indexes[1]] = 1;
count--;
shiftDown(1);
return ret;
}
// 从最大索引堆中取出堆顶元素的索引
int extractMaxIndex(){
assert( count > 0 );
int ret = indexes[1] - 1;
swap( indexes[1] , indexes[count] );
reverse[indexes[count]] = 0;
reverse[indexes[1]] = 1;
count--;
shiftDown(1);
return ret;
}
// 获取最大索引堆中的堆顶元素
Item getMax(){
assert( count > 0 );
return data[indexes[1]];
}
// 获取最大索引堆中的堆顶元素的索引
int getMaxIndex(){
assert( count > 0 );
return indexes[1]-1;
}
// 看索引i所在的位置是否存在元素
bool contain( int i ){
assert( i + 1 >= 1 && i + 1 <= capacity );
return reverse[i+1] != 0;
}
// 获取最大索引堆中索引为i的元素
Item getItem( int i ){
assert( contain(i) );
return data[i+1];
}
// 将最大索引堆中索引为i的元素修改为newItem
void change( int i , Item newItem ){
assert( contain(i) );
i += 1;
data[i] = newItem;
// 找到indexes[j] = i, j表示data[i]在堆中的位置
// 之后shiftUp(j), 再shiftDown(j)
// for( int j = 1 ; j <= count ; j ++ )
// if( indexes[j] == i ){
// shiftUp(j);
// shiftDown(j);
// return;
// }
// 有了 reverse 之后,
// 我们可以非常简单的通过reverse直接定位索引i在indexes中的位置
shiftUp( reverse[i] );
shiftDown( reverse[i] );
}
};