汉诺塔问题

汉诺塔的来源

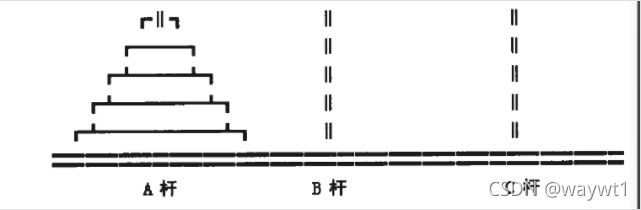
       相传在古印度圣庙中，有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上，有三根杆(编号A、B、C)，在A杆自下而上、由大到小按顺序放置64个金盘。游戏的目标：把A杆上的金盘全部移到C杆上，并仍保持原有顺序叠好。操作规则：每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上，操作过程中盘子可以置于A、B、C任一杆上。

汉诺塔问题递归化

我们给定n个盘子，

当n = 1时，仅需将A杆上的盘子移到C杆上，即 A->C。

当n = 2时，需要将A杆上第一个盘子移到B杆，再将A杆上第二个盘子移到C杆，最后将B杆上的盘子移到C杆，即 A->B,A->C,B->C。

当 n = 3时，移动过程为 A->C  A->B  C->B  A->C  B->A  B->C  A->C。

. . . . . .

在移动过程中我们不难发现，整个移动过程分为三个大步骤即可，当A杆上有n个盘子时：

1.将A杆上从上至下的n-1个盘子移到B杆。

2.将A杆上所剩的最大一个盘子移到C杆。

3.将B杆上的n-1个盘子移到C杆。

同样的道理，当我们需要将n-1个盘子移到B杆上时，同样也分为三个大步骤：

1.将A杆上从上至下的n-2个盘子移到C杆。

2.将A杆上从下至上的第二个盘子移到B杆。

3.将C杆上的n-2个盘子移到B杆。

. . . . . .

由于每个步骤的基本思想相同，便可用函数递归的方法解决此问题。

C语言解决汉诺塔

首先，我们给定主函数框架，

int main()
{
	Hanoi(64, 'A', 'B', 'C');
	return 0;
}

然后，我们给定解决汉诺塔问题的函数Hanoi，

void Hanoi(int n, char pos1, char pos2, char pos3)

这里n代表盘子的个数，pos1代表起始位置，pos2代表中转位置，pos3代表目的位置，由于不需要返回值，故给定其类型为void。

接着，我们给定移动函数move，

void move(char pos1, char pos2)
{
	printf(" %c->%c ", pos1, pos2);
}

目的时打印移动过程中的每一个步骤。

Hanoi函数实现

显然，当n = 1时，只需移动一步，即A->C。

    if (n == 1)
	{
		move(pos1, pos3);
	}

当 n 不为1时，三个大步骤的实现分别为：

1.将n-1个盘子从起始位置A杆通过中转位置C杆移到目的位置B杆：

Hanoi(n - 1, pos1, pos3, pos2);

2.将所剩的一个盘子直接从起始位置A杆移到目的位置C杆：

move(pos1, pos3);

3.将n-1个盘子从起始位置B杆通过中转位置A杆移到目的位置C杆：

Hanoi(n - 1, pos2, pos1, pos3);

将上述步骤完成后，Hanoi函数已经被我们成功实现：

void Hanoi(int n, char pos1, char pos2, char pos3)
{
	if (n == 1)
	{
		move(pos1, pos3);
	}
	else
	{
		Hanoi(n - 1, pos1, pos3, pos2);
		move(pos1, pos3);
		Hanoi(n - 1, pos2, pos1, pos3);
	}
}

解决汉诺塔问题的所有代码为：

#include 

void move(char pos1, char pos2)
{
	printf(" %c->%c ", pos1, pos2);
}

//n:代表盘子的个数
//pos1:起始位置
//pos2:中转位置
//pos3:目的位置

void Hanoi(int n, char pos1, char pos2, char pos3)
{
	if (n == 1)
	{
		move(pos1, pos3);
	}
	else
	{
		Hanoi(n - 1, pos1, pos3, pos2);
		move(pos1, pos3);
		Hanoi(n - 1, pos2, pos1, pos3);
	}
}

int main()
{
	Hanoi(64, 'A', 'B', 'C');
	return 0;
}