并查集

并查集分为一般的并查集和带权并查集
先介绍一般的并查集，何为并查集，和它的名字一样，有并和查俩种功能，是一个集合，假如有5个集合，这5个集合分别是{1} {2} {3} {4} {5}，每个集合中只有一个元素，如果说，将1和2合并成一个集合，那就有{1，2}了，若又说将1,3合并成一个集合，那就有{1，2，3}了，查功能，就是查这俩个元素是不是在同一个集合，比如{1，2，3} {4} {5} ，查1,2 便是同一个集合中，4和5便不在同一个集合中。那么知道大概思路了，怎么用代码来显现出来呢？
大家可能都学过树结构

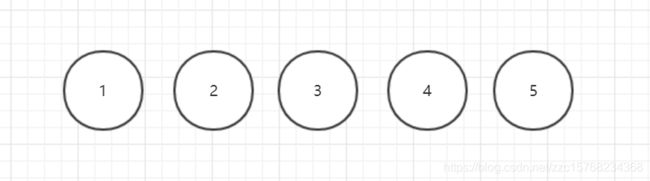
一开始每个元素独自为一个集合

若此时有操作并，将1并入2，1,2便为同一个集合，则有

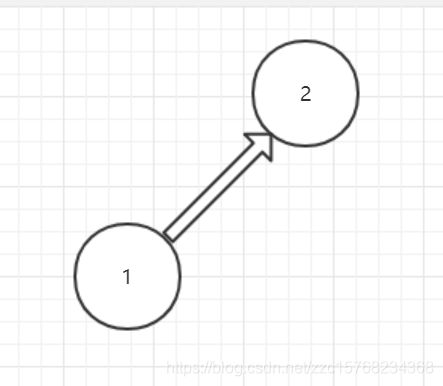
此时就是并操作了
我先给出一串代码

#include
#include
using namespace std;
int a[1005];
int find(int k){
     
	if(a[k]==k) return k;
	return a[k]=find(a[k]);
}
int main(){
     
	int n;
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		a[i]=i;
	return 0;
} 

代码中for(int i=1;i<=n;i++) a[i]=i;
让每一个元素都单独为一个集合，即上面图的5个球
函数find便是找到树的根结点

我们可通过一道题来理解并查集

H - 畅通工程 HDU - 1232
某省调查城镇交通状况，得到现有城镇道路统计表，表中列出了每条道路直接连通的城镇。省政府“畅通工程”的目标是使全省任何两个城镇间都可以实现交通（但不一定有直接的道路相连，只要互相间接通过道路可达即可）。问最少还需要建设多少条道路？

input
测试输入包含若干测试用例。每个测试用例的第1行给出两个正整数，分别是城镇数目N ( < 1000 )和道路数目M；随后的M行对应M条道路，每行给出一对正整数，分别是该条道路直接连通的两个城镇的编号。为简单起见，城镇从1到N编号。
注意:两个城市之间可以有多条道路相通,也就是说
3 3
1 2
1 2
2 1
这种输入也是合法的
当N为0时，输入结束，该用例不被处理。

output
对每个测试用例，在1行里输出最少还需要建设的道路数目。

Sample Input
4 2
1 3
4 3
3 3
1 2
1 3
2 3
5 2
1 2
3 5
999 0
0

Sample Output
1
0
2
998

从题目中我们可以知道n个城镇，若城镇1和城镇2想通，2和3相通，那么1和3便相通，这就是并查集的题目，即1，2，3为同一个集合中，合并完所有城镇后，遍历一遍有多少个集合，即有多少个圈圈，就需要k-1条路来想通
代码如下
代码中的find函数其实算是一个路径压缩函数
比如有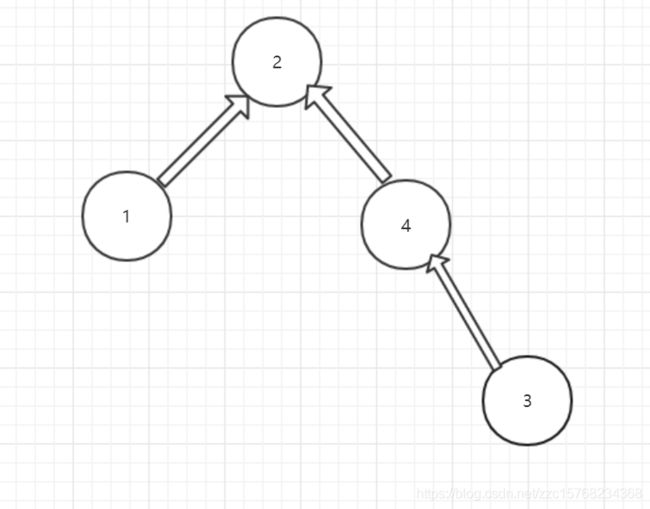
find（3）会先找到4，再找到2，然后逐步返回赋值，最后变为

find函数就是一个找树中根结点，并不断进行路径压缩的过程，最后返回根结点

理解了find函数，那我们就可以看看并过程了
a[find(y)]=find(x);
find(y);

找到x 的根节点赋值给y的根节点，画画图便可清楚的理解了
至于在这里我为什么写了一个find（y），这是进行路径压缩操作，不写也没关系，也可以过，看题目要求咯

#include
#include
using namespace std;
int a[1010];
int find(int x){
     
	if(a[x]==x) return x;
	return a[x]=find(a[x]);
}
int main(){
     
	int n,m;
	int x,y;
	while(scanf("%d",&n)&&n!=0){
     
		int ans=0;
		scanf("%d",&m);
		for(int i=1;i<=n;i++)
			a[i]=i;
		for(int i=0;i<m;i++){
     
			scanf("%d%d",&x,&y);
			a[find(y)]=find(x);
			find(y);
		}
		for(int i=1;i<=n;i++){
     
			if(a[i]==i) ++ans;
		}
		printf("%d\n",ans-1);
	}
}

理解完一般并查集，去巩固一下吧
https://vjudge.net/article/752
前3道都是一般并查集

带权并查集大家可以看看这个大佬的博客，有带权并查集的详细解释

https://blog.csdn.net/yjr3426619/article/details/82315133