[XJTUSE 算法设计与分析] 第六章 分支限界法
文章目录
- 第六章 分支限界法
-
- 6.1 分支限界法的基本思想
-
- 分支限界法和回溯法
- 基本思想
- 示例
-
- 队列式分支限界法
- 优先队列式
- 6.2 单源最短路径问题
-
- 问题描述
- 算法思想
- 实例说明
- 算法设计
- 6.3 0-1背包问题[重点]
-
- 问题描述
- 算法的思想
- 步骤
- 样例
- 核心代码
-
- 上界函数
- 结点定义
- 0-1背包问题优先队列分支限界搜索算法
- 6.4 作业分配问题【重点】
-
- 1、问题描述
- 2、思想方法
- 3、下界的确认
- 4、算法实现步骤
-
-
- 5、实现代码
-
第六章 分支限界法
6.1 分支限界法的基本思想
分支限界法和回溯法
求解目标:回溯法的求解目标是找出解空间树中满足约束条件的所有解,而分支限界法的求解目标则是找出满足约束条件的一个解,或是在满足约束条件的解中找出在某种意义下的最优解。
搜索方式的不同:回溯法以深度优先的方式搜索解空间树,而分支限界法则以广度优先或以最小耗费优先的方式搜索解空间树。
在分支限界法中,每一个活结点只有一次机会成为扩展结点。活结点一旦成为扩展结点,就一次性产生其所有儿子结点。在这些儿子结点中,导致不可行解或导致非最优解的儿子结点被舍弃,其余儿子结点被加入活结点表中。此后,从活结点表中取下一结点成为当前扩展结点,并重复上述结点扩展过程。这个过程一直持续到找到所需的解或活结点表为空时为止。
选择下一个E结点的方法如下:
1)先进先出(FIFO):从活结点表中取出结点的顺序与加入结点的顺序相同。
后进先出(LIFO):从活结点表中取出结点的顺序与加入结点的顺序相反
2)优先队列式分支限界法
按照优先队列中规定的优先级选取优先级最高的节点成为当前扩展节点。
基本思想
1️⃣ 在 e_结点估算沿着它的各儿子结点搜索时,目标函数可能取得的“界”,
2️⃣ 把儿子结点和目标函数可能取得的“界”,保存在优先队列或堆中,
3️⃣ 从队列或堆中选取“界”最大或最小的结点向下搜索,直到叶子结点,
4️⃣ 若叶子结点的目标函数的值,是结点表中的最大值或最小值,则沿叶子结点到根结点的路径所确定的解,就是问题的最优解,否则转 3 继续搜索
示例
0-1背包问题
考虑实例n=4,w=[3,5,2,1],v=[9,10,7,4],C=7。
定义问题的解空间
该实例的解空间为(x1,x2,x3,x4),xi=0或1(i=1,2,3,4)。
确定问题的解空间组织结构
该实例的解空间是一棵子集树,深度为4。
搜索解空间
约束条件
限界条件 cp+rp>bestp
队列式分支限界法
cp初始值为0;rp初始值为所有物品的价值之和;bestp表示当前最优解,初始值为0。
当cp>bestp时,更新bestp为cp。
优先队列式
优先级:活结点代表的部分解所描述的装入背包的物品价值上界,该价值上界越大,优先级越高。活结点的价值上界up=cp+r‘p。
约束条件:同队列式
限界条件:up=cp+r‘p>bestp。
r‘p 剩余物品装满背包的价值
6.2 单源最短路径问题
问题描述
在下图所给的有向图G中,每一边都有一个非负边权。要求图G的从源顶点s到目标顶点t之间的最短路径。
下图是用优先队列式分支限界法解有向图G的单源最短路径问题产生的解空间树。其中,每一个结点旁边的数字表示该结点所对应的当前路长。
算法思想
解单源最短路径问题的优先队列式分支限界法用一极小堆来存储活结点表。其优先级是结点所对应的当前路长。
算法从图G的源顶点s和空优先队列开始。结点s被扩展后,它的儿子结点被依次插入堆中。此后,算法从堆中取出具有最小当前路长的结点作为当前扩展结点,并依次检查与当前扩展结点相邻的所有顶点。如果从当前扩展结点i到顶点j有边可达,且从源出发,途经顶点i再到顶点j的所相应的路径的长度小于当前最优路径长度,则将该顶点作为活结点插入到活结点优先队列中。这个结点的扩展过程一直继续到活结点优先队列为空时为止。
实例说明
![[XJTUSE 算法设计与分析] 第六章 分支限界法_第7张图片](http://img.e-com-net.com/image/info8/4deebb2e9f204d52902bf3f2d7470c2d.jpg)
算法设计
static float[][]a //图G的邻接矩阵
static float []dist //源到各顶点的距离
static int []p //源到各顶点的路径上的前驱顶点
HeapNode //最小堆元素
{
int i; //顶点编号
float length;//当前路长
……
}
while (true) {
//搜索问题的解空间
for (int j = 1; j <= n; j++)
if ((a[enode.i][j]<Float.MAX_VALUE)&&
(enode.length+a[enode.i][j]<dist[j])) {
//顶点i和j间有边,且此路径长小于原先从原点到j的路径长
// 顶点i到顶点j可达,且满足控制约束
dist[j]= enode.length+c[enode.i][j];
p [j]= enode.i;
// 加入活结点优先队列
HeapNode node=new HeapNode(j,dist[j]);
heap.put(node);
}
// 取下一扩展结点
if ( heap.isEmpty( ) ) break;
else enode=(HeapNode)heap.removeMin();
}
}
6.3 0-1背包问题[重点]
解答参考https://www.it610.com/article/1296236014334976000.htm
问题描述
-
给定n种物品和一个背包。物品i的重量是wi,其价值为vi,背包的容量为c。
-
应如何选择装入背包的物品,使得装入背包中物品的总价值最大?
-
在选择装入背包的物品时,对每种物品i只有2种选择,即装入背包或不装入背包。不能将物品i装入背包多次,也不能只装入部分的物品i。
算法的思想
- 首先,要对输入数据进行预处理,将各物品依其单位重量价值从大到小进行排列。
- 在实现时,由Bound计算当前结点处的上界。在解空间树的当前扩展结点处,仅当要进入右子树时才计算右子树的上界Bound,以判断是否将右子树剪。进入左子树时不需要计算上界,因为其上界与其父节点上界相同。
- 在优先队列分支限界法中,结点的优先级定义为:以结点的价值上界作为优先级(由bound函数计算出)
步骤
- 算法首先根据基于可行结点相应的子树最大价值上界优先级,从堆中选择一个节点(根节点)作为当前可扩展结点。
- 检查当前扩展结点的左儿子结点的可行性。
- 如果左儿子结点是可行结点,则将它加入到子集树和活结点优先队列中。
- 当前扩展结点的右儿子结点一定是可行结点,
仅当右儿子结点满足上界函数约束时,才将它加入子集树和活结点优先队列。 - 当扩展到叶节点时,算法结束,叶子节点对应的解即为问题的最优值。
样例
假设有4个物品,其重量分别为(4, 7, 5, 3),价值分别为(40, 42, 25, 12),背包容量W=10。将给定物品按单位重量价值从大到小排序,结果如下:
| 物品 | 重量(w) | 价值(v) | 价值/重量(v/w) |
|---|---|---|---|
| 1 | 4 | 40 | 10 |
| 2 | 7 | 42 | 6 |
| 3 | 5 | 25 | 5 |
| 4 | 3 | 12 | 4 |
上界计算
先装入物品1,剩余的背包容量为6,只能装入物品2的6/7(即42*(6/7)=36)。 即上界为40+6*6=76
已第一个up为例:40+6*(10-4)=76
打x的部分因为up值已经小于等于bestp了,所以没必要继续递归了。
核心代码
- Typew c: 背包容量
- C: 背包容量
- Typew *w: 物品重量数组
- Typew *p: 物品价值数组
- Typew cw:当前重量
- Typew cp:当前价值
- Typep bestcp:当前最优价值
上界函数
template<class Typew, class Typep>
Typep Knap<Typew, Typep>::Bound(int i)
{
// 计算上界
Typew cleft = c - cw; // 剩余容量
Typep b = cp;
// 以剩余物品单位重量价值递减序装入物品
while (i <= n && w[i] <= cleft) {
cleft -= w[i];
b += p[i];
i++;
}
// 装满背包
if (i <= n) b += p[i]/w[i] * cleft;
return b;
}
结点定义
static class Bbnode{
BBnode parent; //父结点
boolean leftChild; //左儿子结点标志
…}
static class HeapNode implements Comparable{
BBnode liveNode; //活结点
double upperProfit; //结点的价值上界
double profit; //结点所相应的价值
double weight; //结点所相应的重量
int level; //活结点在子集树中所处的层序号
0-1背包问题优先队列分支限界搜索算法
![[XJTUSE 算法设计与分析] 第六章 分支限界法_第10张图片](http://img.e-com-net.com/image/info8/1ea109669a3248419292ff800271d8ba.jpg)
6.4 作业分配问题【重点】
详情参考https://blog.csdn.net/qq_40801709/article/details/90439784
1、问题描述
n 个操作员以 n 种不同时间完成 n 种不同作业。要求分配每位操作员完成一项工作,使完成 n 项工作的总时间最少操作员编号为 0,1,…n-1,作业也编号为 0,1,…n-1, 矩阵 c 描述每位操作员完成每个作业时所需的时间,元素 ci,j 表示第 i 位操作员完成第 j 号作业所需的时间 向量 x 描述分配给操作员的作业编号,分量 xi 表示分配给第 i 位操作员的作业编号。
2、思想方法
1)从根结点开始,每遇到一个扩展结点,就对它的所有儿子结点计算其下界,把它们登记在结点表中。
2)从表中选取下界最小的结点,重复上述过程。
3)当搜索到一个叶子结点时,如果该结点的下界是结点表中最小的,那么,该结点就是问题的最优解。
4)否则,对下界最小的结点继续进行扩展
3、下界的确认
搜索深度为 0 时,把第 0 号作业分配给第 i 位操作员所需时间至少为第 i 位操作员完成第 0 号作业所需时间,加上其余 n-1个作业分别由其余 n-1 位操作员单独完成时所需最短时间之和,有:![[XJTUSE 算法设计与分析] 第六章 分支限界法_第11张图片](http://img.e-com-net.com/image/info8/1e0a54454de442c88160b0ce76aca13f.png)
例:4个操作员完成4个作业所需的时间表如下:
![[XJTUSE 算法设计与分析] 第六章 分支限界法_第12张图片](http://img.e-com-net.com/image/info8/7dd0608c7d0e40d5a528a9633d7a7e68.png)
把第 0 号作业分配给第 0 位操作员时,所需时间至少不小于 3 + 7 + 6 + 3 = 19 ,把0号作业1 位操作员时,所需 时间至少不会小于9+7+4+3…
搜索深度为 k 时,前面第0,1,…,k-1号作业已分别分配 给编号为i0,i1,…,ik-1的操作员。 S={0,1,…,n-1}表示所有操作员的编号集合;
mk-1={i0,i1,…ik-1}表示作业已分配的操作员编号集合。当把第k号作业分配给编号为ik的操作员时, i k ∈ S − m k − 1 i_k\in S-m_{k-1} ik∈S−mk−1, 所需时间至少为:
则上式为把第k号作业分配给编号为ik的操作员时的下界
4、算法实现步骤
5、实现代码
#include![[XJTUSE 算法设计与分析] 第六章 分支限界法_第1张图片](http://img.e-com-net.com/image/info8/87c30d3c2cb0420ab3d37987da7cf189.jpg)
![[XJTUSE 算法设计与分析] 第六章 分支限界法_第2张图片](http://img.e-com-net.com/image/info8/12cff72d575f4abf92356cb914be6df3.jpg)
![[XJTUSE 算法设计与分析] 第六章 分支限界法_第3张图片](http://img.e-com-net.com/image/info8/a8442c6035d04a0d94d7077b22a2559e.jpg)
![[XJTUSE 算法设计与分析] 第六章 分支限界法_第4张图片](http://img.e-com-net.com/image/info8/5541ccd897d14414b22de384839773f7.jpg)
![[XJTUSE 算法设计与分析] 第六章 分支限界法_第5张图片](http://img.e-com-net.com/image/info8/9681f447da4349849aef6d8f1e46c150.jpg)
![[XJTUSE 算法设计与分析] 第六章 分支限界法_第6张图片](http://img.e-com-net.com/image/info8/b490d137d9864b4cb9b147bdef36c65f.jpg)
![[XJTUSE 算法设计与分析] 第六章 分支限界法_第8张图片](http://img.e-com-net.com/image/info8/8aff25d7c3a04f4a97d8821d97bb0847.jpg)
![[XJTUSE 算法设计与分析] 第六章 分支限界法_第9张图片](http://img.e-com-net.com/image/info8/5752b17dd08c4025a37be4570741695a.jpg)
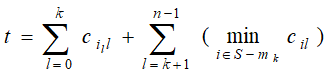
![[XJTUSE 算法设计与分析] 第六章 分支限界法_第13张图片](http://img.e-com-net.com/image/info8/c88800e7812b4ac6a65c72bef6bdf1c4.jpg)
![[XJTUSE 算法设计与分析] 第六章 分支限界法_第14张图片](http://img.e-com-net.com/image/info8/2c6581531dad4443aebb7a4d7d20a4df.jpg)