二叉排序(查找)树(Java实现)
二叉排序树:BST(Binary Sort(Search)Tree),又称为二叉查找树。其定义为:二叉排序树或者是一棵空树,或者是具有如下性质的二叉树。
① 若它的左子树非空,则左子树上所有节点的值均小于根节点的值,
② 若它的右子树非空,则右子树上的所有节点的值均大于(或大于等于)根节点的值。
③ 它的左右子树也分别为二叉排序树。
简单来说,对于二叉排序树的任何一个非叶子节点,要求左子节点的值比当前节点的值小,右子节点的值比当前节点的值大。若有相同的值,可将该节点放在左子节点或右子节点。
二叉排序树的创建
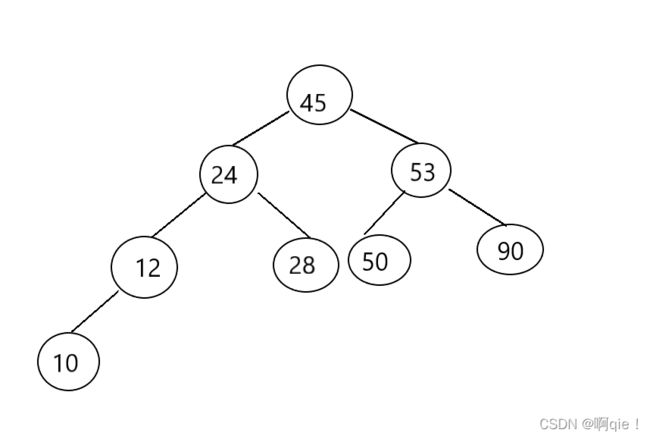
给定一个数组,用该数组创建对应的二叉排序树。比如数组为arr{45,24,53,12,28,10,50,90},则对应的二叉排序树为:
二叉排序树的删除
删除叶子节点:
1、需要先找到要删除的节点targetNode
2、找到targetNode的父节点parent
3、若targetNode是parent的左子节点,则parent.left = null;右子节点同理。
删除只有一颗子树的节点:
1、需要先找到要删除的节点targetNode
2、找到targetNode的父节点parent
3、确定targetNode的子节点是左子节点还是右子节点
4、targetNode是parent的左子节点还是右子节点
5、如果targetNode有左子节点
5.1、如果targetNode是parent的左子节点 parent.left = targetNode.left;
5.2、如果targetNode是parent的右子节点 parent.right = targetNode.left;
6、如果targetNode有右子节点
6.1、如果targetNode是parent的左子节点 parent.left = targetNode.right;
6.2、如果targetNode是parent的右子节点 parent.right = targetNode.right;
删除有两棵子树的节点:
1、需要先找到要删除的节点targetNode
2、从targetNode的右子树找到最小的节点(或者从targetNode的左子树找到最大的节点)
3、用一个临时变量,将最小(大)节点的值保存该变量中
4、删除该最小节点
5、targetNode.value = temp
二叉排序树的特性
根据二叉排序树的定义(左子树小于根节点,右子树大于根节点),根据二叉树中序遍历的定义(先中序遍历左子树,访问根节点,再中序遍历右子树),可以得出二叉排序树的一个重要性质:即中序遍历一个二叉排序树可以得到一个递增有序序列。
代码实现二叉排序树的创建、查找、删除
Node类:
package com.Tree.BST;
public class Node {
int value;
Node left;
Node right;
public Node() {
}
public Node(int value) {
this.value = value;
}
//查找要删除的结点
/**
*
* @param value 要删除结点的值
* @return 要是找到则返回该结点,否则返回null
*/
public Node search(int value) {
if(value == this.value) {
//找到直接返回
return this;
} else if(value < this.value) {
//如果查找的结点的值小于当前结点,向左子树递归查询
if(this.left == null) {
//如果左子节点为空则返回null
return null;
}
return this.left.search(value);
} else {
if(this.right == null) {
return null;
}
return this.right.search(value);
}
}
//查找要删除结点的父节点
/**
*
* @param value 要删除结点的值
* @return 要删除节点的父节点,如果没找到则返回null
*/
public Node searchParent(int value) {
//如果当前结点就是要查找结点的父节点,就返回
if((this.left != null && this.left.value == value) ||
(this.right != null && this.right.value == value)) {
return this;
} else if(value < this.value && this.left != null) {
//如果要查找的结点的值小于当前节点的值且当前结点的左子节点不为空
return this.left.searchParent(value); //向左子树递归查找
} else if(value > this.value && this.right != null) {
return this.right.searchParent(value);
} else {
return null; //没有找到父节点
}
}
//添加节点[递归的方式添加结点,要满足二叉排序树的规则]
public void add(Node node) {
if(node == null) {
return;
}
//判断传入结点的值和当前子树的根节点的值的关系
if(node.value < this.value) {
//如果当前结点的左子节点为null,则将node添加到当前结点的左子节点上
if(this.left == null) {
this.left = node;
} else {
//递归向左子树添加
this.left.add(node);
}
} else {
//传入结点的值大于等于当前子树的根节点的值
if(this.right == null) {
this.right = node;
} else {
//递归向右子树添加
this.right.add(node);
}
}
}
//中序遍历该BST树
public void infixOrder() {
if(this.left != null) {
this.left.infixOrder();
}
System.out.println(this);
if(this.right != null) {
this.right.infixOrder();
}
}
//前序遍历该树
public void preOrder() {
System.out.println(this);
if(this.left != null) {
this.left.preOrder();
}
if(this.right != null) {
this.right.preOrder();
}
}
/**
* 查找给定节点是否在该二叉树排序上
* @param value 要查找的节点的值
* @return 若找到返回true,没找到返回false
*/
public boolean contains(int value) {
if(this.value == value) {
return true;
} else if(value < this.value) {
if(this.left ==null) {
return false;
} else {
return this.left.contains(value);
}
} else {
if(this.right == null) {
return false;
} else {
return this.right.contains(value);
}
}
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
}
BinarySortTree类:
package com.Tree.BST;
public class BinarySortTree {
Node root;
public Node getRoot() {
return root;
}
//查找给定节点是否在该二叉树排序上
public boolean contains(int value) {
if(root == null) {
return false;
} else {
return root.contains(value);
}
}
//查找要删除的结点
public Node search(int value) {
if(root == null) {
return null;
} else {
return root.search(value);
}
}
//查找要删除结点的父节点
public Node searchParent(int value) {
if(root == null) {
return null;
} else {
return root.searchParent(value);
}
}
//删除节点
public void delNode(int value) {
if(root == null) {
return;
} else {
//找到要删除的节点
Node targetNode = search(value);
//如果没有找到要删除的节点就返回
if(targetNode == null) {
return;
}
//如果这个二叉排序树只有一个节点
if(root.left == null && root.right == null) {
root = null;
return;
}
//去找要删除节点的父节点
Node parent = searchParent(value);
//判断删除的是叶子节点
if(targetNode.left == null && targetNode.right == null) {
//判断删除的节点是父节点的左子节点还是右子节点
if(parent.left != null && parent.left.value == value) {
//是左子节点
parent.left = null;
} else if(parent.right != null && parent.right.value == value) {
parent.right = null;
}
} else if(targetNode.left != null && targetNode.right != null) {
//删除有两颗子树的节点
//从targetNode的右子树找到最小的节点,用临时变量保存该最小节点的值并删除,最后再吧临时变量的值赋给该节点的值
int minValue = delRightMin(targetNode.right);
targetNode.value = minValue;
//或者从targetNode的左子树找到最大的节点
//int maxValue = delLeftMax(targetNode.left);
//targetNode.value = maxValue;
} else {
//删除只有一颗子树的节点
if(targetNode.left != null) {
//若删除的节点有左子节点
//这里需要判断下父亲节点是否为空,如果不判断会出现空指针异常。因为如果二叉排序树只有根节点和它的一个左子节点,
// 刚好要删除这个根节点,由于它没有父亲节点,所以返回的是null
if(parent != null) {
if(parent.left.value == value) {
//targetNode是parent的左子节点
parent.left = targetNode.left;
} else {
///targetNode是parent的右子节点
parent.right = targetNode.left;
}
} else {
root = targetNode.left;
}
} else {
//删除的节点有右子节点
if(parent != null) {
//同理也需要判段父亲节点是否为空
if(parent.left.value == value) {
//targetNode是parent的左子节点
parent.left = targetNode.right;
} else {
parent.right = targetNode.right;
}
} else {
root = targetNode.right;
}
}
}
}
}
/**
* 返回以node为根节点的二叉排序树的最小节点的值
* 删除以node为根节点的二叉排序树的最小节点
* @param node 传入的节点(当作二叉排序树的根节点)
* @return 返回以node为根节点的二叉排序树的最小节点的值
*/
public int delRightMin(Node node) {
Node target = node;
while(target.left != null) {
target = target.left;
}
//退出while循环时,target就指向了最小节点;
delNode(target.value);
return target.value;
}
public int delLeftMax (Node node) {
Node target = node;
while(target.right != null) {
target = target.right;
}
//退出while循环时,target就指向了最大节点
delNode(target.value);
return target.value;
}
//中序遍历BST
public void infixOrder() {
if(root != null) {
root.infixOrder();
} else {
System.out.println("空树,无法遍历");
}
}
//前序遍历该树
public void preOrder() {
if(root != null) {
root.preOrder();
} else {
System.out.println("null");
}
}
//添加节点
public void add(Node node) {
if(root == null) {
root = node; //如果root为空,令其直接指向node
} else {
root.add(node);
}
}
}
测试类:
package com.Tree.BST;
public class BSTDemo {
public static void main(String[] args) {
int[] arr = {
45,24,53,12,28,10,50,90};
BinarySortTree bst = new BinarySortTree();
for (int i = 0; i < arr.length; i++) {
bst.add(new Node(arr[i]));
}
// bst.delNode(45);
bst.infixOrder();
System.out.println(bst.contains(9));
}
}