数据结构之---C语言实现最短路径之Dijkstra（迪杰斯特拉）算法

此处共同拥有两段代码：

一、

这段代码比較全面，当中參考了github上的相关源代码。

能够说功能强大。

//Dijkstra（迪杰斯特拉算法）
#include 
#include 
#include 


#define MAX         100                 // 矩阵最大容量
#define INF         65535        		// 最大值65535
#define isLetter(a) ((((a)>='a')&&((a)<='z')) || (((a)>='A')&&((a)<='Z')))
#define LENGTH(a)   (sizeof(a)/sizeof(a[0]))

// 图的邻接矩阵存储
typedef struct _graph
{
    char vexs[MAX];       // 顶点集合
    int vexnum;           // 顶点数
    int edgnum;           // 边数
    int matrix[MAX][MAX]; // 邻接矩阵
}Graph, *PGraph;

// 边的结构体
typedef struct _EdgeData
{
    char start; // 边的起点
    char end;   // 边的终点
    int weight; // 边的权重
}EData;

/*
 * 返回ch在matrix矩阵中的位置
 */
static int get_position(Graph G, char ch)
{
    int i;
    for(i=0; i (v * (v-1))))
    {
        printf("输入有误！！

!\n"); return NULL; } if ((pG=(Graph*)malloc(sizeof(Graph))) == NULL ) return NULL; memset(pG, 0, sizeof(Graph)); //初始化 // 初始化"顶点数"和"边数" pG->vexnum = v; pG->edgnum = e; // 初始化"顶点" for (i = 0; i < pG->vexnum; i++) { printf("vertex(%d): ", i); pG->vexs[i] = read_char(); } // 1. 初始化"边"的权值 for (i = 0; i < pG->vexnum; i++) { for (j = 0; j < pG->vexnum; j++) { if (i==j) pG->matrix[i][j] = 0; else pG->matrix[i][j] = INF; } } // 2. 初始化"边"的权值: 依据用户的输入进行初始化 for (i = 0; i < pG->edgnum; i++) { // 读取边的起始顶点，结束顶点，权值 printf("edge(%d):", i); c1 = read_char(); c2 = read_char(); scanf("%d", &weight); p1 = get_position(*pG, c1); p2 = get_position(*pG, c2); if (p1==-1 || p2==-1) { printf("输入有误!!!\n"); free(pG); return NULL; } pG->matrix[p1][p2] = weight; pG->matrix[p2][p1] = weight; } return pG; } /* * 创建图(用已提供的矩阵) */ Graph* create_example_graph() { char vexs[] = {'A', 'B', 'C', 'D', 'E', 'F', 'G'}; int matrix[][9] = { /*A*//*B*//*C*//*D*//*E*//*F*//*G*/ /*A*/ { 0, 12, INF, INF, INF, 16, 14}, /*B*/ { 12, 0, 10, INF, INF, 7, INF}, /*C*/ { INF, 10, 0, 3, 5, 6, INF}, /*D*/ { INF, INF, 3, 0, 4, INF, INF}, /*E*/ { INF, INF, 5, 4, 0, 2, 8}, /*F*/ { 16, 7, 6, INF, 2, 0, 9}, /*G*/ { 14, INF, INF, INF, 8, 9, 0}}; int vlen = LENGTH(vexs); int i, j; Graph* pG; // 输入"顶点数"和"边数" if ((pG=(Graph*)malloc(sizeof(Graph))) == NULL ) return NULL; memset(pG, 0, sizeof(Graph)); // 初始化"顶点数" pG->vexnum = vlen; // 初始化"顶点" for (i = 0; i < pG->vexnum; i++) pG->vexs[i] = vexs[i]; // 初始化"边" for (i = 0; i < pG->vexnum; i++) for (j = 0; j < pG->vexnum; j++) pG->matrix[i][j] = matrix[i][j]; // 统计边的数目 for (i = 0; i < pG->vexnum; i++) for (j = 0; j < pG->vexnum; j++) if (i!=j && pG->matrix[i][j]!=INF) pG->edgnum++; pG->edgnum /= 2; return pG; } /* * 返回顶点v的第一个邻接顶点的索引。失败则返回-1 */ static int first_vertex(Graph G, int v) { int i; if (v<0 || v>(G.vexnum-1)) return -1; for (i = 0; i < G.vexnum; i++) if (G.matrix[v][i]!=0 && G.matrix[v][i]!=INF) return i; return -1; } /* * 返回顶点v相对于w的下一个邻接顶点的索引，失败则返回-1 */ static int next_vertix(Graph G, int v, int w) { int i; if (v<0 || v>(G.vexnum-1) || w<0 || w>(G.vexnum-1)) return -1; for (i = w + 1; i < G.vexnum; i++) if (G.matrix[v][i]!=0 && G.matrix[v][i]!=INF) return i; return -1; } /* * 深度优先搜索遍历图的递归实现 */ static void DFS(Graph G, int i, int *visited) { int w; visited[i] = 1; printf("%c ", G.vexs[i]); // 遍历该顶点的全部邻接顶点。若是没有訪问过。那么继续往下走 for (w = first_vertex(G, i); w >= 0; w = next_vertix(G, i, w)) { if (!visited[w]) DFS(G, w, visited); } } /* * 深度优先搜索遍历图 */ void DFSTraverse(Graph G) { int i; int visited[MAX]; // 顶点訪问标记 // 初始化全部顶点都没有被訪问 for (i = 0; i < G.vexnum; i++) visited[i] = 0; printf("DFS: "); for (i = 0; i < G.vexnum; i++) { //printf("\n== LOOP(%d)\n", i); if (!visited[i]) DFS(G, i, visited); } printf("\n"); } /* * 广度优先搜索（相似于树的层次遍历） */ void BFS(Graph G) { int head = 0; int rear = 0; int queue[MAX]; // 辅组队列 int visited[MAX]; // 顶点訪问标记 int i, j, k; for (i = 0; i < G.vexnum; i++) visited[i] = 0; printf("BFS: "); for (i = 0; i < G.vexnum; i++) { if (!visited[i]) { visited[i] = 1; printf("%c ", G.vexs[i]); queue[rear++] = i; // 入队列 } while (head != rear) { j = queue[head++]; // 出队列 for (k = first_vertex(G, j); k >= 0; k = next_vertix(G, j, k)) //k是为訪问的邻接顶点 { if (!visited[k]) { visited[k] = 1; printf("%c ", G.vexs[k]); queue[rear++] = k; } } } } printf("\n"); } /* * 打印矩阵队列图 */ void print_graph(Graph G) { int i,j; printf("Martix Graph:\n"); for (i = 0; i < G.vexnum; i++) { for (j = 0; j < G.vexnum; j++) printf("%10d ", G.matrix[i][j]); printf("\n"); } } /* * prim最小生成树 * * 參数说明： * G -- 邻接矩阵图 * start -- 从图中的第start个元素開始。生成最小树 */ void prim(Graph G, int start) { int min,i,j,k,m,n,sum; int index=0; // prim最小树的索引，即prims数组的索引 char prims[MAX]; // prim最小树的结果数组 int weights[MAX]; // 顶点间边的权值 // prim最小生成树中第一个数是"图中第start个顶点"，由于是从start開始的。 prims[index++] = G.vexs[start]; // 初始化"顶点的权值数组"， // 将每一个顶点的权值初始化为"第start个顶点"到"该顶点"的权值。

for (i = 0; i < G.vexnum; i++ ) weights[i] = G.matrix[start][i]; // 将第start个顶点的权值初始化为0。 // 能够理解为"第start个顶点到它自身的距离为0"。

weights[start] = 0; for (i = 0; i < G.vexnum; i++) { // 由于从start開始的，因此不须要再对第start个顶点进行处理。 if(start == i) continue; j = 0; k = 0; min = INF; // 在未被增加到最小生成树的顶点中。找出权值最小的顶点。

while (j < G.vexnum) { // 若weights[j]=0。意味着"第j个节点已经被排序过"(或者说已经增加了最小生成树中)。 if (weights[j] != 0 && weights[j] < min) { min = weights[j]; k = j; } j++; } // 经过上面的处理后，在未被增加到最小生成树的顶点中，权值最小的顶点是第k个顶点。 // 将第k个顶点增加到最小生成树的结果数组中 prims[index++] = G.vexs[k]; // 将"第k个顶点的权值"标记为0。意味着第k个顶点已经排序过了(或者说已经增加了最小树结果中)。 weights[k] = 0; // 当第k个顶点被增加到最小生成树的结果数组中之后，更新其他顶点的权值。 for (j = 0 ; j < G.vexnum; j++) { // 当第j个节点没有被处理，而且须要更新时才被更新。

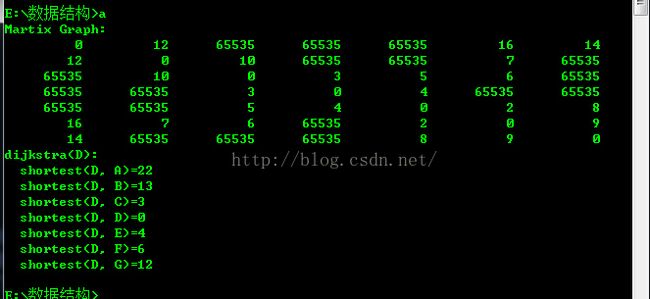
if (weights[j] != 0 && G.matrix[k][j] < weights[j]) weights[j] = G.matrix[k][j]; } } // 计算最小生成树的权值 sum = 0; for (i = 1; i < index; i++) { min = INF; // 获取prims[i]在G中的位置 n = get_position(G, prims[i]); // 在vexs[0...i]中，找出到j的权值最小的顶点。 for (j = 0; j < i; j++) { m = get_position(G, prims[j]); if (G.matrix[m][n] edges[j].weight) { // 交换"第i条边"和"第j条边" EData tmp = edges[i]; edges[i] = edges[j]; edges[j] = tmp; } } } } /* * 获取i的终点 */ int get_end(int vends[], int i) { while (vends[i] != 0) i = vends[i]; return i; } /* * 克鲁斯卡尔（Kruskal)最小生成树 */ void kruskal(Graph G) { int i,m,n,p1,p2; int length; int index = 0; // rets数组的索引 int vends[MAX]={0}; // 用于保存"已有最小生成树"中每一个顶点在该最小树中的终点。 EData rets[MAX]; // 结果数组，保存kruskal最小生成树的边 EData *edges; // 图相应的全部边 // 获取"图中全部的边" edges = get_edges(G); // 将边依照"权"的大小进行排序(从小到大) sorted_edges(edges, G.edgnum); for (i=0; i

* * 參数说明： * G -- 图 * vs -- 起始顶点(start vertex)。即计算"顶点vs"到其他顶点的最短路径。 * prev -- 前驱顶点数组。即。prev[i]的值是"顶点vs"到"顶点i"的最短路径所经历的全部顶点中，位于"顶点i"之前的那个顶点。 * dist -- 长度数组。即。dist[i]是"顶点vs"到"顶点i"的最短路径的长度。 */ void dijkstra(Graph G, int vs, int prev[], int dist[]) { int i,j,k; int min; int tmp; int flag[MAX]; // flag[i]=1表示"顶点vs"到"顶点i"的最短路径已成功获取。 // 初始化 for (i = 0; i < G.vexnum; i++) { flag[i] = 0; // 顶点i的最短路径还没获取到。 prev[i] = 0; // 顶点i的前驱顶点为0。

dist[i] = G.matrix[vs][i];// 顶点i的最短路径为"顶点vs"到"顶点i"的权。

} // 对"顶点vs"自身进行初始化 flag[vs] = 1; dist[vs] = 0; // 遍历G.vexnum-1次；每次找出一个顶点的最短路径。 for (i = 1; i < G.vexnum; i++) { // 寻找当前最小的路径； // 即。在未获取最短路径的顶点中，找到离vs近期的顶点(k)。

min = INF; for (j = 0; j < G.vexnum; j++) { if (flag[j]==0 && dist[j]

INF : (min + G.matrix[k][j])); // 防止溢出 if (flag[j] == 0 && (tmp < dist[j]) ) { dist[j] = tmp; prev[j] = k; } } } // 打印dijkstra最短路径的结果 printf("dijkstra(%c): \n", G.vexs[vs]); for (i = 0; i < G.vexnum; i++) printf(" shortest(%c, %c)=%d\n", G.vexs[vs], G.vexs[i], dist[i]); } int main() { int prev[MAX] = {0}; int dist[MAX] = {0}; Graph* pG; // 自己定义"图"(输入矩阵队列) //pG = create_graph(); // 採用已有的"图" pG = create_example_graph(); print_graph(*pG); // 打印图 //DFSTraverse(*pG); // 深度优先遍历 //BFS(*pG); // 广度优先遍历 //prim(*pG, 0); // prim算法生成最小生成树 //kruskal(*pG); // kruskal算法生成最小生成树 // dijkstra算法获取"第4个顶点"到其他各个顶点的最短距离 dijkstra(*pG, 3, prev, dist); return 0; }

结果图：

二、

这段比較简单，相对来说好理解些。

#include 
#include 
#define MAX 1000000
int arcs[10][10];//邻接矩阵
int D[10];//保存最短路径长度
int p[10][10];//路径
int final[10];//若final[i] = 1则说明 顶点vi已在集合S中
int n = 0;//顶点个数
int v0 = 0;//源点
int v,w;
void ShortestPath_DIJ()
{
	 int i = 0, min = 0;
     for (v = 0; v < n; v++) //循环 初始化
     {
          final[v] = 0; D[v] = arcs[v0][v];
          for (w = 0; w < n; w++) p[v][w] = 0;//设空路径
          if (D[v] < MAX) {p[v][v0] = 1; p[v][v] = 1;}
     }
     D[v0] = 0; final[v0]=0; //初始化 v0顶点属于集合S
     //開始主循环 每次求得v0到某个顶点v的最短路径 并加v到集合S中
     for (i = 1; i < n; i++)
     {
          min = MAX;
          for (w = 0; w < n; w++)
          {
               //我觉得的核心过程--选点
               if (!final[w]) //假设w顶点在V-S中
               {
                    //这个过程终于选出的点 应该是选出当前V-S中与S有关联边
                    //且权值最小的顶点 书上描写叙述为 当前离V0近期的点
                    if (D[w] < min) {v = w; min = D[w];}
               }
          }
          final[v] = 1; //选出该点后增加到合集S中
          for (w = 0; w < n; w++)//更新当前最短路径和距离
          {
               /*在此循环中 v为当前刚选入集合S中的点
               则以点V为中间点 考察 d0v+dvw 是否小于 D[w] 假设小于 则更新
               比方加进点 3 则若要考察 D[5] 是否要更新 就 推断 d(v0-v3) + d(v3-v5) 的和是否小于D[5]
               */
               if (!final[w] && (min+arcs[v][w]

结果：