区间算法题用线段树可以秒解？

区间算法题用线段树可以秒解？

背景

给一个两个数组，其中一个数组是 A [1,2,3,4]，另外一个数组是 B [5,6,7,8]。让你求两个数组合并后的大数组的：

• 最大值
• 最小值
• 总和

这题是不是很简单？我们直接可以很轻松地在 $O(m+n)$ 的时间解决，其中 m 和 n 分别为数组 A 和 B 的大小。

那如果我可以修改 A 和 B 的某些值，并且我要求很多次最大值，最小值和总和呢？

朴素的思路是原地修改数组，然后 $O(m+n)$ 的时间重新计算。显然这并没有利用之前计算好的结果，效率是不高的。 那有没有效率更高的做法？

有！线段树就可以解决。

线段树是什么？

线段树本质上就是一棵树。更准确地说，它是一颗二叉树，而且它是一颗平衡二叉树。关于为什么是平衡二叉树，我们后面会讲，这里大家先有这样一个认识。

虽然是一棵二叉树，但是线段树我们通常使用数组来模拟树结构，而不是传统的定义 TreeNode 。

一方面是因为实现起来容易，另外一方面是因为线段树其实是一颗完全二叉树，因此使用数组直接模拟会很高效。这里的原因我已经在之前写的堆专题中的二叉堆实现的时候中讲过了，大家可以在我的公众号《力扣加加》回复堆获取。

解决什么问题

正如它的名字，线段树和线段（区间）有关。线段树的每一个树节点其实都存储了一个区间（段）的信息。然后这些区间的信息如果满足一定的性质就可以用线段树来提高性能。

那：

1. 究竟是什么样的性质？
2. 如何提高的性能呢？

究竟是什么样的性质？

比如前面我们提到的最大值，最小值以及求和就满足这个一定性质。即我可以根据若干个（这里是两个）子集推导出子集的并集的某一指标。

以上面的例子来说，我们可以将数组 A 和 数组 B 看成两个集合。那么：集合 A 的最大值和集合 B 的最大值已知，我们可以直接通过 max(Amax, Bmax) 求得集合 A 与集合 B 的并集的最大值。其中 Amax 和 Bmax 分别为集合 A 和集合 B 的最大值。最小值和总和也是一样的，不再赘述。因此如果统计信息满足这种性质，我们就可以可以使用线段树。但是要不要使用，还是要看用了线段树后，是否能提高性能。

如何提高的性能呢？

关于提高性能，我先卖一个关子，等后面讲完实现的时候，我们再聊。

实现

以文章开头的求和为例。

我们可以将区间 A 和 区间 B 分别作为一个树的左右节点，并将 A 的区间和与 B 的区间和分别存储到左右子节点中。

接下来，将 A 的区间分为左右两部分，同理 B 也分为左右两部分。不断执行此过程直到无法继续分。

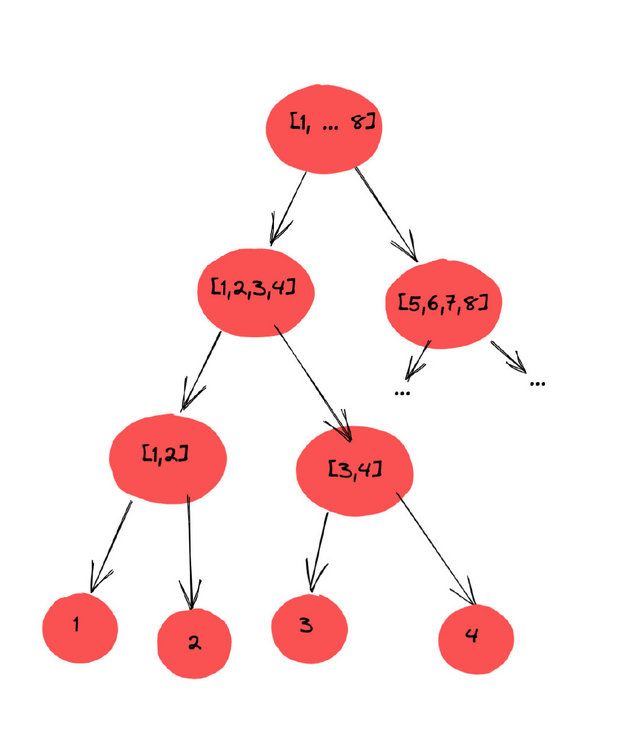
总结一下就是将区间不断一分为二，并将区间信息分别存储到左右节点。如果是求和，那么区间信息就是区间的和。这个时候的线段树大概是这样的：

蓝色字体表示的区间和。

注意，这棵树的所有叶子节点一共有 n 个（n 为原数组长度），并且每一个都对应到原数组某一个值。

体现到代码上也很容易。 直接使用后续遍历即可解决。这是因为，我们需要知道左右节点的统计信息，才能计算出当前节点的统计信息。

不熟悉后序遍历的可以看下我之前的树专题，公众号力扣加加回复树即可获取

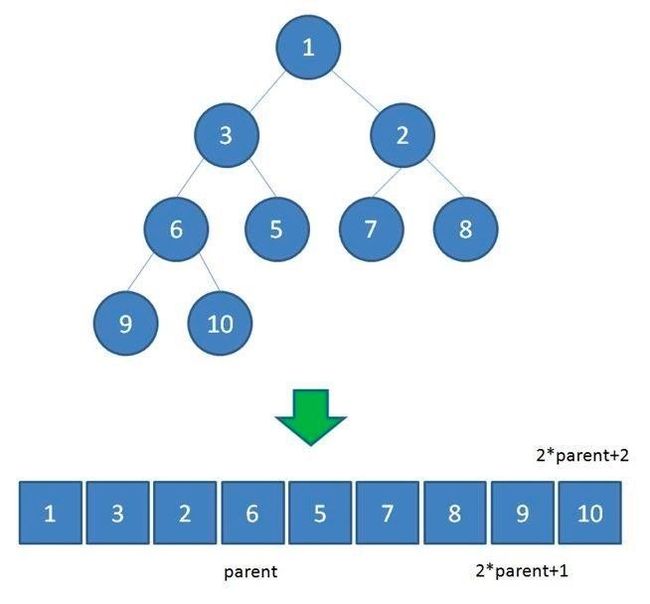
和二叉堆的表示方式一样，我们可以用数组表示树，用 2 * i + 1 和 2 * 1 + 2 来表示左右节点的索引，其中 i 为当前节点对应在 tree 上的索引。

tree 是用来构建线段树的数组，和二叉堆类似。只不过 tree[i] 目前存的是区间信息罢了。

上面我描述建树的时候有明显的递归性，因此我们可以递归的建树。具体来说，可以定义一个 build(tree_index, l, r) 方法 来建树。其中 l 和 r 就是对应区间的左右端点，这样 l 和 r 就可以唯一确定一个区间。 tree_index 其实是用来标记当前的区间信息应该被更新到 tree 数组的哪个位置。

我们在 tree 上存储区间信息，那么最终就可以用 tree[tree_index] = .... 来更新区间信息啦。

核心代码：

def build(self, tree_index:int, l:int, r:int):
    '''
    递归创建线段树
    tree_index : 线段树节点在数组中位置
    l, r : 该节点表示的区间的左，右边界
    '''
    if l == r:
        self.tree[tree_index] = self.data[l]
        return
    mid = (l+r) // 2 # 区间中点，对应左孩子区间结束，右孩子区间开头
    left, right = 2 * tree_index + 1, 2 * tree_index + 2 # tree_index 的左右子树索引
    self.build(left, l, mid)
    self.build(right, mid+1, r)
    # 典型的后序遍历
    # 区间和使用加法即可，如果不是区间和要改下面这行代码
    self.tree[tree_index] = self.tree[left] + self.tree[right]

上面代码的数组 self.tree[i] 其实就是用来存类似上图中蓝色字体的区间和。每一个区间都在 tree 上存有它一个位置，存它的区间和。

复杂度分析

• 时间复杂度：由递推关系式 T(n) = 2*T(n/2) + 1，因此时间复杂度为 $O(n)$

不知道怎么得出的 $O(n)$? 可以看下我的《算法通关之路》的第一章内容。 https://leetcode-solution.cn/...

• 空间复杂度：tree 的大小和 n 同阶，因此空间复杂度为 $O(n)$

终于把树建好了，但是知道现在一点都没有高效起来。我们要做的是高效处理频繁更新情况下的区间查询。

那基于这种线段树的方法，如果更新和查询区间信息如何做呢？

区间查询

先回答简单的问题区间查询原理是什么。

如果查询一个区间的信息。这里也是使用后序遍历就 ok 了。比如我要找一个区间 [l,r] 的区间和。

那么如果当前左节点：

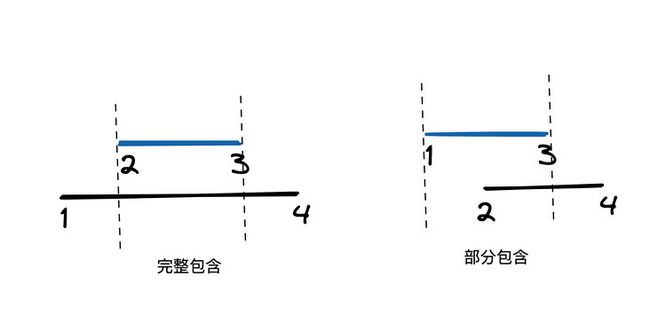
• 完整地落在 [l,r] 内。比如 [2,3] 完整地落在 [1,4] 内。 我们直接将 tree 中左节点对于的区间和取出来备用，不妨极为 lsum。
• 部分落在 [l,r] 内。比如 [1,3] 部分落在 [2,4]。这个时候我们继续递归，直到完整地落在区间内（上面的那种情况），这个时候我们直接将 tree 中左节点对于的区间和取出来备用
• 将前面所有取出来备用的值加起来就是答案

右节点的处理也是一样的，不再赘述。

复杂度分析

• 时间复杂度：查询不需要在每个时刻都处理两个叶子节点，实际上处理的次数大致和树的高度一致。而树是平衡的，因此复杂度为 $O(logn)$

或者由递推关系式 T(n) = T(n/2) + 1，因此时间复杂度为 $O(logn)$

不知道怎么得出的 $O(logn)$? 可以看下我的《算法通关之路》的第一章内容。 https://leetcode-solution.cn/...

大家可以结合后面的代码理解这个复杂度。

区间修改

那么如果我修改了 A[1] 为 1 呢？

如果不修改 tree，那么显然查询的区间只要包含了 A[1] 就一定是错的，比如查询区间 [1,3] 的和 就会得到错误的答案。因此我们要在修改了 A[1] 的时候同时去修改 tree。

问题在于我们要修改哪些 tree 的值，修改为多少呢？

首先回答第一个问题，修改哪些 tree 的值呢？

我们知道，线段树的叶子节点都是原数组上的值，也是说，线段树的 n 个叶子节点对应的就是原数组。因此我们首先要找到我们修改的位置对应的那个叶子节点，将其值修改掉。

这就完了么？

没有完。实际上，我们修改的叶子节点的所有父节点以及祖父节点（如果有的话）都需要改。也就是说我们需要从这个叶子节点不断冒泡到根节点，并修改沿途的区间信息

这个过程和浏览器的事件模型是类似的

接下来回答最后一个问题，具体修改为多少？

对于求和，我们需要首先将叶子节点改为修改后的值，另外所有叶子节点到根节点路径上的点的区间和都加上 delta，其中 delta 就是改变前后的差值。

求最大最小值如何更新？大家自己思考一下。

修改哪些节点，修改为多少的问题都解决了，那么代码实现就容易了。

复杂度分析

• 时间复杂度：修改不需要在每个时刻都处理两个叶子节点，实际上处理的次数大致和树的高度一致。而树是平衡的，因此复杂度为 $O(logn)$

或者由递推关系式 T(n) = T(n/2) + 1，因此时间复杂度为 $O(logn)$

不知道怎么得出的 $O(logn)$? 可以看下我的《算法通关之路》的第一章内容。 https://leetcode-solution.cn/...

大家可以结合后面的代码理解这个复杂度。

代码

线段树代码已经放在刷题插件上了，公众号《力扣加加》回复插件即可获取。

class SegmentTree:
    def __init__(self, data:List[int]):
        '''
        data: 传入的数组
        '''
        self.data = data
        self.n = len(data)
        #  申请 4 倍 data 长度的空间来存线段树节点
        self.tree = [None] * (4 * self.n) # 索引 i 的左孩子索引为 2i+1，右孩子为 2i+2
        if self.n:
            self.build(0, 0, self.n-1)
    # 本质就是一个自底向上的更新过程
    # 因此可以使用后序遍历，即在函数返回的时候更新父节点。
    def update(self, tree_index, l, r, index):
        '''
        tree_index: 某个根节点索引
        l, r : 此根节点代表区间的左右边界
        index : 更新的值的索引
        '''
        if l == r==index :
            self.tree[tree_index] = self.data[index]
            return
        mid = (l+r)//2
        left, right = 2 * tree_index + 1, 2 * tree_index + 2
        if index > mid:
            # 要更新的区间在右子树
            self.update(right, mid+1, r, index)
        else:
            # 要更新的区间在左子树 index<=mid
            self.update(left, l, mid, index)
        # 查询区间一部分在左子树一部分在右子树
        # 区间和使用加法即可，如果不是区间和要改下面这行代码
        self.tree[tree_index] = self.tree[left] + self.tree[right]

    def updateSum(self,index:int,value:int):
        self.data[index] = value
        self.update(0, 0, self.n-1, index)
    def query(self, tree_index:int, l:int, r:int, ql:int, qr:int) -> int:
        '''
        递归查询区间 [ql,..,qr] 的值
        tree_index : 某个根节点的索引
        l, r : 该节点表示的区间的左右边界
        ql, qr: 待查询区间的左右边界
        '''
        if l == ql and r == qr:
            return self.tree[tree_index]

        # 区间中点，对应左孩子区间结束，右孩子区间开头
        mid = (l+r) // 2
        left, right = tree_index * 2 + 1, tree_index * 2 + 2
        if qr <= mid:
            # 查询区间全在左子树
            return self.query(left, l, mid, ql, qr)
        elif ql > mid:
            # 查询区间全在右子树
            return self.query(right, mid+1, r, ql, qr)

        # 查询区间一部分在左子树一部分在右子树
        # 区间和使用加法即可，如果不是区间和要改下面这行代码
        return self.query(left, l, mid, ql, mid) + self.query(right, mid+1, r, mid+1, qr)

    def querySum(self, ql:int, qr:int) -> int:
        '''
        返回区间 [ql,..,qr] 的和
        '''
        return self.query(0, 0, self.n-1, ql, qr)

    def build(self, tree_index:int, l:int, r:int):
        '''
        递归创建线段树
        tree_index : 线段树节点在数组中位置
        l, r : 该节点表示的区间的左，右边界
        '''
        if l == r:
            self.tree[tree_index] = self.data[l]
            return
        mid = (l+r) // 2 # 区间中点，对应左孩子区间结束，右孩子区间开头
        left, right = 2 * tree_index + 1, 2 * tree_index + 2 # tree_index 的左右子树索引
        self.build(left, l, mid)
        self.build(right, mid+1, r)
        # 区间和使用加法即可，如果不是区间和要改下面这行代码
        self.tree[tree_index] = self.tree[left] + self.tree[right]

相关专题

• 堆

大家可以看下我之前写的堆的专题的二叉堆实现。然后对比学习，顺便还学了堆，岂不美哉？

• 树状数组

树状数组和线段树类似，难度比线段树稍微高一点点。有机会给大家写一篇树状数组的文章。

• immutablejs

前端的小伙伴应该知道 immutable 吧？ 而 immutablejs 就是非常有名的实现 immutable 的工具库。西法之前写过一篇 immutable 原理解析文章，感兴趣的可以看下 https://lucifer.ren/blog/2020...

回答前面的问题

为啥是平衡二叉树？

前面的时间复杂度其实也是基于树是平衡二叉树这一前提。那么线段树一定是平衡二叉树么？是的。这是因为线段树是完全二叉树，而完全二叉树是平衡的。

当然还有另外一个前提，那就是树的总的节点数和原数组长度同阶，也就是 n 的量级。关于为啥是同阶的，也容易计算，只需要根据递归公式即可得出。

为啥线段树能提高性能？

只要你理解了我实现部分的时间复杂度，那么就不难明白这个问题。因为修改和查询的时间复杂度都是 $logn$，而不使用线段树的暴力做法查询的复杂度高达 $O(n)$。相应的代价就是建树的 $O(n)$ 的空间，因此线段树也是一种典型的空间换时间算法。

最后点一下题。区间算法题是否可以用线段树秒解？这其实文章中已经回答过了，其取决于是否满足两点：

1. 是否可以根据若干个（这里是两个）子集推导出子集的并集的某一指标。
2. 是否能提高性能（相比于朴素的暴力解法）。通常面临频繁修改的场景都可以考虑使用线段树优化修改后的查询时间消耗。