语音信号是连续的一维模拟信号,而计算机只能够处理离散的数字信号。故要想利用计算机处理语音信号,首先要对连续的语音信号进行离散化处理。
根据奈奎斯特采样定理,当采样频率大于信号最大频率的两倍时,采样后的信号能够恢复成原信号。
具体过程是首先从语音数据中经过特征提取得到声学特征,然后经过模型训练统计得到一个声学模型(声学模型对应于语音到音素的概率计算),作为识别的模板,并结合语言模型(音素到文字的概率计算)经过解码处理得到一个识别结果。
1.特征提取
第一步我们要对音频数据进行特征提取。常见的特征提取都是基于人类的发声机理和听觉感知,从发声机理到听觉感知认识声音的本质。
常用的一些声学特征如下:
(1) 线性预测系数( LPC ),线性预测分析是模拟人类的发声原理,通过分析声道短管级联的模型得到的。假设系统的传递函数跟全极点的数字滤波器是相似的,通常用 12 一 16 个极点就可以描述语音信号的特征。所以对于 n 时刻的语音信号, 我们可以用之前时刻的信号的线性组合近似的模拟。然后计算语音信号的采样值和线性预测的采样值,并让这两者之间达到均方的误差( MSE )最小,就可以得到 LPC。
(2) 感知线性预测( PLP ),PLP 是一种基于听觉模型的特征参数。该参数是一种等效于 LPC 的特征,也是全极点模型预测多项式的一组系数。不同之处是 PLP 是基于入耳昕觉,通过计算应用到频谱分析中,将输入语音信号经过入耳听觉模型处理,替代 LPC 所用的时域信号,这样的优点是有利于抗噪语音特征的提取。
(3)梅尔频率倒谱系数( MFCC ),MFCC 也是基于入耳听觉特性,梅尔频率倒谱频带划分是在 Mel 刻度上等距划的,Mel 频率的尺度值与实际频率的对数分布关系更符合人耳的听觉特性,所以可以使得语音信号有着更好的表示。
(5)基于滤波器组的特征 Fbank(Filter bank),Fbank 特征提取方法就是相当 于 MFCC 去掉最后一步的离散余弦变换,跟 MFCC 特征,Fbank 特征保留了更多的原始语音数据。
(6)语谱图( Spectrogram ),语谱图就是语音频谱图,一般是通过处理接收的时域信号得到频谱图,因此只要有足够时间长度的时域信号就可。语谱图的特点是观察语音不同频段的信号强度,可以看出随时间的变化情况。
本文就是通过将语谱图作为特征输入,利用 CNN 进行图像处理进行训练。语谱图可以理解为在一段时间内的频谱图叠加而成,因此提取语谱图的主要步骤分为:分帧、加窗、快速傅立叶变换( FFT )。
1.1读取音频
import scipy.io.wavfile as wav
import matplotlib.pyplot as plt
import os
# 随意搞个音频做实验
filepath = 'test.wav'
fs, wavsignal = wav.read(filepath)
print(type(wavsignal))
print(wavsignal.shape)
plt.plot(wavsignal)
plt.show()
1.2 分帧、加窗
从宏观上看,它必须足够短来保证帧内信号是平稳的。前面说过,口型的变化是导致信号不平稳的原因,所以在一帧的期间内口型不能有明显变化,即一帧的长度应当小于一个音素的长度。正常语速下,音素的持续时间大约是 50~200 毫秒,所以帧长一般取为小于 50 毫秒。从微观上来看,它又必须包括足够多的振动周期,因为傅里叶变换是要分析频率的,只有重复足够多次才能分析频率语音的基频,男声在 100 赫兹左右,女声在 200 赫兹左右,换算成周期就是 10 毫秒和 5 毫秒。既然一帧要包含多个周期,所以一般取至少 20 毫秒。
加窗的目的是让一帧信号的幅度在两端渐变到 0。渐变对傅里叶变换有好处,可以提高变换结果(即频谱)的分辨率。加窗的代价是一帧信号两端的部分被削弱了,没有像中央的部分那样得到重视。弥补的办法是,帧不要背靠背地截取,而是相互重叠一部分。相邻两帧的起始位置的时间差叫做帧移,常见的取法是取为帧长的一半,或者固定取为 10 毫秒。
为了处理语音信号,我们要对语音信号进行加窗,也就是一次仅处理窗中的数据。因为实际的语音信号是很长的,我们不能也不必对非常长的数据进行一次性处理。明智的解决办法就是每次取一段数据,进行分析,然后再取下一段数据,再进行分析。
在对非周期信号做傅里叶变换时,要将非周期信号作周期延拓(加窗),使非周期信号变为周期信号,再进行傅里叶变化。但非周期信号在做周期延拓时,可能会在原信号中引入新的频率分量,即发生频谱泄露。
由于直接对信号(加矩形窗)截断会产生频谱泄露,为了改善频谱泄露的情况,加非矩形窗,一般都是加汉明窗,因为汉明窗的幅频特性是旁瓣衰减较大,主瓣峰值与第一个旁瓣峰值衰减可达43db。因为加上汉明窗,只有中间的数据体现出来了,两边的数据信息丢失了,所以等会移窗的时候,只会移1/3或1/2窗,这样被前一帧或二帧丢失的数据又重新得到了体现。
公式为:
import numpy as np
x=np.linspace(0, 400 - 1, 400, dtype = np.int64)#返回区间内的均匀数字
w = 0.54 - 0.46 * np.cos(2 * np.pi * (x) / (400 - 1))
plt.plot(w)
plt.show()
# 帧长: 25ms 帧移: 10ms 采样点(帧)= fs / 1000 * 帧长
time_window = 25
window_length = fs // 1000 * time_window
# 分帧
p_begin = 0
p_end = p_begin + window_length
frame = wavsignal[p_begin:p_end]
plt.figure(figsize=(15, 5))
ax4 = plt.subplot(121)
ax4.set_title('the original picture of one frame')
ax4.plot(frame)
# 加窗
frame = frame * w
ax5 = plt.subplot(122)
ax5.set_title('after hanmming')
ax5.plot(frame)
plt.show()
1.3 快速傅立叶变换 (FFT)
傅里叶变换要求输入信号是平稳的,从微观上来看,在比较短的时间内,嘴巴动得是没有那么快的,语音信号就可以看成平稳的,就可以截取出来做傅里叶变换了。
语音信号在时域上比较难看出其特性,所以通常转换为频域上的能量分布,所以我们对每帧经过窗函数处理的信号做快速傅立叶变换将时域图转换成各帧的频谱,然后我们可以对每个窗口的频谱叠加得到语谱图。
代码为:
from scipy.fftpack import fft
# 进行快速傅里叶变换
frame_fft = np.abs(fft(frame))[:200]
plt.plot(frame_fft)
plt.show()
# 取对数,求 db
frame_log = np.log(frame_fft)
plt.plot(frame_log)
plt.show()
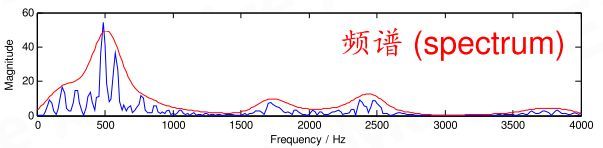
横轴是频率,纵轴是幅度。频谱上就能看出这帧语音在 480 和 580 赫兹附近的能量比较强。语音的频谱,常常呈现出「精细结构」和「包络」两种模式。「精细结构」就是蓝线上的一个个小峰,它们在横轴上的间距就是基频,它体现了语音的音高——峰越稀疏,基频越高,音高也越高。「包络」则是连接这些小峰峰顶的平滑曲线(红线),它代表了口型,即发的是哪个音。包络上的峰叫共振峰,图中能看出四个,分别在 500、1700、2450、3800 赫兹附近。有经验的人,根据共振峰的位置,就能看出发的是什么音。
# 该函数提取音频文件的时频图
import numpy as np
import scipy.io.wavfile as wav
from scipy.fftpack import fft
# 获取信号的时频图
def compute_fbank(file):
x=np.linspace(0, 400-1, 400, dtype=np.int64)
w = 0.54-0.46*np.cos(2*np.pi*(x)/(400-1)) # 汉明窗
fs, wavsignal = wav.read(file)
# wav波形 加时间窗以及时移10ms
time_window = 25 # 单位ms
window_length = fs/1000*time_window # 计算窗长度的公式,目前全部为400固定值
wav_arr = np.array(wavsignal)
wav_length = len(wavsignal)
range0_end = int(len(wavsignal)/fs*1000-time_window) // 10 # 计算循环终止的位置,也就是最终生成的窗数
data_input = np.zeros((range0_end, 200), dtype=np.float) # 用于存放最终的频率特征数据
data_line = np.zeros((1, 400), dtype=np.float) # 窗口内的数据
for i in range(0, range0_end):
p_start = i*16000/100 # 步长10ms所以
p_end = p_start+400 # 窗口长25ms
data_line = wav_arr[p_start:p_end]
data_line = data_line*w # 加窗
data_line = np.abs(fft(data_line))
data_input[i]=data_line[0:200] # 设置为400除以2的值(即200)是取一半数据,因为是对称的
data_input = np.log(data_input+1)
return data_input
import matplotlib.pyplot as plt
filepath = 'test.wav'
a = compute_fbank(filepath)
# print(a.shape)
plt.imshow(a.T, origin = 'lower')
plt.show()
a.shape
2 CTC (Connectionist Temporal Classification)
谈及语音识别,如果这里有一个剪辑音频的数据集和对应的转录,而我们不知道怎么把转录中的字符和音频中的音素对齐,这会大大增加了训练语音识别器的难度。如果不对数据进行调整处理,那就意味着不能用一些简单方法进行训练。对此,我们可以选择的第一个方法是制定一项规则,如“一个字符对应十个音素输入”,但人们的语速千差万别,这种做法很容易出现纰漏。为了保证模型的可靠性,第二种方法,即手动对齐每个字符在音频中的位置,训练的模型性能效果更佳,因为我们能知道每个输入时间步长的真实信息。但它的缺点也很明显——即便是大小合适的数据集,这样的做法依然非常耗时。事实上,制定规则准确率不佳、手动调试用时过长不仅仅出现在语音识别领域,其它工作,如手写识别、在视频中添加动作标记,同样会面对这些问题。
这种场景下,正是 CTC 用武之地。CTC 是一种让网络自动学会对齐的好方法,十分适合语音识别和书写识别。为了描述地更形象一些,我们可以把输入序列(音频)映射为,其相应的输出序列(转录)即为 。这之后,将字符与音素对齐的操作就相当于在 X 和 Y 之间建立一个准确的映射,详细内容可见CTC 经典文章。
损失函数部分代码:
def ctc_lambda(args):
labels, y_pred, input_length, label_length = args
y_pred = y_pred[:, :, :]
return K.ctc_batch_cost(labels, y_pred, input_length, label_length)
解码部分代码:
#num_result 为模型预测结果,num2word 对应拼音列表。
def decode_ctc(num_result, num2word):
result = num_result[:, :, :]
in_len = np.zeros((1), dtype = np.int32)
in_len[0] = result.shape[1];
r = K.ctc_decode(result, in_len, greedy = True, beam_width=10, top_paths=1)
r1 = K.get_value(r[0][0])
r1 = r1[0]
text = []
for i in r1:
text.append(num2word[i])
return r1, text
3. 声学模型
模型主要利用 CNN 来处理图像并通过最大值池化来提取主要特征加入定义好的 CTC 损失函数来进行训练。当有了输入和标签的话,模型构造就可以自己进行设定,如果准确率得以提升,那么都是可取的。有兴趣也可以加入 LSTM 等网络结构,关于 CNN 和池化操作网上资料很多,这里就不再赘述了。有兴趣的读者可以参考往期的卷积神经网络 AlexNet 。
代码:
class Amodel():
"""docstring for Amodel."""
def __init__(self, vocab_size):
super(Amodel, self).__init__()
self.vocab_size = vocab_size
self._model_init()
self._ctc_init()
self.opt_init()
def _model_init(self):
self.inputs = Input(name='the_inputs', shape=(None, 200, 1))
self.h1 = cnn_cell(32, self.inputs)
self.h2 = cnn_cell(64, self.h1)
self.h3 = cnn_cell(128, self.h2)
self.h4 = cnn_cell(128, self.h3, pool=False)
# 200 / 8 * 128 = 3200
self.h6 = Reshape((-1, 3200))(self.h4)
self.h7 = dense(256)(self.h6)
self.outputs = dense(self.vocab_size, activation='softmax')(self.h7)
self.model = Model(inputs=self.inputs, outputs=self.outputs)
def _ctc_init(self):
self.labels = Input(name='the_labels', shape=[None], dtype='float32')
self.input_length = Input(name='input_length', shape=[1], dtype='int64')
self.label_length = Input(name='label_length', shape=[1], dtype='int64')
self.loss_out = Lambda(ctc_lambda, output_shape=(1,), name='ctc')\
([self.labels, self.outputs, self.input_length, self.label_length])
self.ctc_model = Model(inputs=[self.labels, self.inputs,
self.input_length, self.label_length], outputs=self.loss_out)
def opt_init(self):
opt = Adam(lr = 0.0008, beta_1 = 0.9, beta_2 = 0.999, decay = 0.01, epsilon = 10e-8)
self.ctc_model.compile(loss={'ctc': lambda y_true, output: output}, optimizer=opt)
4. 语言模型
4.1 介绍统计语言模型
统计语言模型是自然语言处理的基础,它是一种具有一定上下文相关特性的数学模型,本质上也是概率图模型的一种,并且广泛应用于机器翻译、语音识别、拼音输入、图像文字识别、拼写纠错、查找错别字和搜索引擎等。在很多任务中,计算机需要知道一个文字序列是否能构成一个大家理解、无错别字且有意义的句子,比如这几句话:
许多人可能不太清楚到底机器学习是什么,而它事实上已经成为我们日常生活中不可或缺的重要组成部分。
不太清楚许多人可能机器学习是什么到底,而它成为已经日常我们生活中组成部分不可或缺的重要。
不清太多人机可楚器学许能习是么到什底,而已常我它成经日为们组生中成活部不重可的或缺分要。
第一个句子符合语法规范,词义清楚,第二个句子词义尚且还清楚,第三个连词义都模模糊糊了。这正是从基于规则角度去理解的,在上个世纪 70 年代以前,科学家们也是这样想的。而之后,贾里尼克使用了一个简单的统计模型就解决了这个问题。从统计角度来看,第一个句子的概率很大,而第二个其次,第三个最小。按照这种模型,第一个句子出现的概率是第二个的 10 的 20 次方倍,更不用说第三个句子了,所以第一个句子最符合常理。
4.2 模型建立
假设 S 为生成的句子,有一连串的词 构成,则句子 S 出现的概率为:
由于计算机内存空间和算力的限制,我们明显需要更加合理的运算方法。一般来说,仅考虑与前一个词有关,就可以有着相当不错的准确率,在实际使用中,通常考虑与前两个词有关就足够了,极少情况下才考虑与前三个有关,因此我们可以选择采取下列这个公式:
而我们可以通过爬取资料统计词频来进行计算概率。
4.3 拼音到文本的实现
拼音转汉字的算法是动态规划,跟寻找最短路径的算法基本相同。我们可以将汉语输入看成一个通信问题,每一个拼音可以对应多个汉字,而每个汉字一次只读一个音,把每一个拼音对应的字从左到有连起来,就成为了一张有向图。5. 模型测试
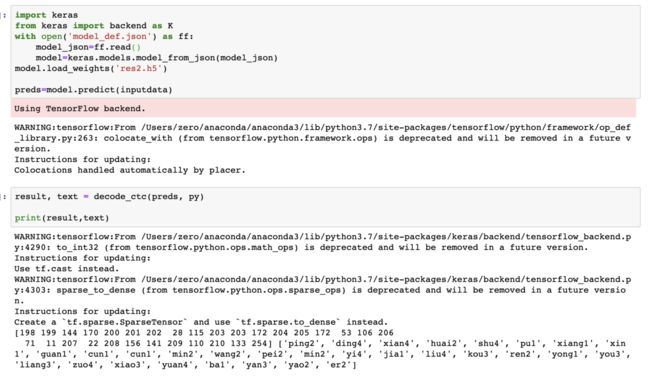
声学模型测试:
语言模型测试:
由于模型简单和数据集过少,模型效果并不是很好。
项目源码地址:https://momodel.cn/explore/5d5b589e1afd9472fe093a9e?type=app