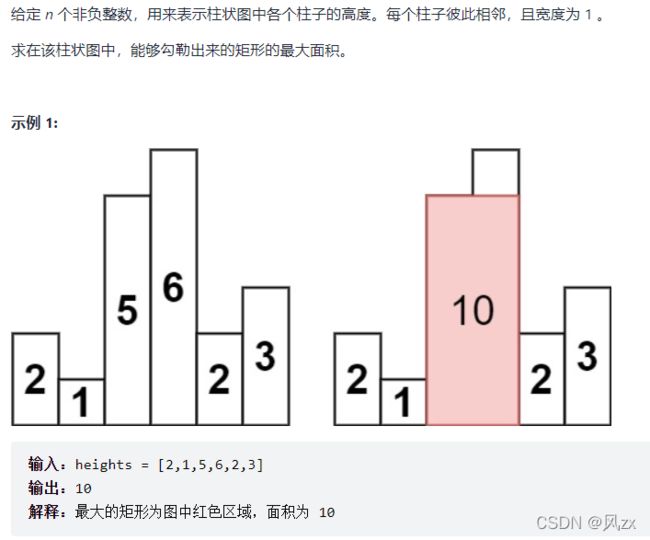
LeetCode 84:柱状图中最大的矩形(困难)
解答
这两道单调栈的题目需要好好反思一下,为什么思路大体正确但是都没有做出来
代码一
思路一模仿接雨水中双指针的方法,
- 接雨水中是要找到 val 左右两侧中最高的柱子,取min得到水平面高度
- 本题中是要找到val 往左往右拓展, 尽可能往左/往右 大于等于 val的柱子索引,这个就是计算宽度,高度就是val
好像都是根据val, 找到宽的制约因素。这个思路自己想出来了,但是没有写代码,因为最坏情况复杂度为O(n^2),
但是下面的代码复杂度应该略高于O(n),while部分的复杂度不好分析,使用了并查集记录,空间换时间,heights[t] >= heights[i]时,heigits[t]高于heights[i],heights[t]左边第一个小于该柱子的柱子minLeftIndex[t],有可能高于heights[i],有可能低于heights[i],
- 如果低于heights[i],则minLeftIndex[t]到heights[i]的区间内没有低于heights[t]的柱子了,全是高于heights[t] (heights[t] >= heights[i])的柱子,所以minLeftIndex[i] = t;
- 如果高于heights[i],那么重复上述过程

class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
vector<int> minLeftIndex(heights.size());
vector<int> minRightIndex(heights.size());
int size = heights.size();
// 记录每个柱子 左边第一个小于该柱子的下标
minLeftIndex[0] = -1; // 注意这里初始化,防止下面while死循环
for (int i = 1; i < size; i++) {
int t = i - 1;
// 这里不是用if,而是不断向左寻找的过程
while (t >= 0 && heights[t] >= heights[i]) t = minLeftIndex[t];
minLeftIndex[i] = t;
}
// 记录每个柱子 右边第一个小于该柱子的下标
minRightIndex[size - 1] = size; // 注意这里初始化,防止下面while死循环
for (int i = size - 2; i >= 0; i--) {
int t = i + 1;
// 这里不是用if,而是不断向右寻找的过程
while (t < size && heights[t] >= heights[i]) t = minRightIndex[t];
minRightIndex[i] = t;
}
// 求和
int result = 0;
for (int i = 0; i < size; i++) {
int sum = heights[i] * (minRightIndex[i] - minLeftIndex[i] - 1);
result = max(sum, result);
}
return result;
}
};
代码二
自己一开始思考的是找到 尽可能往左/往右 大于等于 val的柱子索引,因为想尽可能往左往右拓展。
但是考虑单调递减栈(从栈顶到栈底递减),比如1,3,5,每个元素的下一个(从栈顶到栈底)都是左边小于该元素的第一个(在入栈时,进行必要的出栈后,栈顶元素的右边第一个比自己大的数是当前元素,同样,当前元素的左边的第一个比自己小的数是栈顶,然后当前元素入栈)。实际上就是在一维数组中对每一个数找到第一个比自己小的元素。 用大于等于 val的柱子考虑就不太合适了。
考虑一个单调递减栈,比如1,3,2,当1,3入栈后,2要入栈时,此时对于3而言,左边第一个小于3的元素是1,右边第一个小于3的元素是2,3找到了左右边界。
在比如1,2,3,当1,2入栈后,3入栈时,此时对于2而言,左边第一个小于2的元素是1,右边第一个小于2的元素还未知(因为3可以直接入栈)。
也就是当前可以计算的是出栈元素柱子的最大矩形
核心是单调栈的用途:
左边/右边 找到第一个比自己 大/小 的元素
上面写的比较乱,拿例子举例就清晰一点了
从左往右,从栈顶到栈底递减:1,3,5,4 ,2, 找到左边/右边 第一个小于自己的元素,注意now=4时,5要出栈,左边是栈内的3,右边是now=4,注意4左边第一个比自己小的是3,出栈元素5右边第一个比自己小的是4
从左往右,从栈顶到栈底递增:5,3,1,2 ,4, 找到左边/右边 第一个大于自己的元素
// my solution
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
stack<int> st;
int now=0, left=0, right=0, mid=0, ans=0;
for(int i=0; i<heights.size(); i++){
now = heights[i];
if(st.empty()) st.push(i);
else if(now > heights[st.top()]) st.push(i);
else if(now == heights[st.top()]) {// 因为找到是左边第一个小于val的元素索引
st.pop();
st.push(i);
}
else{ // now < heights[st.top()], 比如:1,3,2
while(!st.empty() && now < heights[st.top()]){
mid = st.top();
st.pop();
if(st.empty()) { // heights[mid]左边没有
ans = max(ans, (i-0)*heights[mid]);
break;
}
right = i;
left = st.top();
ans = max(ans, (right-left-1)*heights[mid]);
}
st.push(i);
}
}
right = heights.size();
while(!st.empty()){
mid = st.top();
st.pop();
if(st.empty()){
ans = max(ans, (int)(heights[mid] * heights.size() ));
break;
}
left = st.top();
ans = max(ans, (right-left-1)*heights[mid]);
// right = left;
}
return ans;
}
};
代码三
与代码一类似,同样是往左往右找第一个小于该元素的柱子,使用上述描述的单调递减栈(从栈顶到栈底递减)
从左往右使用递减栈找到每个元素左边第一个小于该元素的值,从右往左使用递减栈找到每个元素右边第一个小于该元素的值
每个元素至多入栈一次,出栈一次,所以复杂度为O(n)
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
int n = heights.size();
vector<int> left(n), right(n);
stack<int> mono_stack;
for (int i = 0; i < n; ++i) {
while (!mono_stack.empty() && heights[mono_stack.top()] >= heights[i]) {
mono_stack.pop();
}
left[i] = (mono_stack.empty() ? -1 : mono_stack.top());
mono_stack.push(i);
}
mono_stack = stack<int>();
for (int i = n - 1; i >= 0; --i) {
while (!mono_stack.empty() && heights[mono_stack.top()] >= heights[i]) {
mono_stack.pop();
}
right[i] = (mono_stack.empty() ? n : mono_stack.top());
mono_stack.push(i);
}
int ans = 0;
for (int i = 0; i < n; ++i) {
ans = max(ans, (right[i] - left[i] - 1) * heights[i]);
}
return ans;
}
};
小结
核心问题是找到左边右边第一个小于该元素的索引(注意不是大于等于),熟悉单调栈后应该比较自然的想到代码三的思路,从左往右、从右往左遍历两遍
代码二的思路是,从左往右遍历一遍,就可以同时确定 每个元素左边右边第一个小于该元素的索引,(eg:从左往右,从栈顶到栈底递减:1,3,5,4 ,2),