WebGL绘制基本图形--线

前言

地图的渲染其实可以分解为线、面、纹理、文字的渲染。为了了解地图渲染的实现原理并实际练习WebGL，进行了这个系列的练习，线是第一步。

本文不赘述WebGL的基本知识，只对运用到的知识点进行一下简单的回顾：

着色器

WebGL需要两种着色器：顶点着色器和片元着色器，以OpenGL ES着色器语言进行编写，本文中使用的着色器如下：

var VSHADER_SOURCE = 
  'attribute vec4 a_Position;\n' +  // 顶点坐标
  'uniform mat4 u_MvpMatrix;\n' +   // 模型视图投影矩阵
  'void main() {\n' +
  '  gl_Position = u_MvpMatrix * a_Position;\n' +
  '}\n';
var FSHADER_SOURCE = 
  'precision mediump float;\n' +
  'uniform vec4 u_Color;\n' +
  'void main() {\n' +
  '  gl_FragColor = u_Color;\n' +   // 颜色
  '}\n';

考虑到绘制一条线使用同一种颜色，与顶点无关，所以在片元着色器中定义了一个uniform变量u_Color。

三角形

WebGL绘制模型的基本单位是三角形，绘制一条有宽度的线并不能像Canvas2D那样设置strokeStyle之后调用stroke()即可，而是需要将整条线拆分成多个小三角形，这个过程称为三角剖分。

线段本身的三角剖分是很简单的，即矩形剖分为两个三角形。但是折线有拐角（lineJoin）和端头（lineCap），且需要支持不同的样式，这部分的剖分会稍微复杂一点，后文会详细分析。

WebGL的drawArrays方法支持多种模式进行多个三角形的绘制，如下所示：

drawArrays模式

矢量

三角剖分的计算过程中使用到了矢量和矩阵的一些基本运算，涉及到了矢量的加减法、乘法、单位化、旋转等，这些读者应自行了解和掌握。本文封装了二维矢量的相关计算方法到Vector2类中。

/**
 * Constructor of Vector2
 * If opt_src is specified, new vector is initialized by opt_src.
 * @param opt_src source vector(option)
 */
function Vector2(opt_src) {
  var v = new Float32Array(2);
  if (opt_src && typeof opt_src === 'object') {
    v[0] = opt_src[0]; v[1] = opt_src[1];
  } 
  this.elements = v;
}

/**
 * Vector2.prototype.normalize 单位化
 * Vector2.prototype.scalarProduct 与标量相乘
 * Vector2.prototype.dotProduct 与矢量点乘
 * Vector2.prototype.add 与矢量相加
 * Vector2.prototype.minus 与矢量相减
 * Vector2.prototype.rotate 旋转角度
 * Vector2.prototype.copy 复制
 * Vector2.prototype.getVertical 获取单位法向量
 * /

绘制目标

线这里专指折线，使用线段将一组离散的坐标点依次连接而形成。由于地图是呈现在z=0平面上，本文也只探讨在同一平面上延伸的线（扁平的），所以线的坐标点不用关心z坐标，使用二维矢量（x, y）即可。后文以coords表示线的坐标数组。

除了coords，线的样式也是其重要的属性。如下例所示，线可设置宽度、颜色，同时可设置边线的宽度和颜色；端头以canvas为标准，可支持三种样式：butt-平头，square-方头，round-圆头；拐角以canvas为标准，支持三种样式：bevel-平角，miter-尖角，round-圆角。

defaultLineStyle = {
  strokeColor: new WebglColor(0.5, 0.5, 1, 1), // 边线颜色
  strokeWidth: 5,  // 边线宽度
  fillColor: new WebglColor(0.9, 0.9, 1, 1),  // 线颜色
  fillWidth: 20,  // 线宽度
  lineCap: 'butt',  // 端头样式
  lineJoin: 'bevel'  // 拐角样式
}

[站外图片上传中...(image-c011bf-1545711490022)]

为了之后的一系列练习，本文封装了一个Shape类用于WebGL绘制基本图形，抽象出了一个构造的接口和通用的方法、属性如下：

构造函数：new Shape(opts)，参数说明如下

字段名	类型	说明
type	String	图形类型：`polyline`, `polygon`, `circle`
glCtx	WebGLRenderingContext	WebGL绘图上下文
camera	Matrix4	视图投影矩阵
coords	Array.	坐标
style	Object	样式（不同图形类型支持的样式字段不同）

方法

方法	返回值	说明
setCamera(camera: Matrix4)	None	设置视图投影矩阵
setCoords(coords: Array.)	None	设置坐标
setStyle(style: Object)	None	设置样式

另外还封装了WebglColor、Matrix4、Vector2，最终使用示例如下：

/**
 * 创建Camera矩阵
 * @param {Number} width 画布宽度
 * @param {Number} height 画布高度
 * @param {Number} pitch 视线俯仰角
 */
function createCamera(width, height, pitch) {
  var camera = new Matrix4();
  var fov = 60;
  var distance = height / 2 / Math.tan(fov / 2 / 180 * Math.PI);
  var near = 1;
  var far = 1.5 * distance;
  var aspect = width / height;
  camera.setPerspective(fov, aspect, near, far);
  camera.lookAt(0, 0, distance, 0, 0, 0, 0, 1, 0);

  camera.rotate(pitch, 1, 0, 0);
  return camera;
}

var canvas = document.getElementById('webgl');
var gl = canvas.getContext('webgl');
var camera = createCamera(canvas.clientWidth, canvas.clientHeight, -30);  // 构建视图投影矩阵

var polyline = new Shape({
  type: 'polyline',
  glCtx: gl,
  camera: camera,
  coords: [100,100,-100,100,-100,0,100,0,100,-100,-100,-100],
  style: {
    strokeColor: new WebglColor(0.5, 0.5, 1, 1),
    strokeWidth: 5,
    fillColor: new WebglColor(0.9, 0.9, 1, 1),
    fillWidth: 20
  }
});
// 构造完成或重置属性之后会自动绘制图形

具体实现

绘制流程

我们先了解一下绘制的整体流程，然后依次详解每个步骤。

function drawSolidLine(gl, camera, coords, style) {
  var mvpMatrix = camera;
  var color = style.color;
  
  // 三角剖分
  var triangulation = getLineTriangulation(coords, style);

  // 创建并初始化着色器，获取变量存储位置
  var locations = initUColorShader(gl);
  if (!locations) {
    return;
  }

  // 创建缓冲区并传入数据
  var vertices = triangulation.vertices;
  if (!initVertexBuffers(gl, vertices)) {
    return;
  }
  
  // 变量赋值
  gl.uniformMatrix4fv(locations.u_MvpMatrix, false, mvpMatrix.elements);
  gl.uniform4f(locations.u_Color, color.r, color.g, color.b, color.a);
  gl.vertexAttribPointer(locations.a_Position, 3, gl.FLOAT, false, 0, 0);
  gl.enableVertexAttribArray(location.a_Position);

  // 执行绘制任务
  var tasks = triangulation.tasks;
  tasks.forEach(function(task) {
    gl.drawArrays(gl[task.mode], task.start, task.cnt);
  });
}

如代码所示：

三角剖分：不同图形的剖分过程不同，最终返回剖分后的顶点数组、绘制任务。每个绘制任务指明了顶点索引范围及绘制模式。

triangulation = {
  vertices: [x0, y0, z, x1, y1, z, ...]
  tasks: [task0, task1, ...]
}

创建并初始化着色器，获取变量存储位置：
initUColorShader创建一个单一颜色的着色器，然后创建、使用程序，获取并返回着色器中每个变量的存储位置。

locations = {
  a_Position: ..,
  u_MvpMatrix: ..,
  u_Color: ..
}

创建缓冲区并传入数据：
进行缓冲区的创建、绑定等操作，将三角剖分后得到的顶点数组triangulation.vertices写入缓冲区
变量赋值：
为着色器中的变量赋值，向存储位置locations写入数据
执行绘制任务：
遍历triangulation.tasks，按指定的模式、索引范围进行绘制

下文详细讲解每个步骤的具体实现。

三角剖分

线的剖分可以分解为三个部分，一是线段，二是端头，三是拐角。

1. 准备工作

转换coords为二维点，并计算每个线段的单位法向量。因为需要在路径上进行垂直扩宽，且宽度与线段长度无关，所以法向量取单位长度即可。

// 将坐标转换为点、线段矢量、线段单位法向量
var path = [],
    segments = [],
    verticalVectors = [],
    pathLength = 0;
for (let index = 0; index < coords.length; index += 2) {
  let x = coords[index];
  let y = coords[index + 1];
  let pathPoint = new Point2([x, y]);
  path.push(pathPoint);

  if (pathLength) {
    // 相邻两点相减得到线段矢量
    let prePoint = path[pathLength - 1];
    let segment = pathPoint.minus(prePoint);
    segments.push(segment);
    verticalVectors.push(segment.getVertical());
  }

  pathLength++;
}

准备工作

2. 线段剖分

线段剖分比较简单，在路径点坐标上加扩宽的法向量即可，需注意连接两个线段的路径点需要根据两条线段的法向量，拓展出4个顶点。

path.forEach((pathPoint, index) => {
  // basePoints为扩宽后的顶点坐标
  var width = style.width / 2;
  var v0 = index == 0 ? null : verticalVectors[index-1].copy().scalarProduct(width);
  var v1 = index == pathLength - 1 ? null : verticalVectors[index].copy().scalarProduct(width);
  if (v0) {
    basePoints.push(pathPoint.add(v0));
    basePoints.push(pathPoint.minus(v0));
  }
  if (v1) {
    basePoints.push(pathPoint.add(v1));
    basePoints.push(pathPoint.minus(v1));
  }
});

basePoints

TRIANGLE_STRIP方式绘制

3. 端头剖分

端头只需要在首尾路径点上进行扩展。端头支持三种样式：butt不需要增加坐标点，square需要扩展出半个正方形，边长为线宽，round需要扩展出半个圆形，直径为线宽。
square端头剖分需要找到正方形的顶点，只需将线段法向量旋转90度，即可得到偏移向量offsetVector，示意图如下：

square端头

round端头剖分需要在圆形弧线上找到等距且密集的点，只需将线段法向量以小角度旋转n次直到2*PI，即可得到弧线上的顶点，最终将圆心与顶点以TRIANGLE_FAN的方式绘制即可实现圆形，示意图如下：

round端头

function getLineCapTrigl(pathPoint, verticalVector, style, isHead) {
  var subPoints = [];
  var mode = "TRIANGLE_STRIP";
  var width = style.width / 2;
  var v = verticalVector.copy().scalarProduct(width);
  switch (style.lineCap) {
    case 'butt':
      break;
    case 'square':
      var offsetVector = v.getVertical().scalarProduct(width);
      if (isHead) {
        subPoints.push(pathPoint.add(v).add(offsetVector));
        subPoints.push(pathPoint.minus(v).add(offsetVector));
      } else {
        subPoints.push(pathPoint.add(v).minus(offsetVector));
        subPoints.push(pathPoint.minus(v).minus(offsetVector));
      }
      subPoints.push(pathPoint.add(v));
      subPoints.push(pathPoint.minus(v));
      break;
    case 'round':
      subPoints.push(pathPoint);
      var rotateVector;
      for (let angle = 0; angle < 2.1 * Math.PI; angle += Math.PI/16) {
        rotateVector = v.rotate(angle);
        subPoints.push(pathPoint.add(rotateVector));
      }
      mode = "TRIANGLE_FAN";
      break;
    default:
      console.error('Invalid lineCap:' + style.lineCap);
  }
  return {
    points: subPoints,
    mode: mode
  };
}

4. 拐角剖分

拐角是在除去首尾两端的路经点上进行扩展。支持三种样式：bevel不需要增加坐标点（线段剖分后连接处自然形成了平角），miter需要填补线段延长线交汇出的尖角，round需要填补扇形，直径为线宽。
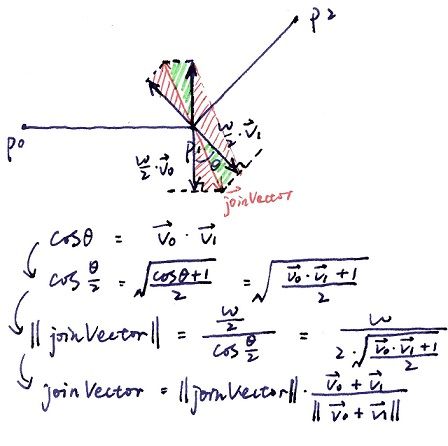
miter的剖分相对来说比较复杂一点，如下图所示，并非是一个菱形，而是两个以线段法向量为直角边的直角三角形拼接而成，计算公式如下：

miter拐角

function getLineJoinTrigl(pathPoint, v0, v1, style) {
  var subPoints = [];
  var mode = "TRIANGLE_STRIP";
  var width = style.width / 2;
  var v0_scale = v0.copy().scalarProduct(width);
  var v1_scale = v1.copy().scalarProduct(width);
  switch (style.lineJoin) {
    case 'miter':
      var length = width / Math.sqrt((v0.dotProduct(v1) + 1) / 2);
      var joinVector = v0.add(v1).normalize().scalarProduct(length);
      subPoints.push(pathPoint);
      subPoints.push(pathPoint.add(v0_scale));
      subPoints.push(pathPoint.add(joinVector));
      subPoints.push(pathPoint.add(v1_scale));
      subPoints.push(pathPoint.minus(v0_scale));
      subPoints.push(pathPoint.minus(joinVector));
      subPoints.push(pathPoint.minus(v1_scale));
      mode = "TRIANGLE_FAN";
      break;
    case 'bevel':
      break;
    case 'round':
      subPoints.push(pathPoint);
      var rotateVector;
      for (let angle = 0; angle < 2.1 * Math.PI; angle += Math.PI/16) {
        rotateVector = v0_scale.rotate(angle);
        subPoints.push(pathPoint.add(rotateVector));
      }
      mode = "TRIANGLE_FAN";
      break;
    default:
      console.error('Invalid lineJoin:' + style.lineJoin);
  }
  return {
    points: subPoints,
    mode: mode
  };
}

初始化着色器

initUColorShader负责建立和初始化着色器，主要分为三个步骤，一是通过UColorShader()获取单一颜色着色器代码；二是创建并使用程序；三是获取变量位置。

/**
 * 创建并初始化着色器
 * @param {WebGLRenderingContext} gl 
 */
function initUColorShader(gl) {
  // 获取着色器代码
  var shaders = UColorShader();
  // 创建并使用程序
  if (!initShaders(gl, shaders.vshader, shaders.fshader)) {
    console.error('Failed to intialize shaders.');
    return null;
  }
  // 获取变量位置
  return getLocations();
}

1. 着色器代码

如前文所述，UColorShader用以生成单一颜色着色器，代码如下：

/**
 * UColorShader: 单颜色着色器
 * 单一颜色u_Color，支持矩阵变换u_MvpMatrix, 顶点坐标a_Position
 */
function UColorShader() {
  var VSHADER_SOURCE = 
    'attribute vec4 a_Position;\n' +
    'uniform mat4 u_MvpMatrix;\n' +
    'void main() {\n' +
    '  gl_Position = u_MvpMatrix * a_Position;\n' +
    '}\n';
  var FSHADER_SOURCE = 
    'precision mediump float;\n' +
    'uniform vec4 u_Color;\n' +
    'void main() {\n' +
    '  gl_FragColor = u_Color;\n' +
    '}\n';
  return {
    vshader: VSHADER_SOURCE,
    fshader: FSHADER_SOURCE
  };
}

2. 创建并使用程序

initShaders这部分是WebGL绘制流程中通用的步骤，不进行过多的解释，主要有以下7个步骤。

创建着色器对象：gl.createShader(type)
填充着色器源代码：gl.shaderSource(shader, source)
编译着色器：gl.compileShader(shader)
创建程序对象：gl.createProgram()
为程序对象分配着色器：gl.attachShader(program, shader) // 注：顶点着色器、片元着色器需要分别分配
连接程序对象：gl.linkProgram(program) // 注：将顶点着色器与片元着色器连接
使用程序对象：gl.useProgram(program)

3. 获取变量位置

至此，我们创建好了一个具有三个属性变量的着色程序，之后我们需要为这三个变量赋值，所以需要获取到这三个变量的存储位置。a_Position和u_MvpMatrix、u_Color的变量声明不同，获取存储位置的方法也相应的不同：

function getLocations() {
  var a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  var u_MvpMatrix = gl.getUniformLocation(gl.program, 'u_MvpMatrix');
  var u_Color = gl.getUniformLocation(gl.program, 'u_Color');
  return {
    a_Position: a_Position,
    u_MvpMatrix: u_MvpMatrix,
    u_Color: u_Color
  };
}

数据缓冲区

因为需要一次性将全部顶点传入顶点着色器，所以需要initVertexBuffers负责创建数据缓冲区并写入数据。

/**
 * 创建缓冲区并传入数据
 * @param {WebGLRenderingContext} gl
 * @param {Float32Array} vertices
 */
function initVertexBuffers(gl, vertices) {
  // 创建缓冲区
  var vertexBuffer = gl.createBuffer();
  if (!vertexBuffer) {
    console.error('Failed to create the buffer object');
    return false;
  }

  // 绑定缓冲区对象：指明其用途
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer);
  // 写入数据
  gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STATIC_DRAW);
  return true;
}

变量赋值

u_MvpMatrix和u_Color变量可直接调用对应类型的方法进行一次传值，比如：

gl.uniformMatrix4fv(locations.u_MvpMatrix, false, mvpMatrix.elements);

WebGLRenderingContext.uniformMatrix[234]fv(location, transpose, value)用于给矩阵类型的变量赋值，2、3、4表示矩阵的维度。

a_Position变量赋值需要从缓冲区中读取数据，需要调用vertexAttribPointer方法将缓冲区对象分配给变量a_Position，并开启访问权：

gl.vertexAttribPointer(locations.a_Position, 3, gl.FLOAT, false, 0, 0);
gl.enableVertexAttribArray(location.a_Position);

其中3表示每个顶点的分量数，a_Position是一个vec4变量，这里读取三个分量的数据赋值给x、y、z，第4位会自动补1。gl.FLOAT表示数据格式为浮点型。false标明无需将数据归一化。最后两个0表示顶点数据间无间隔，数据无偏移。

执行绘制任务

三角剖分步骤中生成了绘制任务tasks = [{mode, start, cnt}, ...]，每个任务指定了模式（TRIANGLE_STRIP/TRIANGLE_FAN/TRIANGLES）、起始点索引值、绘制点数量，所以遍历绘制任务并调用drawArrays进行绘制即可：

tasks.forEach(function(task) {
  gl.drawArrays(gl[task.mode], task.start, task.cnt);
});

至此，绘制线的流程就结束了。

demo演示

利用上文中构造的Shape类，最终实现了如下的demo，绘制了一条S折线，并且可以动态改变其颜色、宽度、端头、拐角样式，同时通过键盘方向键控制Camera，动态改变视图投影矩阵。

webgl绘制基本图形-线