RNN：循环序列模型

序列模型应用领域：
语音识别
音乐发生器
情感分类
DNA序列分析
机器翻译
视频动作识别
命名实体识别

数学符号（识别句子中名字的应用）：

输入句子为x，输出为y,输入句子中每个单词用$x^{<1>},x^{<2>},x^{<3>}...x^{<t>}...x^{<n>}$表示，y同理。y 中有人名的位置用1表示，无用0。

用 Tx 表示输入序列的长度，用 Ty 表示输出序列的长度，两者可等可不等。

用$x^{(i)<t>}$表示第i个输入序列样本中的第t个元素，$T_x^{(i)}$表示第i个输入序列样本的长度, y 同理。

one hot 编码：单个单词的表示方法以及$x^{<t>}$真正对应的是什么。

创建词汇表(Vocabulary)或者字典(Dictionary)来存放一系列（百万级别）的单词，每个单词对应一个索引值。$x^{<t>}$就是一个one hot数组，这个数组的长度就是对应字典或词汇表的长度，$x^{<t>}$这个单词对应的位置在字典或词汇表中数值为1或0，其余皆为0。

如果有的单词没有出现在字典中，可以创建一个新的token（令牌）或者用一个假单词（比如：UKN）来表示。

序列模型不能使用SNN（标准神经网络）原因：

1.不同样本的输入序列长度或输出序列长度不同。即$T_x^{(i)}\ne T_x^{(j)}，T_y^{(i)}\ne T_y^{(j)}$，模型难以统一。

2.标准神经网络结构无法共享序列不同$x^{<t>}$之间的特征。共享特征：如果某个$x^{<t>}$是人名成分，那么句子其它位置出现了，也很可能也是人名。如此以减小模型参数数量。

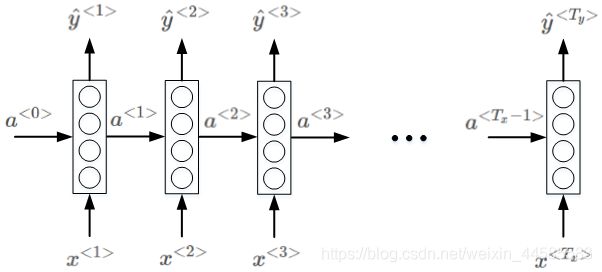
RNN（循环神经网络）：专门处理与时间相关的序列数据（有时间先后的数据）。

时间步长（time step）：语言是逐个生成的，包含时间的概念，使用它的激活函数值$a^{<t>}$向后传递，解决了SNN中参数不能共享的缺点，从而对于处理一整句话这种前后关联性很强的数据样本有很强的优势。

第0个时间步长的激活函数值$a^{<0>}$,作为一个假数据，初始化为全0的向量。

from IPython.display import Image
libo="C:/Users/libo/Desktop/machine learning/序列模型/图片/"
Image(filename = libo + "1.png", width=500, height=100)

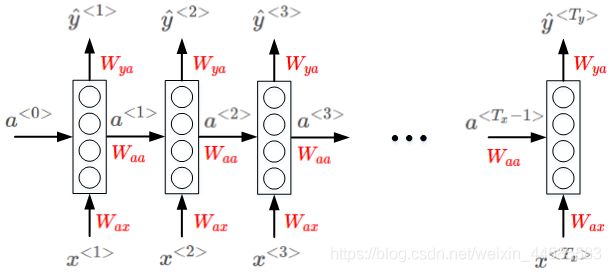
权重系数：

Wax：表示在每个时间步长中从输入层到隐藏层之间的权重参数

Waa：表示在每个时间步长中从前往后共享信息之间的权重参数

Wya：表示在每个时间步长中从隐藏层到输出层之间的权重参数

不同元素之间同一位置共享同一权重系数。

libo="C:/Users/libo/Desktop/machine learning/序列模型/图片/"
Image(filename = libo + "2.png", width=500, height=100)

这个结构的缺点：共享的参数是单向传递的（图中所示是从左往右），这样就只能利用句子中前面的信息往后来进行预测而不能利用后面的信息往前作出预测。

#RNN中的前向传播：
libo="C:/Users/libo/Desktop/machine learning/序列模型/图片/"
Image(filename = libo + "3.png", width=400, height=60)

RNN中的反向传播（时间反向传播）：

单样本上的损失函数：
$L^{<t>}({\hat{y}}^{<t>},y^{<t>})=-y^{<t>}log({\hat{y}}^{<t>})-(1-y^{<t>})log(1-{\hat{y}}^{<t>})$
运用这个公式，就可以在每个时间步长上计算单个样本上的损失。

全样本上的成本函数：
$L(\hat{y},y)=\sum (L^{<t>}({\hat{y}}^{<t>},y^{<t>}))$
计算完单个样本上的损失，再相加得到全样本上的损失总和。

均方差MSE：$MSE(y,\acute{y})=\frac{{\sum }_{i=1}^n(y_i-{\acute{y}}_i{)}^2}{n}$

RNN的不同类型：

many-to-many 模型：名字主体识别，输入输出长度为多，但不一定完全相等。

many-to-one 模型：情感分类，根据输入的内容进行分类，输出一个0-5之间的整数评分。

one-to-many 模型：音乐生成，输入一个整数，模型会根据这个整数输出一段音乐，前一个输出的预测值也会被用于下一个预测中。

语言模型：在语音识别中，对于输入两个相似发音的句子，通常会用语言模型来分别判断输出这两个句子的概率，概率高的句子就会被输出。

语言模型的构建：

1.数据集：大量文本的语料库

2.对文本进行Tokenize令牌化：在创建的字典或词汇表时，对每个单词分别进行one
hot处理，在句末添加一个额外的EOS（End Of Sentence）token，表示一个句子的结束。也要考虑是否将句号等标点符号也作为一个token。对于没有出现在字典或词汇表中的单词，则添加 UKN 作为token。

3.构建基本的RNN模型。

libo="C:/Users/libo/Desktop/machine learning/序列模型/图片/"
Image(filename = libo + "5.png", width=500, height=60)

语言模型的RNN结构如上图所示，$x^{<1>}和a^{<0>}$均为零向量。Softmax输出层${\hat{y}}^{<1>}$表示出现该语句第一个单词的概率，softmax输出层${\hat{y}}^{<2>}$表示在第一个单词基础上出现第二个单词的概率，即条件概率，以此类推，最后是出现< EOS >的条件概率。计算完预测值，再计算损失，并用之来训练网络。RNN学会从前往后依次地预测单词。

单个元素的softmax loss function为：

$L^{<t>}({\hat{y}}^{<t>},y^{<t>})=-{\sum }_i{y}_i^{<t>}log{\hat{y}}_i^{<t>}$

该样本所有元素的Loss function为：

$L(\hat{y},y)={\sum }_t{L}^{<t>}({\hat{y}}^{<t>},y^{<t>})$

对语料库的每条语句进行RNN模型训练，最终得到的模型可以根据给出语句的前几个单词预测其余部分，将语句补充完整。

整个语句出现的概率等于语句中所有元素出现的条件概率乘积。

利用训练好的RNN语言模型，可以进行新的序列采样，从而随机产生新的语句。

首先，从第一个元素输出${\hat{y}}^{<1>}$的softmax分布中随机选取一个word作为新语句的首单词$y^{<1>}$。然后，$y^{<1>}$作为$x^{<2>}$。从中选取概率最大的word作为$y^{<2>}$，继续将$y^{<2>}$作为$x^{<3>}$，以此类推。直到产生< EOS >结束符，则标志语句生成完毕。

如果不希望新的语句中包含< UNK >标志符，可以在每次产生< UNK >时重新采样，直到生成非< UNK >标志符为止。

以上介绍的是word level RNN，即每次生成单个word，语句由多个words构成。另外一种情况是character level RNN.

从已训练的RNN中采样生成新序列：把前一个时间步长产生的预测值当成下一个时间步长开始的输入值。

字符级语言模型(character-level language model)：前面讲到的都是词级语言模型(word-level language model)，字符级语言模型不再是创建包含单词的字典而是创建包含大小写字母，标点，空格等元素的字典。又因为每个单词都是由字母组成的，这时候就无需像词级语言模型一样另外为字典中不包含的单词和标点创建Token。避免了不存在的单词–< UNK>

字符级序列模型的主要缺点：组建的序列往往会很长，会造成字符级语言模型在获取长范围的句子前后依赖关系上比不上词级语言模型，并且在训练时会很耗费计算。

RNN的梯度消失：RNN在训练时，也会出现梯度消失或者梯度爆炸。

梯度爆炸：对模型重新进行梯度修剪(gradient clipping)就能避免问题。设定一个阈值，一旦梯度最大值达到这个阈值，就对整个梯度向量进行尺度缩小。
梯度消失：GRU和LSTM

#RNN的隐藏层单元结构
libo="C:/Users/libo/Desktop/machine learning/序列模型/图片/"
Image(filename = libo + "6.png", width=300, height=60)

a的表达式为：

$a^{<t>}=tanh(W_a[a^{<t-1>},x^{<t>}]+b_a)$

为了解决梯度消失问题，对上述单元进行修改，添加了记忆单元，构建GRU。GRN(Gated Recurrent Units)：组成RNN隐藏层的部分，不仅能够帮助RNN更好地捕获长范围的连接关系，还对梯度消失问题有帮助。如下图所示：

libo="C:/Users/libo/Desktop/machine learning/序列模型/图片/"
Image(filename = libo + "7.png", width=400, height=60)

在GRU中，提出memory cell(记忆细胞)的概念，用c来表示。c的作用就是记住一些需要记忆的信息。在GRU的概念中，$c^{<t>}=a^{<t>}$，即记忆细胞的值是和激活函数的输出值相等的。

在每个时间步长中，我们重新定义一个候选项：${\tilde{c}}^{<t>}=tanh(w_c[c^{<t-1>},x^{<t>}]+b_c)$ ,然后定义更新门$\Gamma u=\sigma (w_u[c^{<t-1>},x^{<t>}]+b_u)$ ，下标u表示update的意思，有时也用Gu表示。因为Γu 取0到1的范围，所以用上sigmoid激活函数来使计算结果在0到1的范围内。

具体操作中，用${\tilde{c}}^{<t>}$来更新$c^{<t>}$。

即用下面这个公式$c_t=\Gamma u\ast {\tilde{c}}^{<t>}+(1-\Gamma u)\ast c^{<t-1>}$。

当Γu=1时，$c^{<t>}$更新为备选项${\tilde{c}}^{<t>}$；

当Γu=0时，$c^{<t>}=c^{<t-1>}$

更新门可以控制过去的信息在当前时刻的重要性。如果更新门一直近似1，过去的信息将一直通过时间保存并传递至当前时刻。GRU的这个设计可以应对RNN中的梯度衰减问题，并且更好地捕获长范围内前后信息的依赖关系。

对门控循环单元的设计稍作总结：

Γr门有助于捕捉序列数据中短期的依赖关系。
Γu门有助于捕捉序列数据中长期的依赖关系。

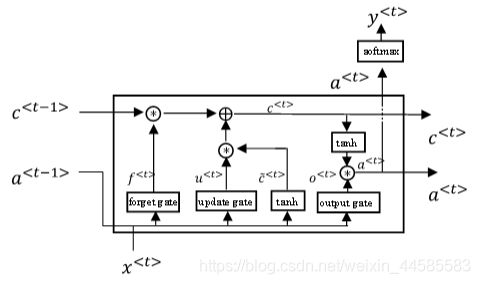
长短时记忆(LSTM):LSTM比GRU复杂，它使用了三个gate。且在LSTM(Long Short Term Memory)中，$c^{<t>}$和$a^{<t>}$不再是对等的。

libo="C:/Users/libo/Desktop/machine learning/序列模型/图片/"
Image(filename = libo + "8.png", width=400, height=60)

计算当前记忆细胞结合了上一时刻记忆细胞和当前时刻候选记忆细胞的信息，并通过遗忘门Γf 和更新门Γu 来控制信息的流动。当Γf 近似1而Γu 近似0时，过去时刻的信息一直通过时间保存下来，而当前信息则被丢弃遗忘。

传入下一时刻的激活值（或者称为隐藏信息）：
$a^{<t>}=\Gamma o\ast tanh{c}^{<t>}$

隐藏信息的流动取决于输出门Γo ，当Γo 近似为1时，信息被传递到下一时刻；当Γo 近似为0时，细胞信息自己保留。

libo="C:/Users/libo/Desktop/machine learning/序列模型/图片/"
Image(filename = libo + "9.png", width=400, height=60)

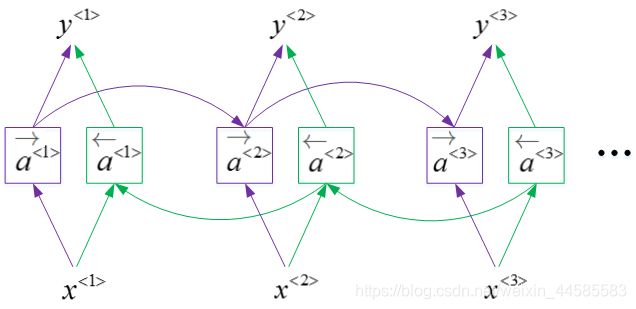
双向RNN（BRNN）：在单向RNN的基础上，添加一个反向循环层（图中绿线），反向层计算的也是激活函数。

BRNN对应的输出yy表达式为：

${\hat{y}}^{<t>}=g(W_y[a^{\to <t>},a^{\leftarrow <t>}]+b_y)$

BRNN能够同时对序列进行双向处理，性能大大提高。但是计算量较大，且要知道全部信息才能反向向前预测。

libo="C:/Users/libo/Desktop/machine learning/序列模型/图片/"
Image(filename = libo + "10.png", width=400, height=60)

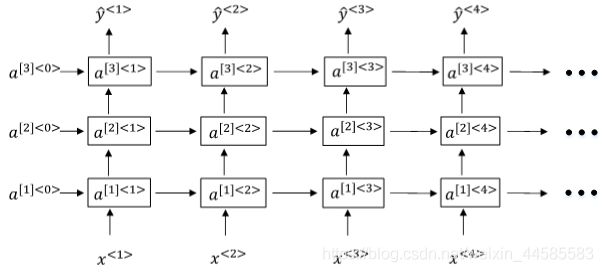
Deep RNNs：与DNN一样，用上标[l]表示层数。Deep RNNs中$a^{[l]<t>}$的表达式为：

$a^{[l]<t>}=g(W_a^{[l]}[a^{[l]<t-1>},a^{[l-1]<t>}]+b_a^{[l]})$

libo="C:/Users/libo/Desktop/machine learning/序列模型/图片/"
Image(filename = libo + "11.png", width=400, height=60)