数据结构--线段树

描述

线段树是一种非常灵活的数据结构，它可以用于解决多种范围查询问题，比如在对数时间内从数组中找到最小值、最大值、总和、最大公约数、最小公倍数等。

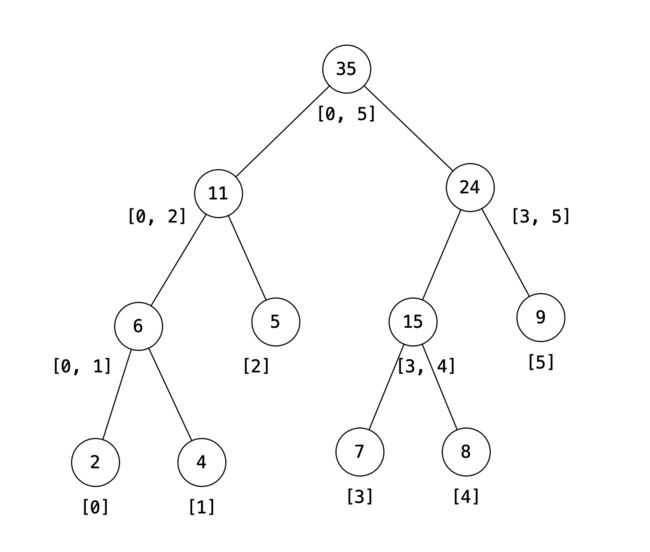
数组 A[0,1,…,n−1] 的线段树是一个二叉树，其中每个节点都包含数组的一个子范围 [i…j] 上的聚合信息（最小值、最大值、总和等），其左、右子节点分别包含范围 [i…$\frac{i+j}{2}$] 和 [$\frac{i+j}{2}+1$, j]上的信息。

线段树既可以用数组也可以用树来实现。对于数组实现，如果索引 ii 处的元素不是一个叶节点，那么其左子节点和右子节点分别存储在索引为 2i 和 2i+1的元素处。

在上图所给出的示例中，每个叶节点都包含初始的数组元素 {2,4,5,7,8,9}。内部节点包含范围内相应元素的总和 - (11) 是从索引 0 到索引 2 的元素之和。而根节点 (35) 是它的两个子节点 (6) 和 (29) 的和,也是整个数组的和。

线段树可以分为以下三个步骤：

• 从给定数组构建线段树的预处理步骤。
• 修改元素时更新线段树。
• 使用线段树进行区域和检索。

上面解释复制于 https://leetcode-cn.com/problems/range-sum-query-mutable/solution/qu-yu-he-jian-suo-shu-zu-ke-xiu-gai-by-leetcode/

307 区域和检索 - 数组可修改

给你一个数组 nums ，请你完成两类查询，其中一类查询要求更新数组下标对应的值，另一类查询要求返回数组中某个范围内元素的总和。
实现 NumArray 类：
NumArray(int[] nums) 用整数数组 nums 初始化对象
void update(int index, int val) 将 nums[index] 的值更新为 val
int sumRange(int left, int right) 返回子数组 nums[left, right] 的总和（即，nums[left] + nums[left + 1], …, nums[right]）

示例：

输入：
[“NumArray”, “sumRange”, “update”, “sumRange”]
[[[1, 3, 5]], [0, 2], [1, 2], [0, 2]]
输出：
[null, 9, null, 8]
解释：
NumArray numArray = new NumArray([1, 3, 5]);
numArray.sumRange(0, 2); // 返回 9 ，sum([1,3,5]) = 9
numArray.update(1, 2); // nums = [1,2,5]
numArray.sumRange(0, 2); // 返回 8 ，sum([1,2,5]) = 8

提示：
1 <= nums.length <= 3 * 104
-100 <= nums[i] <= 100
0 <= index < nums.length
-100 <= val <= 100
0 <= left <= right < nums.length
最多调用 3 * 104 次 update 和 sumRange 方法

class NumArray {
    private int[] nums;
    private int[] sum;
    public NumArray(int[] nums) {
        this.nums = nums;
        sum = new int[nums.length * 4];
        buildTree(0,nums.length-1,0);
    }

    public void update(int index, int val) {
        update(0,nums.length-1,0,index,val);
        nums[index] = val;
    }


    public int sumRange(int left, int right) {
        return query(0,nums.length-1,0,left,right);
    }

    /**
     * 创建树
     * @param left 数据左边界
     * @param right 数据右边界
     * @param index 数据开始位置
     */
    public void buildTree(int left, int right, int index) {
        if (left == right) {
            sum[index] = nums[left];
            return;
        }
        int middle = ((right - left) >> 1) + left;
        buildTree(left, middle, index << 1 | 1);
        buildTree(middle+1, right, (index << 1) + 2);
        pushUp(index);
    }

    public void pushUp(int index) {
        sum[index] = sum[index << 1 | 1] + sum[(index << 1) + 2];
    }

    /**
     * 单个位置更新操作
     * @param left 数据左边界
     * @param right 数据有边界
     * @param index 数据开始位置
     * @param position 更改的位置
     * @param val 更改的值
     */
    public void update(int left,int right,int index,int position,int val){
        if (left == right){
            sum[index] += val - nums[position];
            return;
        }
        int middle = ((right - left) >> 1) + left;
        if (position <= middle){
            update(left,middle,index<<1|1,position,val);
        }else {
            update(middle+1,right,(index << 1) + 2,position,val);
        }
        pushUp(index);
    }

    /**
     * 查询区间值的和
     * @param left 整个区间的最左边
     * @param right 整个区间的最右边
     * @param index 0
     * @param queryLeft 查询的区间左边
     * @param queryRight 查询的区间右边
     * @return 返回和值
     */
    public int query(int left,int right,int index,int queryLeft,int queryRight) {
        if (left == queryLeft && right == queryRight) {
            return sum[index];
        }
        int middle = ((right - left) >> 1) + left;
        if (queryLeft >= middle + 1) {
            return query(middle + 1, right, (index << 1) + 2, queryLeft, queryRight);
        } else if (queryRight <= middle){
            return query(left, middle, index << 1 | 1, queryLeft, queryRight);
        }
        int leftResult = query(left, middle, index << 1 | 1, queryLeft, middle);
        int rightResult = query(middle + 1, right, (index << 1) + 2, middle+1, queryRight);
        return leftResult+rightResult;
    }

}