同DataWhale一起组队学习:https://tianchi.aliyun.com/notebook-ai/detail?spm=5176.12281978.0.0.6802593a2HCrSE&postId=95457
EDA 即 Exploratory Data Analysis,当我们拿到数据之后,需要对数据本身有一个直观的理解比如各项统计值:最大值,最小值,中位数,均值,方差,偏移度,丰度等等,这些指标可以帮助我们跨快速的浏览数据的样貌,获得一个大体的认知。
EDA的价值主要在于熟悉数据集,了解数据集,对数据集进行验证来确定所获得数据集可以用于接下来的机器学习或者深度学习使用。
当了解了数据集之后我们下一步就是要去了解变量间的相互关系以及变量与预测值之间的存在关系。
引导数据科学从业者进行数据处理以及特征工程的步骤,使数据集的结构和特征集让接下来的预测问题更加可靠。
内容介绍
通常情况下,我们会利用一些常用的数据科学库pandas、numpy、scipy和常用的可视化库 matplotlib、seabon,利用这些库里面的函数可以帮助我们快速的计算和展示数据集的特性。在EDA阶段,大概有以下几个过程:
- 载入数据:
- 载入训练集和测试集;
- 简略观察数据(head()+shape);
- 数据总览:
- 通过describe()来熟悉数据的相关统计量
- 通过info()来熟悉数据类型
- 判断数据缺失和异常
- 查看每列的存在nan情况,由于有时数据中会用一些约定的填充来表示nan,那这是就需要我们去主动统计数据的值
- 异常值检测,可以使用箱线图去检测异常值
- 了解预测值的分布:
- 总体分布概况(无界约翰逊分布等),一般希望预测值属于正态分布,如果不是正太分布,则需要将它转为正太分布,因为使用线性回归需要满足误差项属于正态分布。这时,我们可以使用 变换,使标签贴近于正态分布。回归分析的五个基本假设,特征工程——转换为正态分布
- 查看skewness and kurtosis ,skewness 是偏度,kurtosis 是丰度,峰度系数是用来反映频数分布曲线顶端尖峭或扁平程度的指标。有时两组数据的算术平均数、标准差和偏态系数都相同,但他们分布曲线顶端的高耸程度却不同。 偏度系数是描述分布偏离对称性程度的一个特征数。当分布左右对称时,偏度系数为0。当偏度系数大于0时,即重尾在右侧时,该分布为右偏。当偏度系数小于0时,即重尾在左侧时,该分布左偏。
- 查看预测值的具体频数
- 特征分为类别特征和数字特征,并对类别特征查看unique分布
- 数字特征分析
- 相关性分析,关于相关性分析可以看pandas相关性分析,相关系数则是由协方差除以两个变量的标准差而得
- 查看几个特征得 偏度和峰值
- 每个数字特征得分布可视化
- 数字特征相互之间的关系可视化
- 多变量互相回归关系可视化
- 类型特征分析
- unique分布
- 类别特征箱形图可视化
- 类别特征的小提琴图可视化
- 类别特征的柱形图可视化类别
- 特征的每个类别频数可视化(count_plot)
- 用pandas_profiling生成数据报告
代码案例
下面是天池新人赛中datawhale提供的解析代码,Datawhale 零基础入门数据挖掘-Task2 数据分析
#coding:utf-8
#导入warnings包,利用过滤器来实现忽略警告语句。
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import missingno as msno
可以使用pandas载入csv文件数据
## 通过Pandas对于数据进行读取 (pandas是一个很友好的数据读取函数库)
Train_data = pd.read_csv('datalab/used_car_train_20200313.csv', sep=' ')
TestA_data = pd.read_csv('datalab/used_car_testA_20200313.csv', sep=' ')
## 输出数据的大小信息
print('Train data shape:',Train_data.shape)
print('TestA data shape:',TestA_data.shape)
Train data shape: (150000, 31)
TestA data shape: (50000, 30)
所有特征集及其含义
- name - 汽车编码
- regDate - 汽车注册时间
- model - 车型编码
- brand - 品牌
- bodyType - 车身类型
- fuelType - 燃油类型
- gearbox - 变速箱
- power - 汽车功率
- kilometer - 汽车行驶公里
- notRepairedDamage - 汽车有尚未修复的损坏
- regionCode - 看车地区编码
- seller - 销售方
- offerType - 报价类型
- creatDate - 广告发布时间
- price - 汽车价格
- v_0', 'v_1', 'v_2', 'v_3', 'v_4', 'v_5', 'v_6', 'v_7', 'v_8', 'v_9', 'v_10', 'v_11', 'v_12', 'v_13','v_14' 【匿名特征,包含v0-14在内15个匿名特征】
pandas_profiling简单处理
探索数据有一个简单的工具pandas_profiling,如果只是粗略了解,这个也是可以的。
但是实际使用的时候速度很慢,而且网页加载打开的时候卡顿严重,所以还是谨慎使用
import pandas_profiling
pfr = pandas_profiling.ProfileReport(Train_data)
pfr.to_file("./example.html")
数据总览
Train_data.describe()
| SaleID | name | regDate | ... | v_14 |
|---|---|---|---|---|
| count | 150000.000000 | 150000.000000 | ... | 150000.000000 |
| mean | 74999.500000 | 68349.172873 | ... | 0.000313 |
| std | 43301.414527 | 61103.875095 | ... | 1.288988 |
| min | 0.000000 | 0.000000 | ... | -4.153899 |
| 25% | 37499.750000 | 11156.000000 | ... | -1.057789 |
| 50% | 74999.500000 | 51638.000000 | ... | -0.036245 |
| 75% | 112499.250000 | 118841.250000 | ... | 0.942813 |
| max | 149999.000000 | 196812.000000 | ... | 11.147669 |
Train_data.info()
RangeIndex: 150000 entries, 0 to 149999
Data columns (total 31 columns):
SaleID 150000 non-null int64
name 150000 non-null int64
regDate 150000 non-null int64
model 149999 non-null float64
brand 150000 non-null int64
bodyType 145494 non-null float64
fuelType 141320 non-null float64
gearbox 144019 non-null float64
power 150000 non-null int64
kilometer 150000 non-null float64
notRepairedDamage 150000 non-null object
regionCode 150000 non-null int64
seller 150000 non-null int64
offerType 150000 non-null int64
creatDate 150000 non-null int64
price 150000 non-null int64
v_0 150000 non-null float64
v_1 150000 non-null float64
v_2 150000 non-null float64
v_3 150000 non-null float64
v_4 150000 non-null float64
v_5 150000 non-null float64
v_6 150000 non-null float64
v_7 150000 non-null float64
v_8 150000 non-null float64
v_9 150000 non-null float64
v_10 150000 non-null float64
v_11 150000 non-null float64
v_12 150000 non-null float64
v_13 150000 non-null float64
v_14 150000 non-null float64
dtypes: float64(20), int64(10), object(1)
memory usage: 35.5+ MB
缺失值处理
对于缺失值的处理,有时候,缺失值可以使用pandas去统计,但是实际上,有的缺失值在录入表格的时候,用了别的作为替代,这时要找到它并换过来
Train_data.isnull().sum()
output
SaleID 0
name 0
regDate 0
model 1
brand 0
bodyType 4506
fuelType 8680
gearbox 5981
power 0
kilometer 0
notRepairedDamage 0
regionCode 0
seller 0
offerType 0
creatDate 0
price 0
v_0 0
v_1 0
v_2 0
v_3 0
v_4 0
v_5 0
v_6 0
v_7 0
v_8 0
v_9 0
v_10 0
v_11 0
v_12 0
v_13 0
v_14 0
dtype: int64
由于notRepairedDamage是object类型,那么他有可能存在非标准的缺失值,事实上应该每一个特征列都查找一遍,以确保没有遗漏
Train_data['notRepairedDamage'].value_counts()
output
0.0 111361
- 24324
1.0 14315
Name: notRepairedDamage, dtype: int64
可以看到这里确实有一个缺失值填充的符号,我们需要将它换回来
Train_data['notRepairedDamage'].replace('-', np.nan, inplace=True)
Train_data.isnull().sum()
output
SaleID 0
name 0
regDate 0
model 1
brand 0
bodyType 4506
fuelType 8680
gearbox 5981
power 0
kilometer 0
notRepairedDamage 24324
regionCode 0
seller 0
offerType 0
creatDate 0
price 0
v_0 0
v_1 0
v_2 0
v_3 0
v_4 0
v_5 0
v_6 0
v_7 0
v_8 0
v_9 0
v_10 0
v_11 0
v_12 0
v_13 0
v_14 0
dtype: int64
这时notRepairedDamage缺失值数目其实最多
异常特征
还有一些特征异常倾斜,就是大多数集中在某个数值上面,这些特征也没有太大价值
Train_data["seller"].value_counts()
output
0 149999
1 1
Name: seller, dtype: int64
Train_data["offerType"].value_counts()
output
0 150000
Name: offerType, dtype: int64
这两个特征基本没有价值
标签探索
简单探索完特征之后,再来探索下需要预测的标签数值price
Train_data['price'].value_counts()
output
500 2337
1500 2158
1200 1922
1000 1850
2500 1821
...
25321 1
8886 1
8801 1
37920 1
8188 1
Name: price, Length: 3763, dtype: int64
标签分布
我们要探究一下标签数值price服从什么分布,我们通常需要将偏态分布转换成正态分布,可以更好的帮助机器学习到有价值的信息
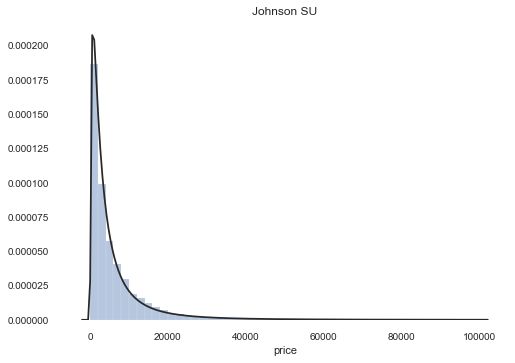
## 1) 总体分布概况(无界约翰逊分布等)
import scipy.stats as st
y = Train_data['price']
plt.figure(1); plt.title('Johnson SU')
sns.distplot(y, kde=False, fit=st.johnsonsu)
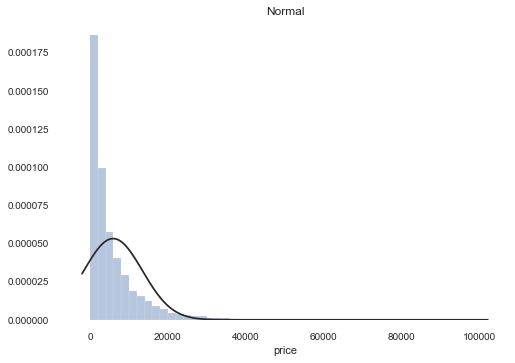
plt.figure(2); plt.title('Normal')
sns.distplot(y, kde=False, fit=st.norm)
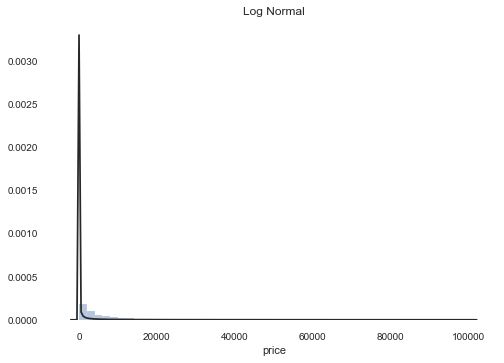
plt.figure(3); plt.title('Log Normal')
sns.distplot(y, kde=False, fit=st.lognorm)
output
标签与特征的相关性
特征分为数值特征和分类特征,数值特征好理解,而分类特征则指的是离散的类别特征
numeric_features = ['power', 'kilometer', 'v_0', 'v_1', 'v_2', 'v_3', 'v_4', 'v_5', 'v_6', 'v_7', 'v_8', 'v_9', 'v_10', 'v_11', 'v_12', 'v_13','v_14' ]
categorical_features = ['name', 'model', 'brand', 'bodyType', 'fuelType', 'gearbox', 'notRepairedDamage', 'regionCode',]
我们可以去利用pandas获各数值特征与类别标签的相关性分析
numeric_features.append('price')
price_numeric = Train_data[numeric_features]
correlation = price_numeric.corr()
print(correlation['price'].sort_values(ascending = False),'\n')
output
price 1.000000
v_12 0.692823
v_8 0.685798
v_0 0.628397
power 0.219834
v_5 0.164317
v_2 0.085322
v_6 0.068970
v_1 0.060914
v_14 0.035911
v_13 -0.013993
v_7 -0.053024
v_4 -0.147085
v_9 -0.206205
v_10 -0.246175
v_11 -0.275320
kilometer -0.440519
v_3 -0.730946
Name: price, dtype: float64
这里也可以使用热力图去查看相关性
f , ax = plt.subplots(figsize = (7, 7))
plt.title('Correlation of Numeric Features with Price',y=1,size=16)
sns.heatmap(correlation,square = True, vmax=0.8)
output
del price_numeric['price']
特征可视化
数值特征
特征的偏度和峰值
for col in numeric_features:
print('{:15}'.format(col),
'Skewness: {:05.2f}'.format(Train_data[col].skew()) ,
' ' ,
'Kurtosis: {:06.2f}'.format(Train_data[col].kurt())
)
power Skewness: 65.86 Kurtosis: 5733.45
kilometer Skewness: -1.53 Kurtosis: 001.14
v_0 Skewness: -1.32 Kurtosis: 003.99
v_1 Skewness: 00.36 Kurtosis: -01.75
v_2 Skewness: 04.84 Kurtosis: 023.86
v_3 Skewness: 00.11 Kurtosis: -00.42
v_4 Skewness: 00.37 Kurtosis: -00.20
v_5 Skewness: -4.74 Kurtosis: 022.93
v_6 Skewness: 00.37 Kurtosis: -01.74
v_7 Skewness: 05.13 Kurtosis: 025.85
v_8 Skewness: 00.20 Kurtosis: -00.64
v_9 Skewness: 00.42 Kurtosis: -00.32
v_10 Skewness: 00.03 Kurtosis: -00.58
v_11 Skewness: 03.03 Kurtosis: 012.57
v_12 Skewness: 00.37 Kurtosis: 000.27
v_13 Skewness: 00.27 Kurtosis: -00.44
v_14 Skewness: -1.19 Kurtosis: 002.39
price Skewness: 03.35 Kurtosis: 019.00
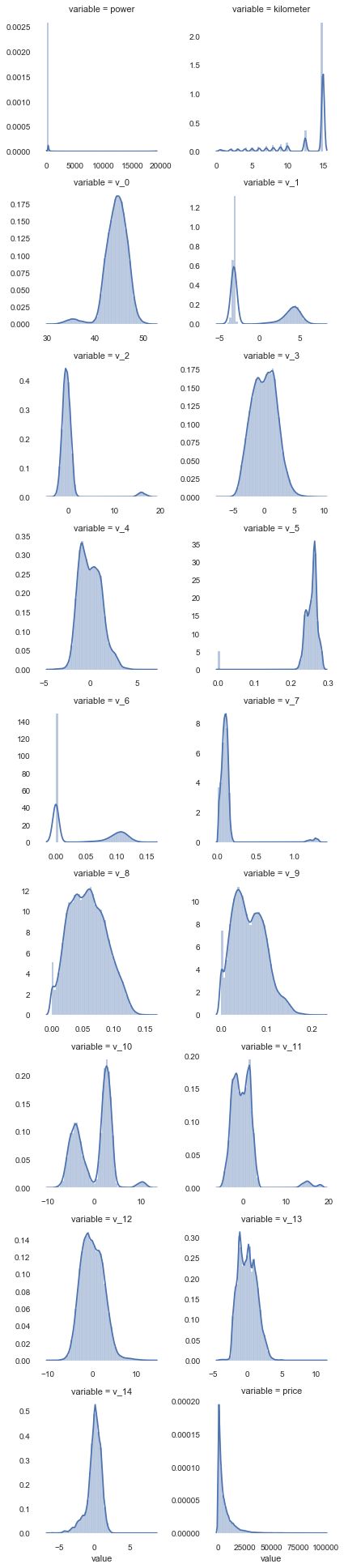
数字特征得分布可视化
f = pd.melt(Train_data, value_vars=numeric_features)
g = sns.FacetGrid(f, col="variable", col_wrap=2, sharex=False, sharey=False)
g = g.map(sns.distplot, "value")
数字特征相互之间的关系可视化
sns.set()
columns = ['price', 'v_12', 'v_8' , 'v_0', 'power', 'v_5', 'v_2', 'v_6', 'v_1', 'v_14']
sns.pairplot(Train_data[columns],size = 2 ,kind ='scatter',diag_kind='kde')
plt.show()
此处是多变量之间的关系可视化,可视化更多学习可参考很不错的文章 https://www.jianshu.com/p/6e18d21a4cad
Y_train = Train_data['price']
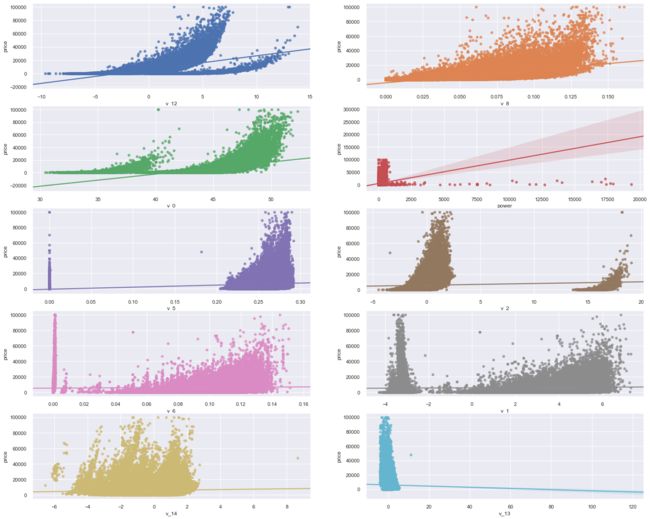
## 5) 多变量互相回归关系可视化
fig, ((ax1, ax2), (ax3, ax4), (ax5, ax6), (ax7, ax8), (ax9, ax10)) = plt.subplots(nrows=5, ncols=2, figsize=(24, 20))
# ['v_12', 'v_8' , 'v_0', 'power', 'v_5', 'v_2', 'v_6', 'v_1', 'v_14']
v_12_scatter_plot = pd.concat([Y_train,Train_data['v_12']],axis = 1)
sns.regplot(x='v_12',y = 'price', data = v_12_scatter_plot,scatter= True, fit_reg=True, ax=ax1)
v_8_scatter_plot = pd.concat([Y_train,Train_data['v_8']],axis = 1)
sns.regplot(x='v_8',y = 'price',data = v_8_scatter_plot,scatter= True, fit_reg=True, ax=ax2)
v_0_scatter_plot = pd.concat([Y_train,Train_data['v_0']],axis = 1)
sns.regplot(x='v_0',y = 'price',data = v_0_scatter_plot,scatter= True, fit_reg=True, ax=ax3)
power_scatter_plot = pd.concat([Y_train,Train_data['power']],axis = 1)
sns.regplot(x='power',y = 'price',data = power_scatter_plot,scatter= True, fit_reg=True, ax=ax4)
v_5_scatter_plot = pd.concat([Y_train,Train_data['v_5']],axis = 1)
sns.regplot(x='v_5',y = 'price',data = v_5_scatter_plot,scatter= True, fit_reg=True, ax=ax5)
v_2_scatter_plot = pd.concat([Y_train,Train_data['v_2']],axis = 1)
sns.regplot(x='v_2',y = 'price',data = v_2_scatter_plot,scatter= True, fit_reg=True, ax=ax6)
v_6_scatter_plot = pd.concat([Y_train,Train_data['v_6']],axis = 1)
sns.regplot(x='v_6',y = 'price',data = v_6_scatter_plot,scatter= True, fit_reg=True, ax=ax7)
v_1_scatter_plot = pd.concat([Y_train,Train_data['v_1']],axis = 1)
sns.regplot(x='v_1',y = 'price',data = v_1_scatter_plot,scatter= True, fit_reg=True, ax=ax8)
v_14_scatter_plot = pd.concat([Y_train,Train_data['v_14']],axis = 1)
sns.regplot(x='v_14',y = 'price',data = v_14_scatter_plot,scatter= True, fit_reg=True, ax=ax9)
v_13_scatter_plot = pd.concat([Y_train,Train_data['v_13']],axis = 1)
sns.regplot(x='v_13',y = 'price',data = v_13_scatter_plot,scatter= True, fit_reg=True, ax=ax10)
output
类别特征分布
unique分布
查看哪些类别特征有价值,如果每个样本都一个不一样的类别,那这个类别特征太稀疏了,没什么价值
for fea in categorical_features:
print(Train_data[fea].nunique())
99662
248
40
8
7
2
2
7905
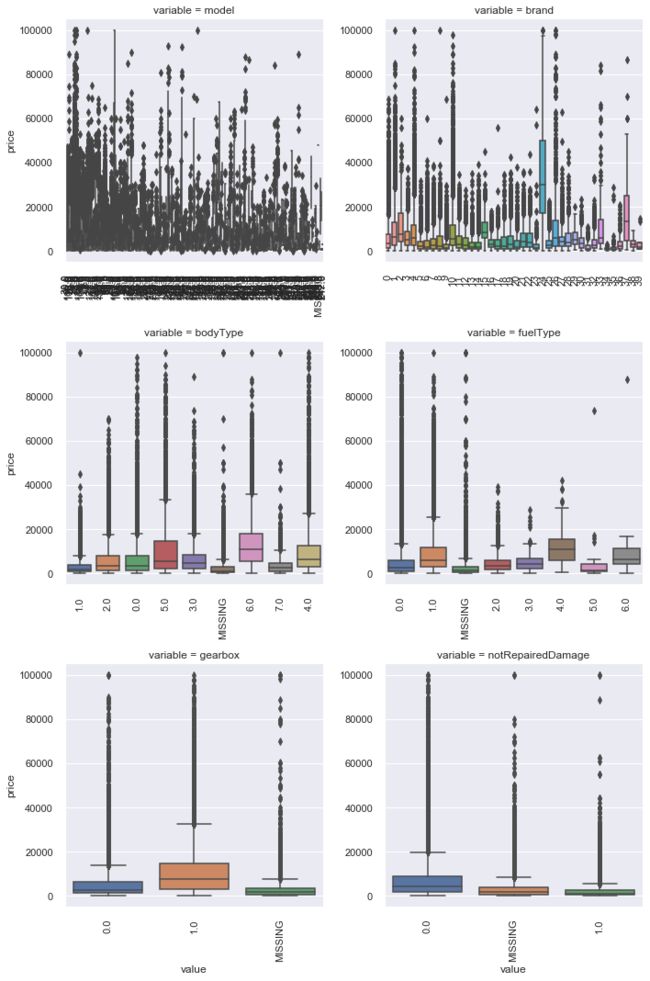
类别特征箱形图可视化
# 因为 name和 regionCode的类别太稀疏了,这里我们把不稀疏的几类画一下
categorical_features = ['model',
'brand',
'bodyType',
'fuelType',
'gearbox',
'notRepairedDamage']
for c in categorical_features:
Train_data[c] = Train_data[c].astype('category')
if Train_data[c].isnull().any():
Train_data[c] = Train_data[c].cat.add_categories(['MISSING'])
Train_data[c] = Train_data[c].fillna('MISSING')
def boxplot(x, y, **kwargs):
sns.boxplot(x=x, y=y)
x=plt.xticks(rotation=90)
f = pd.melt(Train_data, id_vars=['price'], value_vars=categorical_features)
g = sns.FacetGrid(f, col="variable", col_wrap=2, sharex=False, sharey=False, size=5)
g = g.map(boxplot, "value", "price")
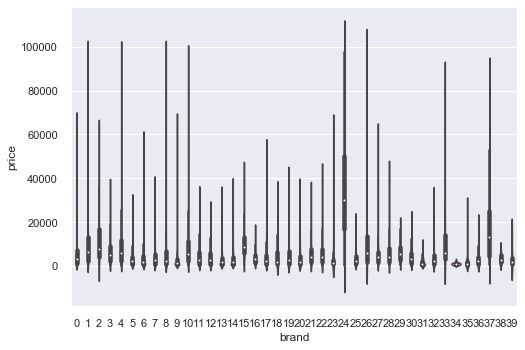
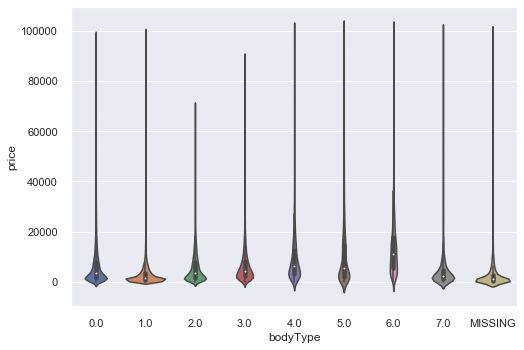
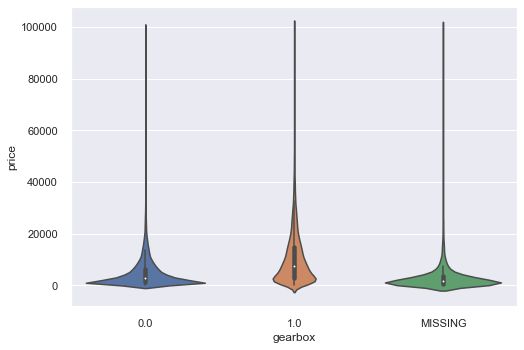
类别特征的小提琴图可视化
catg_list = categorical_features
target = 'price'
for catg in catg_list :
sns.violinplot(x=catg, y=target, data=Train_data)
plt.show()
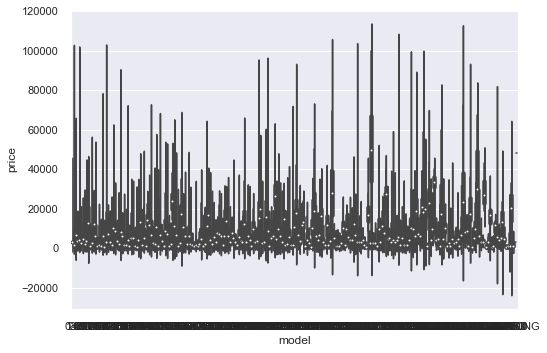
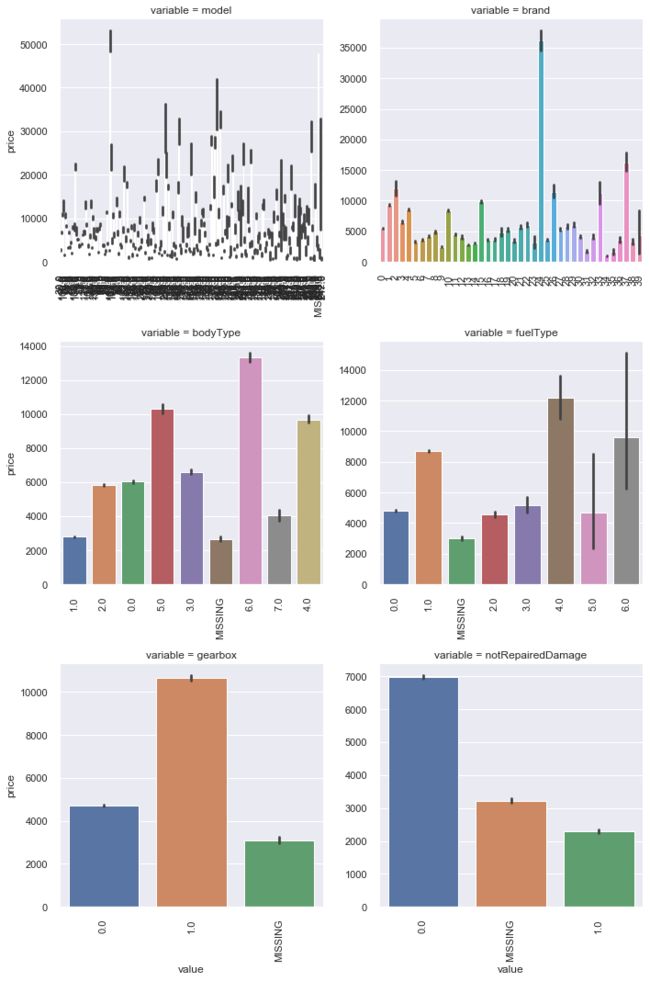
类别特征的柱形图可视化
def bar_plot(x, y, **kwargs):
sns.barplot(x=x, y=y)
x=plt.xticks(rotation=90)
f = pd.melt(Train_data, id_vars=['price'], value_vars=categorical_features)
g = sns.FacetGrid(f, col="variable", col_wrap=2, sharex=False, sharey=False, size=5)
g = g.map(bar_plot, "value", "price")