牛津大学出品:随机噪声对抗训练
引言
该论文出自于牛津大学,主要是关于对抗训练的研究。目前已经有研究表明使用单步 F G S M \mathrm{FGSM} FGSM进行对抗训练会导致一种严重的过拟合现象,在该论文中作者经过理论分析和实验验证重新审视了对抗噪声和梯度剪切在单步对抗训练中的作用。作者发现对于大的对抗扰动半径可有效避免过拟合现象。基于该观察结果,作者提出了一种随机噪声对抗训练 N - F G S M \mathrm{N\text{-}FGSM} N-FGSM,实验表明该方法不仅提供了单步对抗训练的减少计算开销的好处,而且也不会受到过拟合现象的影响。论文里没有提供相关源代码,本文最后一节是关于该论文算法的一个简单实现。
论文链接:https://arxiv.org/abs/2202.01181

预备知识
给定一个参数为 θ \theta θ的分类器 f θ : X → Y f_\theta:\mathcal{X}\rightarrow \mathcal{Y} fθ:X→Y,一个对抗扰动集合 S \mathcal{S} S。如果对于任意的对抗扰动 δ ∈ S \delta\in \mathcal{S} δ∈S,有 f θ ( x + δ ) = f θ ( x ) f_\theta(x+\delta)=f_\theta(x) fθ(x+δ)=fθ(x),则可以说 f θ f_\theta fθ在点 x ∈ X x\in \mathcal{X} x∈X关于对抗扰动集合 S \mathcal{S} S是鲁棒的。对抗扰动集合 S \mathcal{S} S的定义为 S = { δ : ∥ δ ∥ ∞ ≤ ϵ } \mathcal{S}=\{\delta:\|\delta\|_\infty\le \epsilon\} S={δ:∥δ∥∞≤ϵ}为了使得神经网络模型能够在 ℓ ∞ \ell_\infty ℓ∞范数具有鲁棒性。对抗训练在数据集 D = { ( x i , y i ) } i = 1 : N \mathcal{D}=\{(x_i,y_i)\}_{i=1:N} D={(xi,yi)}i=1:N上修正类别训练进程并最小化损失函数,其中对抗训练的目标为 min θ ∑ i = 1 N max δ L ( f θ ( x i + δ ) , y i ) s . t . ∥ δ ∥ ∞ ≤ ϵ \min\limits_{\theta}\sum\limits_{i=1}^N\max\limits_{\delta} \mathcal{L}(f_\theta(x_i+\delta),y_i)\quad \mathrm{s.t.}\quad \|\delta\|_\infty \le \epsilon θmini=1∑NδmaxL(fθ(xi+δ),yi)s.t.∥δ∥∞≤ϵ其中 L \mathcal{L} L是图片分类器的交叉熵损失函数。由于找到内部最大化的最优解是非常困难的,对抗训练最常见的方法就是通过 P G D \mathrm{PGD} PGD来近似最坏情况下的对抗扰动。虽然这已经被证明可以产生鲁棒性模型,但是计算开销随着 P G D \mathrm{PGD} PGD迭代数量而线性增加。因此,当前的工作专注于通过一步逼近内部最大化最优解来降低对抗训练的成本。
假设损失函数对于输入的变化是局部线性的,那么可以知道对抗训练内部最大化具有封闭形式的解。 G o o d f e l l o w \mathrm{Goodfellow} Goodfellow利用这一点提出了 F G S M \mathrm{FGSM} FGSM,其中对抗扰动遵循梯度符号的方向, T r a m e r \mathrm{Tramer} Tramer等人建议在 F G S M \mathrm{FGSM} FGSM之前添加一个随机初始化。然而,这两种方法后来都被证明容易受到多步攻击,具体公式表示为 δ = ψ ( η + α ⋅ s i g n ( ∇ x i L ( f θ ( x i + η ) , y i ) ) ) \delta=\psi\left(\eta+\alpha \cdot \mathrm{sign}(\nabla_{x_i} \mathcal{L}(f_\theta(x_i+\eta),y_i))\right) δ=ψ(η+α⋅sign(∇xiL(fθ(xi+η),yi)))其中, η \eta η服从概率分布 Ω \Omega Ω。当 ψ \psi ψ是投影到 ℓ ∞ \ell_\infty ℓ∞操作,并且 Ω \Omega Ω是均匀分布 [ − ϵ , ϵ ] d [-\epsilon,\epsilon]^d [−ϵ,ϵ]d, d d d是输入空间的维数。
N - F G S M \mathrm{N\text{-}FGSM} N-FGSM对抗训练
在进行对抗性训练时,一种常见的做法是将训练期间使用的干扰限制在 ϵ - ℓ ∞ \epsilon \text{-}\ell_\infty ϵ-ℓ∞范围。其背后原理是,在训练期间增加扰动的幅度可能不必要地降低分类精度,因为在测试时不会评估约束球外的扰动。虽然通过剪裁或限制噪声大小来限制训练期间使用的扰动是一种常见做法,但是由于梯度剪切是在采取梯度上升步骤后执行的,所以剪切点可能不再进行有效的对抗训练。基于上述动机,作者主要探索梯度剪裁操作和随机步长中噪声的大小在单步方法中获得的鲁棒性的作用。作者本文中提出了一种简单有效的单步对抗训练方法 N - F G S M \mathrm{N\text{-}FGSM} N-FGSM,具体的计算公式如下所示: δ N - F G S M = η + α ⋅ s i g n ( ∇ x i L ( f θ ( x i + η ) ) , y i ) \delta_{\mathrm{N\text{-}FGSM}}=\eta+\alpha \cdot \mathrm{sign}(\nabla_{x_i}\mathcal{L}(f_\theta(x_i+\eta)),y_i) δN-FGSM=η+α⋅sign(∇xiL(fθ(xi+η)),yi)其中 η \eta η是从均分布 [ − k , k ] d [-k,k]^d [−k,k]d中采样得来。由于 N - F G S M \mathrm{N\text{-}FGSM} N-FGSM不涉及梯度剪裁,可以发它扰动的期望平方范数大于 R S - F G S M \mathrm{RS\text{-}FGSM} RS-FGSM。相关算法流程图,引理和定理的证明如下所示。

引理1(对抗扰动的期望): 已知 N - F G S M \mathrm{N}\text{-}\mathrm{FGSM} N-FGSM的对抗扰动如下定义: δ N - F G S M = η + α ⋅ s i g n ( ∇ x ℓ ( f ( x + η ) , y ) ) \delta_{\mathrm{N}\text{-}\mathrm{FGSM}}=\eta + \alpha\cdot \mathrm{sign}(\nabla_x \ell(f(x+\eta),y)) δN-FGSM=η+α⋅sign(∇xℓ(f(x+η),y))其中 η ∼ Ω \eta\sim \Omega η∼Ω,分布 Ω \Omega Ω是均匀分布 U ( [ − k ϵ , k ϵ ] d ) \mathcal{U}\left([-k\epsilon,k\epsilon]^d\right) U([−kϵ,kϵ]d),并且对抗扰动步长为 α > 0 \alpha > 0 α>0,则有 E [ ∥ δ N - F G S M ∥ 2 2 ] = d ( k 2 ϵ 2 3 + α 2 ) , E [ ∥ δ N - F G S M ∥ 2 ] ≤ d ( k 2 ϵ 2 3 + α 2 ) \mathbb{E}[\|\delta_{\mathrm{N\text{-}FGSM}}\|_2^2]=d\left(\frac{k^2\epsilon^2}{3}+\alpha^2\right),\quad \mathbb{E}[\|\delta_{\mathrm{N\text{-}FGSM}}\|_2]\le \sqrt{d\left(\frac{k^2\epsilon^2}{3}+\alpha^2\right)} E[∥δN-FGSM∥22]=d(3k2ϵ2+α2),E[∥δN-FGSM∥2]≤d(3k2ϵ2+α2)
证明: 由 J e n s e n \mathrm{Jensen} Jensen不等式可知,当时函数 f ( x ) = x f(x)=\sqrt{x} f(x)=x是凹函数,则有 E [ f ( x ) ] ≤ f ( E [ x ] ) \mathbb{E}[f(x)]\le f(\mathbb{E}[x]) E[f(x)]≤f(E[x])则以下不等式成立 E η [ ∥ δ N − F G S M ∥ 2 ] ≤ E η [ ∥ δ N - F G S M ∥ ] \mathbb{E}_\eta[\|\delta_{\mathrm{N-FGSM}}\|_2]\le \sqrt{\mathbb{E}_{\eta}[\|\delta_{\mathrm{N\text{-}FGSM}}\|]} Eη[∥δN−FGSM∥2]≤Eη[∥δN-FGSM∥]以下主要计算期望 E η [ ∥ δ N - F G S M ∥ ] \mathbb{E}_{\eta}[\|\delta_{\mathrm{N\text{-}FGSM}}\|] Eη[∥δN-FGSM∥]并将 ∇ x ℓ ( f ( x + η ) , y ) i \nabla_x \ell(f(x+\eta),y)_i ∇xℓ(f(x+η),y)i缩写为 ∇ ( η ) i \nabla(\eta)_i ∇(η)i,具体证明步骤如下所示 E η [ ∥ δ N − F G S M ∥ 2 2 ] = E η ∥ η + α ⋅ s i g n ( ∇ x ℓ ( f ( x + η ) , y ) ) ∥ 2 2 = E [ ∑ i = 1 d ( η i + α ⋅ s i g n ( ∇ ( η ) i ) ) 2 ] = ∑ i = 1 d E η [ ( η i + α ⋅ s i g n ( ∇ ( η ) i ) ) 2 ] = ∑ i = 1 d E η [ ( η i + α ⋅ s i g n ( ∇ ( η ) i ) ) 2 ∣ s i g n ( ∇ ( η ) i ) = 1 ] ⋅ P η [ s i g n ( ∇ ( η ) i ) = 1 ] + ∑ i = 1 d E η [ ( η i + α ⋅ s i g n ( ∇ ( η ) i ) ) 2 ∣ s i g n ( ∇ ( η ) i ) = − 1 ] ⋅ P η [ s i g n ( ∇ ( η ) i ) = − 1 ] = ∑ i = 1 d 1 2 k ϵ ∫ − k ϵ k ϵ ( η i + α ) 2 d η i ⋅ P η [ s i g n ( ∇ ( η ) i ) = 1 ] + 1 2 k ϵ ∑ i = 1 d ∫ − k ϵ k ϵ ( η i − α ) 2 d η i ⋅ P η [ s i g n ( ∇ ( η ) i ) = − 1 ] = ∑ i = 1 d 1 2 k ϵ ∫ α − k ϵ α + k ϵ z 2 d z ⋅ P η [ s i g n ( ∇ ( η ) i ) = 1 ] + ∑ i = 1 d 1 2 k ϵ ∫ − α − k ϵ − α + k ϵ z 2 d z ⋅ P η [ s i g n ( ∇ ( η ) i ) = − 1 ] = ∑ i = 1 d 1 2 k ϵ ∫ α − k ϵ α + k ϵ z 2 d z ⋅ P η [ s i g n ( ∇ ( η ) i ) = 1 ] + ∑ i = 1 d 1 2 k ϵ ∫ α − k ϵ α + k ϵ z 2 d z ⋅ P η [ s i g n ( ∇ ( η ) i ) = − 1 ] = 1 2 k ϵ ∫ α − k ϵ α + k ϵ z 2 d z ∑ i = 1 d ( P η [ s i g n ( ∇ ( η ) i ) = 1 ] + P η [ s i g n ( ∇ ( η ) i ) = − 1 ] ) = d 6 k ϵ [ ( α + k ϵ ) 3 − ( α − k ϵ ) 3 ] = d k 2 ϵ 2 3 + d α 2 \begin{aligned}\mathbb{E}_\eta[\|\delta_{\mathrm{N-FGSM}}\|^2_2]&=\mathbb{E}_\eta\|\eta+\alpha \cdot \mathrm{sign}(\nabla_x\ell(f(x+\eta),y))\|_2^2\\&=\mathbb{E}\left[\sum\limits_{i=1}^d(\eta_i+\alpha \cdot \mathrm{sign}(\nabla(\eta)_i))^2\right]\\&=\sum\limits_{i=1}^d \mathbb{E}_\eta[(\eta_i+\alpha \cdot \mathrm{sign}(\nabla(\eta)_i))^2]\\&=\sum\limits_{i=1}^d\mathbb{E}_\eta[(\eta_i + \alpha \cdot \mathrm{sign}(\nabla(\eta)_i))^2|\mathrm{sign}(\nabla(\eta)_i)=1]\cdot\mathbb{P}_\eta[\mathrm{sign}(\nabla (\eta)_i)=1]\\&+\sum\limits_{i=1}^d\mathbb{E}_\eta[(\eta_i + \alpha \cdot \mathrm{sign}(\nabla(\eta)_i))^2|\mathrm{sign}(\nabla(\eta)_i)=-1]\cdot\mathbb{P}_\eta[\mathrm{sign}(\nabla (\eta)_i)=-1]\\&=\sum\limits_{i=1}^d\frac{1}{2 k \epsilon} \int_{-k \epsilon}^{k\epsilon}(\eta_i+\alpha)^2 d\eta_i\cdot\mathbb{P}_\eta[\mathrm{sign}(\nabla(\eta)_i)=1]+\frac{1}{2 k \epsilon}\sum\limits_{i=1}^d\int_{-k\epsilon}^{k\epsilon}(\eta_i-\alpha)^2d\eta_i \cdot \mathbb{P}_\eta[\mathrm{sign}(\nabla(\eta)_i)=-1]\\&=\sum\limits_{i=1}^d\frac{1}{2 k\epsilon}\int_{\alpha-k\epsilon}^{\alpha+k\epsilon}z^2dz \cdot \mathbb{P}_\eta[\mathrm{sign}(\nabla(\eta)_i)=1]+\sum\limits_{i=1}^d\frac{1}{2 k\epsilon}\int_{-\alpha-k\epsilon}^{-\alpha+k\epsilon}z^2dz \cdot \mathbb{P}_\eta[\mathrm{sign}(\nabla(\eta)_i)=-1]\\&=\sum\limits_{i=1}^d\frac{1}{2 k\epsilon}\int_{\alpha-k\epsilon}^{\alpha+k\epsilon}z^2dz \cdot \mathbb{P}_\eta[\mathrm{sign}(\nabla(\eta)_i)=1]+\sum\limits_{i=1}^d\frac{1}{2 k\epsilon}\int_{\alpha-k\epsilon}^{\alpha+k\epsilon}z^2dz \cdot \mathbb{P}_\eta[\mathrm{sign}(\nabla(\eta)_i)=-1]\\&=\frac{1}{2k\epsilon}\int_{\alpha-k\epsilon}^{\alpha+k \epsilon}z^2 dz\sum\limits_{i=1}^d(\mathbb{P}_\eta[\mathrm{sign}(\nabla(\eta)_i)=1]+\mathbb{P}_\eta[\mathrm{sign}(\nabla (\eta)_i)=-1])\\&=\frac{d}{6 k \epsilon}[(\alpha+k \epsilon)^3-(\alpha-k \epsilon)^3]=\frac{d k^2 \epsilon^2}{3}+ d\alpha^2\end{aligned} Eη[∥δN−FGSM∥22]=Eη∥η+α⋅sign(∇xℓ(f(x+η),y))∥22=E[i=1∑d(ηi+α⋅sign(∇(η)i))2]=i=1∑dEη[(ηi+α⋅sign(∇(η)i))2]=i=1∑dEη[(ηi+α⋅sign(∇(η)i))2∣sign(∇(η)i)=1]⋅Pη[sign(∇(η)i)=1]+i=1∑dEη[(ηi+α⋅sign(∇(η)i))2∣sign(∇(η)i)=−1]⋅Pη[sign(∇(η)i)=−1]=i=1∑d2kϵ1∫−kϵkϵ(ηi+α)2dηi⋅Pη[sign(∇(η)i)=1]+2kϵ1i=1∑d∫−kϵkϵ(ηi−α)2dηi⋅Pη[sign(∇(η)i)=−1]=i=1∑d2kϵ1∫α−kϵα+kϵz2dz⋅Pη[sign(∇(η)i)=1]+i=1∑d2kϵ1∫−α−kϵ−α+kϵz2dz⋅Pη[sign(∇(η)i)=−1]=i=1∑d2kϵ1∫α−kϵα+kϵz2dz⋅Pη[sign(∇(η)i)=1]+i=1∑d2kϵ1∫α−kϵα+kϵz2dz⋅Pη[sign(∇(η)i)=−1]=2kϵ1∫α−kϵα+kϵz2dzi=1∑d(Pη[sign(∇(η)i)=1]+Pη[sign(∇(η)i)=−1])=6kϵd[(α+kϵ)3−(α−kϵ)3]=3dk2ϵ2+dα2进而则有 E η [ ∥ δ N - F G S M ∥ 2 ] ≤ d ( k 2 ϵ 2 3 + α 2 ) \mathbb{E}_\eta[\|\delta_{\mathrm{N\text{-}FGSM}}\|_2]\le\sqrt{d\left(\frac{k^2\epsilon^2}{3}+\alpha^2\right)} Eη[∥δN-FGSM∥2]≤d(3k2ϵ2+α2)证毕。
定理1: 令 δ N - F G S M \delta_{\mathrm{N\text{-}FGSM}} δN-FGSM是 N - F G S M \mathrm{N\text{-}FGSM} N-FGSM方法生成的对抗扰动, δ F G S M \delta_{\mathrm{FGSM}} δFGSM是 F G S M \mathrm{FGSM} FGSM方法生成的对抗扰动, δ R S - F G S M \delta_{\mathrm{RS\text{-}FGSM}} δRS-FGSM是 R S - F G S M \mathrm{RS\text{-}FGSM} RS-FGSM方法生成的对抗扰动,对于任意的 ϵ > 0 \epsilon>0 ϵ>0,则有以下不等式成立 E η [ ∥ δ N - F G S M ∥ 2 2 ] > E η [ ∥ δ F G S M ∥ 2 2 ] > E [ ∥ δ R S - F G S M ∥ 2 2 ] \mathbb{E}_{\eta}[\|\delta_{\mathrm{N\text{-}FGSM}}\|_2^2]>\mathbb{E}_\eta[\|\delta_{\mathrm{FGSM}}\|^2_2]>\mathbb{E}[\|\delta_{\mathrm{RS\text{-}FGSM}}\|^2_2] Eη[∥δN-FGSM∥22]>Eη[∥δFGSM∥22]>E[∥δRS-FGSM∥22]
证明:由引理1可知 E η [ ∥ δ N - F G S M ∥ 2 2 ] = d ( k 2 ϵ 2 3 + α 2 ) \mathbb{E}_\eta[\|\delta_{\mathrm{N\text{-}FGSM}}\|_2^2]=d\left(\frac{k^2\epsilon^2}{3}+\alpha^2\right) Eη[∥δN-FGSM∥22]=d(3k2ϵ2+α2)又因为 E η [ ∥ δ R S - F G S M ∥ 2 2 ] = d ( − 1 6 α 3 + 1 2 α 2 + 1 3 ϵ 2 ) \mathbb{E}_\eta[\|\delta_{\mathrm{RS\text{-}FGSM}}\|^2_2]=d\left(-\frac{1}{6}\alpha^3+\frac{1}{2}\alpha^2+\frac{1}{3}\epsilon^2\right) Eη[∥δRS-FGSM∥22]=d(−61α3+21α2+31ϵ2) E η [ ∥ δ F G S M ∥ 2 2 ] = ∥ δ F G S M ∥ 2 2 = d ϵ 2 \mathbb{E}_\eta[\|\delta_{\mathrm{FGSM}}\|_2^2]=\|\delta_{\mathrm{FGSM}}\|_2^2=d\epsilon^2 Eη[∥δFGSM∥22]=∥δFGSM∥22=dϵ2如果令超参数 k = 2 k=2 k=2, α = ϵ \alpha=\epsilon α=ϵ, α = 5 ϵ 4 \alpha=\frac{5\epsilon}{4} α=45ϵ,则有 E η [ ∥ δ N - F G S M ∥ 2 2 ] = 7 3 d ϵ 2 > E η [ ∥ δ F G S M ∥ 2 2 ] = d ϵ 2 > E η [ ∥ δ R S − F G S M ∥ 2 2 ] = 101 128 d ϵ 2 \mathbb{E}_\eta[\|\delta_{\mathrm{N\text{-}FGSM}}\|_2^2]=\frac{7}{3}d\epsilon^2>\mathbb{E}_\eta[\|\delta_{\mathrm{FGSM}}\|_2^2]=d \epsilon^2 > \mathbb{E}_\eta[\|\delta_{\mathrm{RS-FGSM}}\|_2^2]=\frac{101}{128}d \epsilon^2 Eη[∥δN-FGSM∥22]=37dϵ2>Eη[∥δFGSM∥22]=dϵ2>Eη[∥δRS−FGSM∥22]=128101dϵ2证毕。
实验结果
下图表示的是在数据集 C I F A R 10 \mathrm{CIFAR10} CIFAR10(左)和 S V H N \mathrm{SVHN} SVHN(右)上比较 N - F G S M \mathrm{N\text{-}FGSM} N-FGSM和 G r a d A l i g n \mathrm{GradAlign} GradAlign的多步方法在不同的扰动半径下使用神经网络 P r e a c t R e s N e t 18 \mathrm{PreactResNet18} PreactResNet18的分类准确率。可以发现尽管所有方法都达到干净样本的分类精度(虚线),但 P G D - 10 \mathrm{PGD\text{-}10} PGD-10和单步法之间在鲁棒精度方面存在差距,而且,最重要的是 P G D - 10 \mathrm{PGD\text{-}10} PGD-10是 N - F G S M \mathrm{N\text{-}FGSM} N-FGSM的计算开销的10倍。

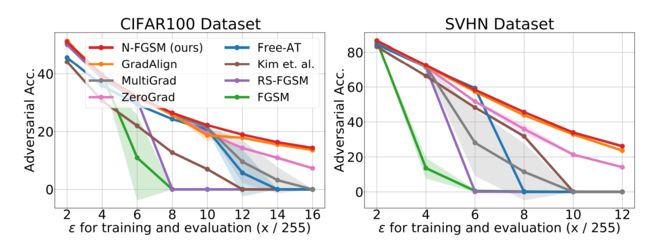
下图表示的是在数据在 C I F A R 100 \mathrm{CIFAR100} CIFAR100(左)和 S V H N \mathrm{SVHN} SVHN(右)上的单步方法与网络 P r e a c t R e s N e t 18 \mathrm{PreactResNet18} PreactResNet18在不同扰动半径上的比较。可以发现该论文的方法 N - F G S M \mathrm{N\text{-}FGSM} N-FGSM可以匹配或超过现有技术的结果,同时将计算成本降低3倍。
下图表示的是在训练开始(顶部)和结束(底部)的几个时期,对抗扰动 δ \delta δ和梯度平均值的可视化图。可以发现当过拟合之后, F G S M \mathrm{FGSM} FGSM和 R S - F G S M \mathrm{RS\text{-}FGSM} RS-FGSM无法对对抗扰动 δ \delta δ进行解释,其梯度也是如此,但是 N - F G S M \mathrm{N\text{-}FGSM} N-FGSM和 P G D - 10 \mathrm{PGD\text{-}10} PGD-10却可以避免这种情况的发生。

程序代码
该论文并没有提供源码,以下是在 m n i s t \mathrm{mnist} mnist数据集中对论文中代码进行的实现。
import argparse
import logging
import time
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision
from torchvision import datasets, transforms
from torch.utils.data import DataLoader, Dataset
import os
import argparse
def get_args():
parser = argparse.ArgumentParser()
parser.add_argument('--batch-size', default=100, type=int)
parser.add_argument('--data-dir', default='mnist-data', type=str)
parser.add_argument('--epochs', default=10, type=int)
parser.add_argument('--epsilon', default=0.3, type=float)
parser.add_argument('--alpha', default=0.375, type=float)
parser.add_argument('--lr-max', default=5e-3, type=float)
parser.add_argument('--lr-type', default='cyclic')
parser.add_argument('--fname', default='mnist_model', type=str)
parser.add_argument('--seed', default=0, type=int)
return parser.parse_args()
class Flatten(nn.Module):
def forward(self, x):
return x.view(x.size(0), -1)
def mnist_net():
model = nn.Sequential(
nn.Conv2d(1, 16, 4, stride=2, padding=1),
nn.ReLU(),
nn.Conv2d(16, 32, 4, stride=2, padding=1),
nn.ReLU(),
Flatten(),
nn.Linear(32*7*7,100),
nn.ReLU(),
nn.Linear(100, 10)
)
return model
class Attack_methods(object):
def __init__(self, model, X, Y, epsilon, alpha):
self.model = model
self.epsilon = epsilon
self.X = X
self.Y = Y
self.epsilon = epsilon
self.alpha = alpha
def nfgsm(self):
eta = torch.zeros_like(self.X).uniform_(-self.epsilon, self.epsilon)
delta = torch.zeros_like(self.X)
eta.requires_grad = True
output = self.model(self.X + eta)
loss = nn.CrossEntropyLoss()(output, self.Y)
loss.backward()
grad = eta.grad.detach()
delta.data = eta + self.alpha * torch.sign(grad)
return delta
class Adversarial_Trainings(object):
def __init__(self, epochs, train_loader, model, opt, epsilon, alpha, iter_num, lr_max, lr_schedule,
fname, logger):
self.epochs = epochs
self.train_loader = train_loader
self.model = model
self.opt = opt
self.epsilon = epsilon
self.alpha = alpha
self.iter_num = iter_num
self.lr_max = lr_max
self.lr_schedule = lr_schedule
self.fname = fname
self.logger = logger
def fast_training(self):
for epoch in range(self.epochs):
start_time = time.time()
train_loss = 0
train_acc = 0
train_n = 0
for i, (X, y) in enumerate(self.train_loader):
X, y = X.cuda(), y.cuda()
lr = self.lr_schedule(epoch + (i + 1) / len(self.train_loader))
self.opt.param_groups[0].update(lr=lr)
# Generating adversarial example
adversarial_attack = Attack_methods(self.model, X, y, self.epsilon, self.alpha)
delta = adversarial_attack.nfgsm()
# Update network parameters
output = self.model(torch.clamp(X + delta, 0, 1))
loss = nn.CrossEntropyLoss()(output, y)
self.opt.zero_grad()
loss.backward()
self.opt.step()
train_loss += loss.item() * y.size(0)
train_acc += (output.max(1)[1] == y).sum().item()
train_n += y.size(0)
train_time = time.time()
self.logger.info('%d \t %.1f \t %.4f \t %.4f \t %.4f', epoch, train_time - start_time, lr, train_loss/train_n, train_acc/train_n)
torch.save(self.model.state_dict(), self.fname)
logger = logging.getLogger(__name__)
logging.basicConfig(
format='[%(asctime)s] - %(message)s',
datefmt='%Y/%m/%d %H:%M:%S',
level=logging.DEBUG)
def main():
args = get_args()
logger.info(args)
np.random.seed(args.seed)
torch.manual_seed(args.seed)
torch.cuda.manual_seed(args.seed)
mnist_train = datasets.MNIST("mnist-data", train=True, download=True, transform=transforms.ToTensor())
train_loader = torch.utils.data.DataLoader(mnist_train, batch_size=args.batch_size, shuffle=True)
model = mnist_net().cuda()
model.train()
opt = torch.optim.Adam(model.parameters(), lr=args.lr_max)
if args.lr_type == 'cyclic':
lr_schedule = lambda t: np.interp([t], [0, args.epochs * 2 // 5, args.epochs], [0, args.lr_max, 0])[0]
elif args.lr_type == 'flat':
lr_schedule = lambda t: args.lr_max
else:
raise ValueError('Unknown lr_type')
logger.info('Epoch \t Time \t LR \t \t Train Loss \t Train Acc')
adversarial_training = Adversarial_Trainings(args.epochs, train_loader, model, opt, args.epsilon, args.alpha, 40,
args.lr_max, lr_schedule, args.fname, logger)
adversarial_training.fast_training()
if __name__ == "__main__":
main()
