【生信】基因组学中的统计学应用
【生信】基因组学中的统计学应用
本文图片来源网络或学术论文,文字部分来源网络与学术论文,仅供学习使用。
目录
【生信】基因组学中的统计学应用
1、生物统计学相关概念
2、统计学概念补充
统计描述和统计推断
数据(样本)的定义
数据(样本)的描述
数据的图表类描述
常见的分布
假设检验
单样本检验:汽车引擎排放实例
其他概念
3、基因组学统计应用
4、转录组学统计应用、
1、生物统计学相关概念
生物统计学:是生物数学中最早形成的一大分支,它是在用统计学的原理和方法研究生物学的客观现象及问题的过程中形成的,生物学中的问题又促使生物统计学中大部分基本方法进一步发展。
生物统计学的内容包括 试验设计 和 统计分析。
试验设计:指应用数理统计的原理与方法,制定试验方案,选择试验材料,合理分组,降低试验误差,使我们可以利用较少的人力、物力和时间,获得丰富而可靠的数据资料。
统计分析:指应用数理统计的原理与方法对数据资料进行分析与推断,认识客观事物的本质和规律性,使我们对所研究的资料得出合理的结论二由于事物都是相互联系的,统计不能孤立地研究各种现象,而必须通过一定数量的观察,从这些观察结果中研究事物问的相互关系。揭示出事物客观存在的规律性。
统计分析与试验设计是不可分割的两部分。试验设计须以统计分析的原理和方法为基础,而正确设计的试验又为统计分析提供了丰富、可靠的信息,两者紧密结合推断出合理的结论,不断地推动应用生物科学研究的发展。
2、统计学概念补充
统计描述和统计推断
数据的统计分析主要包括两部分:统计描述和统计推断。
统计描述:运用一些统计指标,如均值、标准差以及统计表和统计图等,对数据的数量特征及其分布规律进行客观地描述和表达,不涉及样本推断总体的问题。
统计推断:即在一定的置信度或概率保证下,根据样本信息去推断总体特征。通常包括参数估计和假设检验两个内容:
(1)参数估计:指用样本指标推断总体相应的指标。
例如根据部分城市人群的原发性高血压患病率去估计整个城市的原发性高血压患病率,参数估计又分为点估计和区间估计,比如:已知样本量为200、均数为100,标准差为5,对总体均数进行估计,如果直接用100作为总体的均数,这种估计方法被称为点估计,由于样本是随机的,抽出一个具体的样本得到的估计值很可能不同于总体真值。所以就有了另一种估计方法区间估计,它是在点估计的基础上,给出总体参数估计的一个区间范围,该区间通常由样本统计量加减估计误差得到。
(2)假设检验:指由样本之间的差异推断总体之间是否可能存在差异。
例如原发性高血压治疗药物在两组的疗效存在一定差别,假设检验回答这种差别是机会造成的,还是真实存在的。它又分为单尾检验和双尾检验,单尾是判断大于或者小于,双尾是判断是不是等于。举一个形象的例子:设总体均数为μ,如果用参数估计是:求μ=?而假设检验则是:判断μ=100?(双尾检验) u>100?(单尾检验)
数据(样本)的定义:
- 总体:包含研究的全部个体(数据)的集合
- 样本:从总体中抽出的一部分元素的集合,实际情况通常是我们很难拿到总体的数据,用样本来代替总体是一个不错的选择.
- 样本容量或样本量:构成样本的元素数目
- 有限总体:容量有限的总体;
- 无限总体:容量无限的总体,通常将容量非常大的有限总体也按无限总体处理。
- 参数:用来描述总体特征的概括性数字度量,这个概念有点抽象,比如总体标准差、总体平均数啊都是参数,由于总体数据通常是不知道的,所以参数也是一个未知数。因此我们需要进行抽样,根据样本估算总体参数。
- 统计量:用来描述样本特征的概括性数字度量,统计量是根据样本数据计算出来的一个量,他是样本的函数。通常我们所关心的样本统计量样本均数、样本标准差等。
数据(样本)的描述:
a)集中趋势描述:
- 众数:在统计分布上具有明显集中趋势点的数值,代表数据的一般水平,可用于定性数据和定量数据。
- 中位数:同样是一个描述中间位置的统计量,但是相比平均数,这个中间位置就是中位数,按照从大到小或者从小到大的顺序排列好,中间的位置就是中位数,如果有两位中位数那就相加之后除以2。如果一个数据的的分布中没有特别离谱的异常值,那么他们的中位数和平均数应该差不多。
- 平均数:描述数据中间位置的一个描述统计量,反应的是数据的集中趋势。但平均数容易受到异常值的影响,比如10个收入都为1万元的家庭和比尔盖茨比一下,那这组人群的的平均收入一定提高很多。
b)分散情况:
- 方差和标准差:衡量数据相对于平均值的分散程度,根据方差和标准差我们可以知道所观察的数据的分散情况。
- 变异系数:样本标准差除以均值,用变异系数可以比较不同样本相对变异程度的大小。
- 协方差:度量各个维度偏离其均值的程度。协方差的值如果为正值,则说明两者是正相关的,结果为负值就说明负相关的,如果为0,也是就是统计上说的“相互独立”。协方差仅能进行定性的分析。
c)分布形状:
- 偏度:偏度是统计数据分布偏斜方向和程度的度量,是统计数据分布非对称程度的数字特征,向左偏还是向右偏。偏度定义中包括正态分布(偏度=0),右偏分布(也叫正偏分布,其偏度>0),左偏分布(也叫负偏分布,其偏度<0)。
- 峰度:峰度又称峰态系数。表征概率密度分布曲线在平均值处峰值高低的特征数。直观看来,峰度反映了峰部的尖度。随机变量的峰度计算方法为:随机变量的四阶中心矩与方差平方的比值。峰度包括正态分布(峰度值=3),厚尾(峰度值>3),瘦尾(峰度值<3)。峰度越大,越高。
- 频数:指变量值中代表某种特征的数(标志值)出现的次数,如果在频数分布图中更胖的话表明你的数据越分散。
d)其他描述:
- 相关系数:相关系数是用以反映变量之间相关关系密切程度的统计指标。相关系数可以作定量的分析,看一看相关性到底有多大。
- 标准误:样本均数的标准差,是描述均数抽样分布的离散程度及衡量均数抽样误差大小的尺度,反映的是样本均数之间的变异。关于标准误这个概念很多人可能不了解,你想一下如果你只从总体中抽一次样本这样得到的均值和方差是否真的就能代表总体的均值或者方差呢?我们可不可以进行多次抽样,如果这样多次抽样后计算样本之间的标准差,标准差如果越小不就说明这些取样取的很好吗。
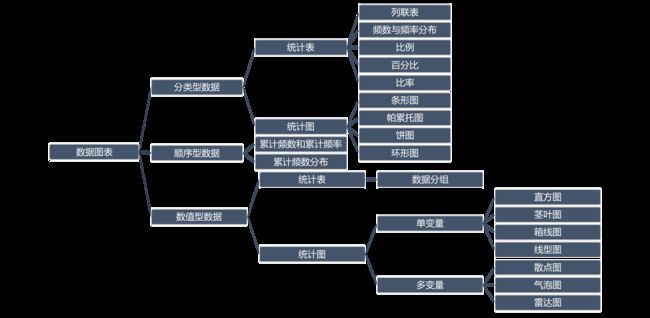
数据的图表类描述:
常见的分布:
正态分布:正态曲线呈钟型,两头低,中间高,左右对称因其曲线呈钟形,因此人们又经常称之为钟形曲线。在正态分布中我们通常认为在平均值左右三个标准差的范围内包含了大部分的数值。
二项分布:指的是重复n次独立的伯努利试验。在每次试验中只有两种可能的结果,而且两种结果发生与否互相对立,并且相互独立,与其它各次试验结果无关,事件发生与否的概率在每一次独立试验中都保持不变,则这一系列试验总称为n重伯努利实验,当试验次数为1时,二项分布服从0-1分布。
卡方分布:若n个相互独立的随机变量ξ₁,ξ₂,...,ξn ,均服从标准正态分布(也称独立同分布于标准正态分布),则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量,其分布规律称为卡方分布。
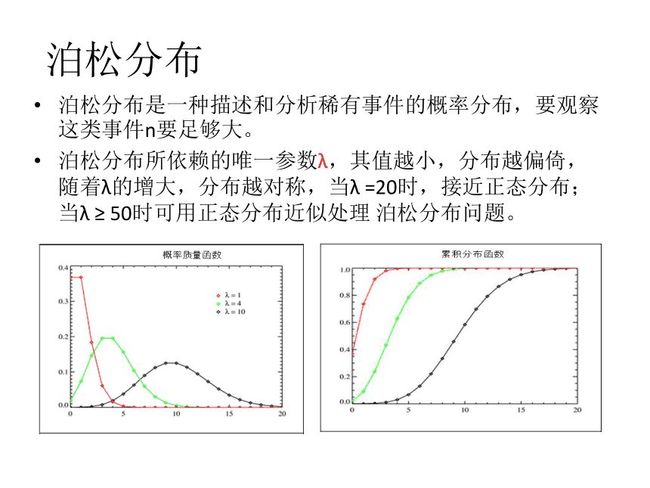
泊松分布:是一种描述和分析稀有事件的概率分布。要观察到这类事件,样本含量n必须很大。比如一个产品存在瑕疵的数量,广深高速每天出现交通事故的数量,放射性物质在单位时间内的放射次数,一匹布中疵点的数量等等。
指数分布:是一种连续概率分布。指数分布可以用来表示独立随机事件发生的时间间隔,比如旅客进机场的时间间隔、中文维基百科新条目出现的时间间隔等等。
几何分布:记每次试验中事件A发生的概率为p,试验进行到事件A出现时停止,此时所进行的试验次数为X,X的分布服从几何分布。
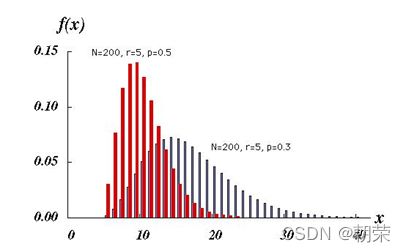
超几何分布:描述了从有限N个物件(其中包含M个指定种类的物件)中抽出n个物件,成功抽出该指定种类的物件的次数(不放回)。
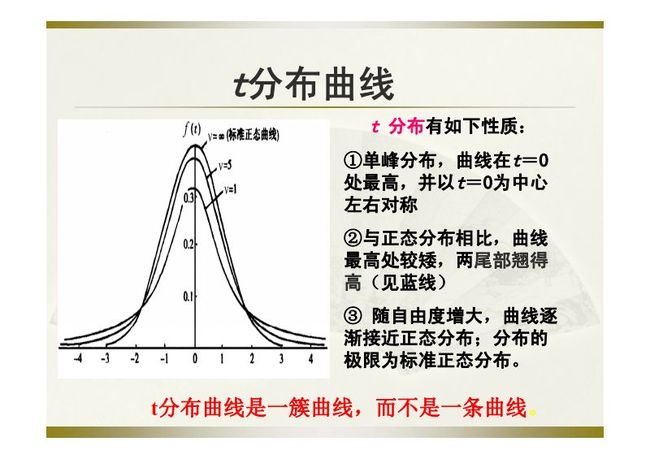
t分布:用于根据小样本来估计呈正态分布且方差未知的总体的均值。
假设检验
假设检验:假设检验一般分为四个步骤,提出假设-确定显著水平-计算概率-推断是否接受假设。假设检验首先要对总体做出假设,一般应作两个假设,一个是无效假设,一个是备择假设。无效意指要比较两个参数之间没有真实的差异,那么备择就是与之相反。两个假设是对立的。
- 原假设:根据检验结果准备予以拒绝或接受的假设,以H0表示;
- 备择假设:与原假设不相容(即对立)的假设,以H1表示
- 拒绝域:所使用的统计量可能取值的集合的某个子集合。如果根据观测值得出的统计量的数值属于这一集合,拒绝原假设;反之,接受原假设。
- 显著性水平:当原假设正确时,而被拒绝的概率的最大值,记为α。α的值一般取为0.05或0.01。
- 单尾/双尾假设检验:备择假设没有特定的方向性,称为双尾检测检验,单尾检测具有特定的方向性,并含有大于或者小于的假设检验。
- P值:P值是指在一个特定的统计模型下,从样本数据计算出的估计值(如两组间样本均数差)等于观测值或比观测值更为极端的概率
单样本检验:汽车引擎排放实例
汽车引擎新排放标准是平均值<20ppm,现某公司抽取10台汽车样本,其引擎排放水平为 15.6 16.2 22.5 20.5 16.4 19.4 16.6 17.9 12.7 13.9,判断该公司汽车是否符合新排放标准?
1、首先查看样本的描述统计信息,包括平均值,标准差等。
2、问题描述:判断该公司汽车引擎是否符合新排放标准
1)零假设:公司引擎排放不满足标准,即平均值>=20
备选假设:公司引擎排放满足标准,即平均值<20
2)检验类型
本案例是检验单个样本平均值是否等于目标值,所以是检验类型是单样本检验。
3)抽样分布类型
该样本n=10,不是正太分布,可将数据集可视化判断样本分布类型。从样本的数据集分布可看出,图形近似正态分布,样本量偏小,符合t分布。
4)检验方向
检验方向分为单尾和双尾,单尾又分为左尾和右尾。可通过备选假设的条件来判断。如果备选假设中包含“<”号,则为左尾检验,如果备选假设中包含“>”号,则为右尾检验,如果备选假设中包含“=”号,则为双尾检验。本案例备选假设中包含"<"号,则为左尾检验。
3、求出证据
即求出零假设成立时,得到样本平均值的概率p值。
计算t检验的统计量t值,将其和自由度df=n-1代入Statistical distributions and interpreting P values中可得双尾t检验的p值为0.0149,本案例左尾检验的p值为0.0149/2=0.00745。
其他概念
可参考笔记:【生信】统计学基础知识_朝荣的博客-CSDN博客
- 概率:研究不确定性事件和结果,比如2008年的金融危机,恰恰是华尔街预测模型中极小可能发生的事件同时发生了。用概率的语言来说就是概率很低的事件一起发生。因此所有的预测模型都是以概率为基础的。
- 变量:说明某种特征的概念,例如击球率,变量在上一次和下一次的测量是可以变化的,比如这一次击球率是40%,下一次是50%。具体可以分为分类变量(比如性别:男或者女)、顺序变量(奖项:一等奖、二等奖、三等奖)、数值型变量(年龄:1、2、3)。数值型根据取值的不同又可以分为离散型变量(比如年级)和连续型变量(比如温度)。
- 同质:根据研究目的所确定的观察单位其性质应大致相同。观察单位是研究的基本单元,可以是一个人、一个地点、一只动物、一份生物样品等。同质即为观察单位所受的影响相同。
- 变异:即使性质相同的事物,如果观察同一指标,各观察单位之间由于存在个体差异,也会使测量结果不同,这种差异称为变异。变异即为在观察单位在同质基础上的个体差异。例如,同种族、同年龄、同性别的健康人,在相同的条件下测其脉搏、呼吸、体温等生理指标均可能存在很大的差异。
- 四分位数:等于将数据分割为四等分的几个数值,最大的称为上四分位数,最小的称为下四分位数,中间的四分位数即中位数,上四分位数-下四分位数;常用全距量度数据常受异常值困扰,因此常关注位于数据中央的50%,排除异常值,这时用上了四分位数,用到四分位距。
- 中心极限定理:中心极限定理是概率论中讨论随机变量序列部分和分布渐近于正态分布的一类定理
- 大数定律:概率论中讨论随机变量序列的算术平均值向随机变量各数学期望的算术平均值收敛的定律。这个定理就是,在试验不变的条件下,重复试验多次,随机事件的频率近似于它的概率。比如一个均匀的骰子,你投掷的次数如果足够多,那么你得到的1-6的频率计算应该大致等于概率,就是每一个数字出现的概率为1/6方差分析。
- 方差分析:是通过对数据误差来源的分析来判断不同总体的均值是否相等,进而分析自变量(分类型)对因变量(数值型)是否有显著影响。可分为单因素方差分析,双因素方差分析。
3、基因组学统计应用
在测序过程中,通常需要回答这样一个问题:我们需要多少reads才能确保我们覆盖整个基因组?
回答这个问题,需要进行简单的假设,即测序所得的reads长度都是等长的,每条read均匀地分布在目标序列。然后我们给出如下定义:
G:以bp为单位,代表单倍体基因组的长度;
L:以bp为单位,随机测得的read的长度;
N:测序所得到的所有的read数目
c:read的覆盖深度 = NL/G
对于[0,G-1]中任何一个碱基位置x,他被某条read所覆盖的概率是L/G,由于测序项目中N条read独立均匀地分布在[0,G-1]上,因此该位置上的覆盖深度Nx,即覆盖它的read总数服从参数为n=N,p=L/G的二项分布。因为L<
由于G可以确定,L可以根据测序方案确定,所以我们可以通过确定 x至少为一条read覆盖的概率 来计算我们需要的reads数目。
4、转录组学统计应用、
检测基因表达水平
用于检测基因表达水平的 DNA 微阵列实验,应用之一是比较实验,目的是比较两个条件下的基因表达差异,从中识别出与条件相关的特异性基因,例如,识别可用于肿瘤分型的特异基因等。为了提高实验的可靠性,对于同一样本,往往有两次或更多次的重复实验,目的就是要识别在两个条件下有显著表达差异的基因。
何谓显著表达差异?
通常是指一个基因在两个条件中表达水平的检测值在排除实验、检测等因素外,达到一定的差异,具有统计学意义,同时也具有生物学意义。常用的分析方法有三类,第一类称之为倍数分析,计算每一个基因在两个条件下的 Ratio 值,若大于给定阈值,则为表达差异显著的基因;第二类方法采用统计分析中的 t 检验和方差分析,计算表达差异的置信度,来分析差异是否具有统计显著性;第三类是建模的方法,通过确定两个条件下的模型参数是否相同来判断表达差异的显著性,例如贝叶斯方法(这里不做介绍)。
倍数分析
早期基于 cDNA 微阵列技术的比较实验,用倍数来分析基因表达水平差异,即计算基因在两个条件下表达水平的比值。用 gi 表示基因 g 在条件 i 下的表达水平测量值,因此, 比值 g1/g2 可表示基因 g 在条件 1 和 2 下的表达水平差异。当 比值=1 时,基因 g 的表达水平没有改变,而 <1 或 >1 意味着基因 g 在两个条件下存在表达差异,特别是 <1 表示基因在条件 1 是下调的,而 >1 ,表示在条件 1 是上调的。在具体应用中,如果一个基因的平均表达水平在两个条件下的变化超过一个常数,典型的常数是 2 ,即 >2 或 <1/2 ,则认为该基因的表达差异是显著的。
然而,对表达数据仔细考察后可以发现,这样简单的 2 倍法并不能产生最优的结果,因为在不同的表达水平的基因上有相当不同的显著性。对于低表达水平的基因,其信噪比太低用 2 倍法作为判断条件太宽松(例如表达量从0.01上升到0.02很容易),而对于高表达基因,条件又太苛刻(例如表达量从1000上升到2000很困难),往往小于 2 就具有生物学意义。在具体应用中,并没有明确的阈值,往往根据分析的具体要求由数据分析者自行确定。
t 检验
于两个条件下的多次重复实验,为了判断基因的表达差异是否具有显著性,在应用中较多的是采用假设检验,包括两个条件下的 t 检验和多个条件下的方差分析( ANOVA ),这里仅仅介绍 t 检验,关于 ANOVA 请参考相应的统计分析书籍。
零假设为两个条件下的平均表达水平是相等的,备择假设为两个条件下的平均表达水平是不相等的。
定义:n为某一条件下的重复实验次数, Gij 是基因g在第i个条件下第j次重复实验的表达水平测量值。根据统计量值,可以得到 p 值,它表示在零假设成立的情况下,出现该数据的概率。如果 p 值小于给定的显著性水平,就拒绝零假设,即认为基因 g 在两个条件下的表达差异是显著的。因为在 t 检验中,两个总体平均值之间的距离被样本的标准差归一化,可以克服固定倍数阈值方法的一些缺点。然而,对于 DNA 微阵列数据的 t 检验的基本问题是,即使用当前的高通量检测技术,实验仍然花费很大或者实验过程很冗长,重复次数经常较小, 试验次数在2,3次的小样本仍然非常普通。由于样本量小,导致总体方差被严重低估,得到的 t 值就较大,因此会导致较高的假发现率,即通过 t 检验得到的结果中表达差异不显著的基因数目较多。这就需要对t值进行矫正,在这就不展开讲了,感兴趣的可以google一下(关键词:P值矫正)。