使用Matplotlib进行数据可视化(一)
前言
本篇为《使用Python进行数据分析》中介绍Matplotlib库的基础使用方法的第一篇,主要内容为使用Matplotlib库的一些常用技巧,绘画简易的线形图、散点图、密度图和等高线图等用图,以及进行可视化异常处理等。
Matplotlib是使用Python进行数据可视化的基本方法之一,操作简便快捷并且具有良好的操作系统兼容性和图形显示底层接口兼容性,对于数据分析新手来说,是非常好用的可视化工具。尽管近几年新的可视化工具在源源不断地进入大家的视野中,例如Seaborn、ggplot、HoloViews、AItair以及Pandas中对Matplotlib的API封装用法。但Matplotlib仍是可视化工具中的基础,并且掌握Matplotlib更能让你灵活地控制最终的图形结果,学习Matplotlib仍是学习可视化技术中不可或缺的一环。
目录
-
- 前言
- 1.Matplotlib常用技巧
-
- 1.1 导入Matplotlib
- 1.2 设置绘图样式
- 1.3 show() or not?
- 1.4 将图形保存为文件
- 2.两种绘图接口
- 3.绘制简易线形图
-
- 3.1 调整线条的颜色和风格
- 3.2 调整坐标轴
- 3.3 设置图形标签
- 4.绘制简易散点图
-
- 4.1 使用plt.plot画散点图
- 4.2 使用plt.scatter画散点图
- 4.3 plot与scatter的效率对比
- 5.饼图与条形图
-
- 5.1 条形图
- 5.2 饼图
- 6.密度图与等高线图
-
- 6.1 三维函数的可视化
- 7.频次直方图、数据区间划分与分布密度
-
- 7.1 频次直方图
- 7.2 二维频次直方图与数据区间划分
-
- 7.2.1 二维频次直方图`plt.hist2d()`
- 7.2.2 六边形区间划分`plt.hexbin()`
- 7.2.3 核密度估计(KDE方法)
- 8.可视化异常处理
-
- 8.1 基本误差线
- 8.2 连续误差
- 后记
1.Matplotlib常用技巧
1.1 导入Matplotlib
最常用的导入方式
import matplotlib as mpl
import matplotlib.pyplot as plt
1.2 设置绘图样式
在Matplotlib中可以使用plt.style来选择一种绘图风格,例如选择经典风格(classic),可以使用plt.style.available来查看可以使用的库中自带的风格,还可以自定义自己想要的绘图风格,有关绘图风格的详细使用方法会在后续介绍。
两种风格的对比
plt.style.use('classic')
x=np.linspace(0,10,100)
plt.plot(x,np.sin(x))
plt.style.use('bmh')
x=np.linspace(0,10,100)
plt.plot(x,np.sin(x))
1.3 show() or not?
在脚本文件中画图时,需要使用plt.show()来显示图形,需注意的是plt.show()通常需要放到脚本的最后,用来显示脚本的绘图。
但如果你使用IPython交互绘图,则不需使用show()命令。使用魔法命令%matplotlib启动Matplotlib模式后即可开始画图。
%matplotlib
Using matplotlib backend: TkAgg
import matplotlib.pyplot as plt
此后的任何plt命令都会自动打开一个图形窗口,增加新的命令就会使图形更新。对于不会即时更新的命令可以使用plt.draw()强制更新。
1.4 将图形保存为文件
我们可以使用plt.savefig()命令将绘制的图形保存为文件,且可以指定图片的分辨率、边缘的颜色等参数,具体的使用方法可以参考这篇博文:Python中Matplotlib Savefig()不同参数的使用.
2.两种绘图接口
能够分辨Matplotlib的两种绘图接口是非常重要的。初学者经常会搞混或弄不清楚这是怎么回事,接下来介绍这两种绘图接口:一个是便捷的MATLAB风格接口,另一个是功能更强大的面向对象接口。
#MATLAB接口
x=np.linspace(1,10,100)
plt.figure() #创建图形
#创建两个子图中的第一个,设置坐标轴
plt.subplot(2,1,1) #行,列,子图编号
plt.plot(x,np.sin(x))
#创建两个子图中的第二个,设置坐标轴
plt.subplot(2,1,2)
plt.plot(x,np.cos(x))
plt.rcParams['figure.figsize']=(5.0,3.0)
#面向对象接口
#先创建图形网格
#ax是一个包含两个Axes对象的数组
fig,ax=plt.subplots(2)
#在每个对象上调用plot()方法
ax[0].plot(x,np.sin(x))
ax[1].plot(x,np.cos(x))
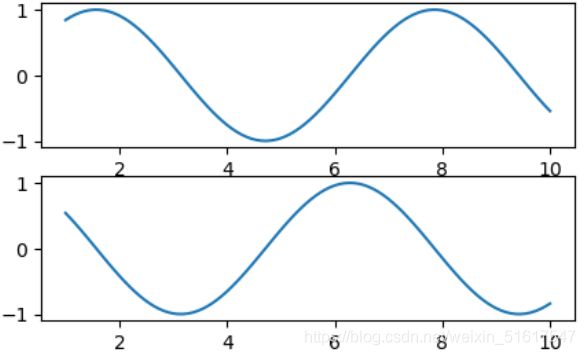
MATLAB接口对于初学者来说使用起来会更清楚,更方便而且更快捷。而面向对象的接口则可以适应更复杂的场景,更好地控制你自己的图形。随着后续更深层次内容的介绍,大家会更加了解两种接口的使用以及它们之间的区别和联系。
3.绘制简易线形图
现在,让我们来创建一个简单的线形图,即实现线性方程 y = f ( x ) y=f(x) y=f(x)的可视化。
首先,创建一个图形fig和一个坐标轴ax。
plt.style.use('bmh') #根据自己的喜好设置绘图风格
fig=plt.figure()
ax=plt.axes()
结果如下

在Matplotlib中,figure相当于创建了一张空白的画布,可以容纳各种坐标轴、图形、文字和标签;而axes则是一个带有刻度和标签的矩形,最终会包含所有可视化的图形元素。在创建好坐标轴后,就可以用ax.plot来画图了。
fig=plt.figure()
ax=plt.axes()
x=np.linspace(0,10,1000)
ax.plot(x,np.sin(x))
plt.plot(x,np.sin(x)) #直接使用plot命令,不使用面向对象的接口
plt.plot(x,np.cos(x))
3.1 调整线条的颜色和风格
首先介绍plot函数中可以进行调整的参数plt.plot(x,y,color,linestyle,marker,alpha,linewidth,markersize)
| x,y | 表示x轴和y轴所对应的数据 |
|---|---|
| color | 指定线条的颜色 |
| linestyle | 指定线条类型 |
| marker | 表示绘制的点的类型 |
| alpha | 表示点的透明度,用0-1之间的小数表示 |
| linewidth | 表示线条的宽度,取0-10之间的数值 |
| markersize | 点的大小 |
接下来介绍几种常用参数的常用取值
color参数常用的八种取值(颜色)的缩写
| 颜色缩写 | 代表的颜色 | 颜色缩写 | 代表的颜色 |
|---|---|---|---|
| b | 蓝色 | g | 绿色 |
| y | 黄色 | m | 品红 |
| k | 黑色 | w | 白色 |
| r | 红色 | c | 青色 |
linestyle常用取值
| linestyle取值 | 线条风格 | linestyle取值 | 线条风格 |
|---|---|---|---|
| - | 实线 | -. | 点线 |
| - - | 长虚线 | : | 短虚线 |
线条标记解释
| marker取值 | 点的类型 | marker取值 | 点的类型 |
|---|---|---|---|
| ‘o’ | 圆圈 | ‘.’ | 点 |
| ‘D’ | 菱形 | ‘s’ | 正方形 |
| ‘h’ | 六边形1 | ‘H’ | 六边形2 |
| ‘d’ | 小菱形 | ‘-’ | 水平线 |
| ‘v’ | 一角朝下的三角形 | ‘8’ | 八边形 |
| ‘<’ | 一角朝左的三角形 | ‘p’ | 五边形 |
| ‘>’ | 一角朝右的三角形 | ‘,’ | 像素 |
| ‘^’ | 一角朝上的三角形 | ‘+’ | 加号 |
| ‘\’ | 竖线 | ‘*’ | 星号 |
| ‘x’ | 叉号(X) | ‘None’ | 无 |
现在举实例说明其具体使用方法
plt.plot(x,np.sin(x),color='blue') #标准颜色名称
plt.plot(x,np.sin(x),color='g') #缩写颜色代码(rgbcmyk)
plt.plot(x,np.sin(x),color='0.75') #范围在0~1之间的灰度值
plt.plot(x,np.sin(x),color='#FFDD44') #十六进制(RRGGBB,00~FF)
plt.plot(x,np.sin(x),color=(1.0,0.2,0.3)) #RGB元组,范围在0~1
plt.plot(x,np.sin(x),color='chartreuse') #HTML颜色名称
plt.plot(x,np.sin(x),linestyle='-') #实线
plt.plot(x,np.sin(x),linestyle='--') #长虚线
plt.plot(x,np.sin(x),linestyle='-.') #点线
plt.plot(x,np.sin(x),linestyle=':') #短虚线
也可以将linestyle和color参数组合起来,用更简洁的表示方式绘图
plt.plot(x,x+1,'-g')
plt.plot(x,x+2,'--c')
plt.plot(x,x+3,'-.k')
plt.plot(x,x+4,':r')
3.2 调整坐标轴
虽然Matplotlib会为你自动生成坐标轴,但自定义的坐标轴会更符合我们的需求。其最基本的方法是使用plt.xlim()与plt.ylim()来调整坐标轴的上下限。
plt.plot(x,np.sin(x))
plt.xlim(-1,11)
plt.ylim(-1.5,1.5)
plt.plot(x,np.sin(x))
plt.xlim(10,0)
plt.ylim(1.5,-1.5)
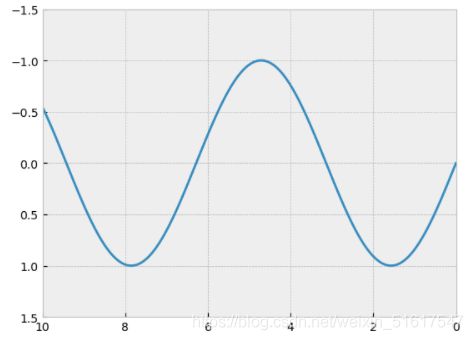
再介绍plt.axis()方法,这是一种对坐标轴进行设置的常用方法,例如:
设置坐标轴的上下限plt.axis([-x,x,-y,y])
令图形内容自动紧缩,不留空隙plt.axis('tight)
让x轴与y轴的单位长度相等plt.axis('equal')
开、关坐标轴plt.axis('on'\'off')
等等功能,更详细的使用方法可以查询官网或浏览其他博文,如matplotlib系列-plt.axis
plt.plot(x,np.sin(x))
plt.axis([-1,11,-1.5,1.5])
plt.axis('equal')
plt.axis('off')
3.3 设置图形标签
本节简要介绍设置图形标签的方法:图形标题、坐标轴标题、简易图例。
其中图形标题和坐标轴标题是最简单的标签,快速设置方法如下:
plt.plot(x,np.sin(x))
plt.title('A Sine Curve') #设置图形标题
plt.xlabel('x') #设置x轴标题
plt.ylabel('sin(x)') #设置y轴标题

我们可以通过调整参数来调整它们的位置,大小和风格。例如size(改变字体大小)、weight(调整字体粗细)和rotation(调整角度),在此不作过多介绍。
例如
plt.plot(x,np.sin(x))
plt.title('A Sine Curve')
plt.xlabel('x',size=50)
plt.ylabel('sin(x)',rotation=0)
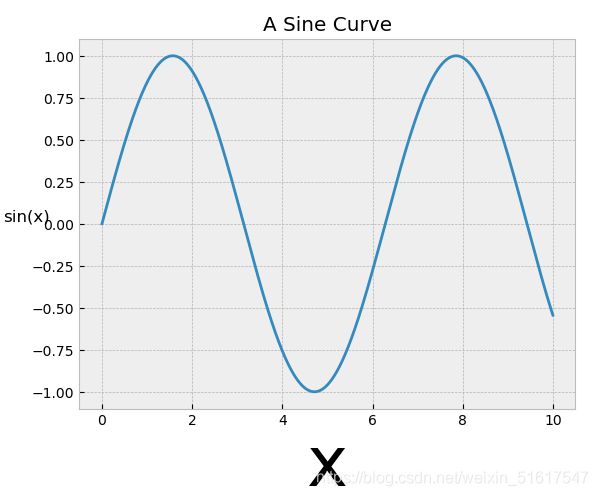
在单个坐标轴上同时显示多条线时,创建图例显示每条线是很有效的方法。Matplotlib内置了一个可以用来简单快速创建图例的方法,那就是plt.legend()。
plt.plot(x,np.sin(x),'-b',label='sin(x)')
plt.plot(x,np.cos(x),':r',label='cos(x)')
plt.axis('equal')
plt.legend()
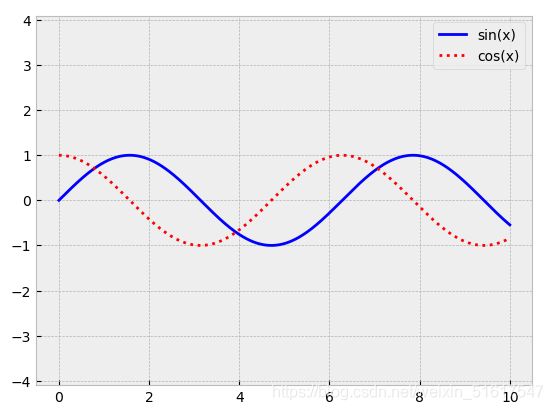
在此不再对plt.legend()函数做过多的介绍,在之后的内容中还会介绍更多高级的图例设置方法。
4.绘制简易散点图
另一种常用的图形是散点图(scatter plot),它与线形图类似,只不过不再由线段连接,而是由独立的点、圆圈或是其他形状构成。
4.1 使用plt.plot画散点图
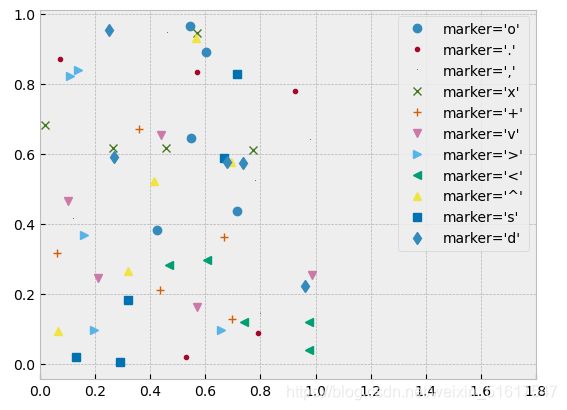
与绘制线形图一样,绘制散点图时也可以通过调整参数来自定义绘制的效果,比如颜色和点的形状,用代码示例具体的效果
plt.plot(x,y,marker,color)
rng=np.random.RandomState(0)
for marker in['o','.',',','x','+','v','>','<','^','s','d']:
plt.plot(rng.rand(5),rng.rand(5),marker,label="marker='{0}'".format(marker))
plt.legend(numpoints=1)
plt.xlim(0,1.8)
plt.plot(x,y,'-*',color='blue',markersize=15,linewidth=3,markerfacecolor='pink',markeredgecolor='blue',markeredgewidth=2)
plt.ylim(-1.2,1.2)
4.2 使用plt.scatter画散点图
plt.scatter的功能非常强大,它与plt.plot的差别在于它具有更高的灵活性,可以单独控制每个散点与数据匹配,也可以让每个散点具有不同的属性(大小、颜色等)。
plt.scatter(x,y,s,c,marker,alpha)
| 参数名称 | 说明 |
|---|---|
| x,y | 表示坐标轴上的数据 |
| s | 指定点的大小,接收单个值或一维的array数组 |
| c | 制定点的颜色,接收单个值或一维的array数组 |
| marker | 表示绘制点的类型 |
| alpha | 表示点的透明度,范围0-1 |
plt.style.use('default') #使用原始风格
rng=np.random.RandomState(0)
x=rng.randn(100)
y=rng.randn(100)
colors=rng.rand(100)
sizes=1000*rng.rand(100)
plt.scatter(x,y,c=colors,s=sizes,alpha=0.3,cmap='viridis')
plt.colorbar() #显示颜色条
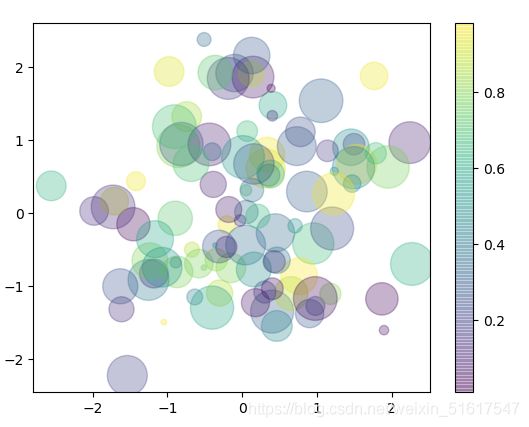
散点的颜色和大小可以显示多维数据的信息。让我们举一实例,使用Scikit-Learn程序库中的鸢尾花(iris)数据集来演示。它里面有三种鸢尾花,每个样本是一种花,其花瓣(petal)与花萼(sepal)的长度和宽度都经过了仔细测量。
from sklearn.datasets import load_iris
iris=load_iris()
features=iris.data.T
plt.scatter(features[0],features[1],alpha=0.2,s=100*features[3],c=iris.target,cmap='viridis')
plt.xlabel(iris.feature_names[0])
plt.ylabel(iris.feature_names[1])

由此我们可以看出,散点图可以同时看到不同维度的数据:每个点的坐标值(x,y)分别表示花萼的长度和宽度,而点的大小表示花瓣的宽度,三种颜色对应三种不同类型的鸢尾花。这类多颜色与多特征的散点图在探索与演示数据时非常有用。
4.3 plot与scatter的效率对比
由于plt.scatter会对每个散点进行单独的大小和颜色的渲染,因此渲染器会消耗更多的资源。而在plt.plot中,散点基本都彼此复制,因此整个数据集中所有点的颜色、大小都只需要配置一次。因此,在处理大型数据集时它们之间的效率和性能差异就很大了,在面对大型数据集时,plt.plot是更好的方法。当然,例如通过抽样对大型数据集进行处理缩小规模等,就是另外的事情了。
5.饼图与条形图
5.1 条形图
绘制条形图或说柱状图,我们使用plt.bar()函数,其常用参数表如下
plt.bar(left,height,width=0.8,color)
| 参数名称 | 说明 |
|---|---|
| left | 表示x轴的数据 |
| height | 表示x轴数据的数量 |
| width | 表示条形图的宽度,范围0-1,默认为0.8 |
| color | 表示条形图的颜色 |
x=np.linspace(0,10,10)
plt.bar(x,np.sin(x))
x=np.linspace(0,10,30)
plt.bar(x,np.sin(x),color=['red','blue','green'])
若想绘制横向的柱状图,则需使用plt.barh()函数,用法与bar函数相同。
x=np.linspace(0,10,10)
plt.barh(x,np.sin(x))
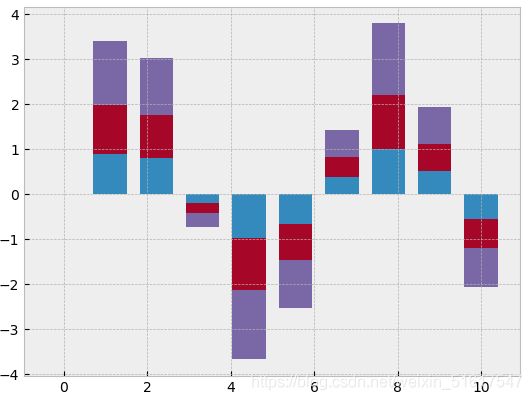
我们可以通过使用bottom参数来实现柱状图的堆叠
x=np.linspace(0,10,10)
plt.bar(x,np.sin(x))
plt.bar(x,1.2*np.sin(x),bottom=np.sin(x))
plt.bar(x,1.6*np.sin(x),bottom=np.sin(x)+1.2*np.sin(x))
plt.style.use('bmh')
x=np.linspace(0,10,10)
plt.bar(x,np.sin(x),width=0.3)
plt.bar(x+0.3,1.2*np.sin(x),width=0.3)

本文在此只对几种简单的绘制方法做介绍,了解更多方法可查询官网或参考其他博文。
5.2 饼图
绘制饼图,我们使用plt.pie()函数,其常用参数表如下
plt.pie(x,explode,labels,colors,autopct,pctdistance=0.6,labeldistance=1.1,radius)
| 参数名称 | 说明 | 参数名称 | 说明 |
|---|---|---|---|
| x | 表示用于绘制饼图的数据 | explode | 表示指定项离饼图圆心为n个半径 |
| labels | 指定每一项的名称 | colors | 表示饼图颜色 |
| autopct | 指定数值精度,数据会自动换算成百分比 | pctdistance | 指定每一项的比例和距离饼图圆心n个半径 |
| labeldistance | 指定每一项的名称和距离饼图圆心n个半径 | radius | 表示饼图的半径 |
| shadow | bool类型,给饼图加上阴影,默认为False | startangle | 设置起始角度 |
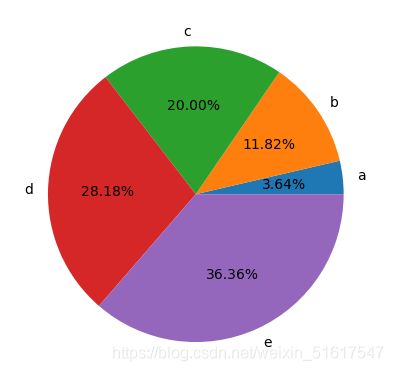
x=np.linspace(1,10,5)
plt.pie(x,labels=['a','b','c','d','e'],autopct="%1.2f%%",radius=1)
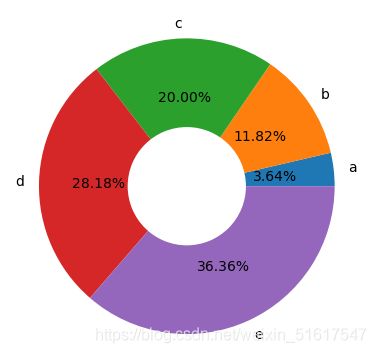
如果要创建环形饼图,在创建饼图后再创建一个纯白色的半径更小的饼图即可。
x=np.linspace(1,10,5)
plt.pie(x,labels=['a','b','c','d','e'],autopct="%1.2f%%",radius=1)
plt.pie([1],colors='w',radius=0.4)
了解更多创建饼图的方法可查询官网和参考其他博文。
6.密度图与等高线图
有时在二维图上用等高线图或色彩图来表示三维数据是不错的方法。Matplotlib提供了三个函数来解决这个问题:用plt.contour()画等高线图、用plt.contourf()画带有填充色的等高线图(filled contour plot)的色彩、用plt.imshow()显示图形。
6.1 三维函数的可视化
用函数 z = f ( x , y ) z=f(x,y) z=f(x,y)演示等高线图,按照下面的方式生成函数:
def f(x,y):
return np.sin(x)**10+np.cos(10+y*x)*np.cos(x)
等高线图可以用plt.contour()函数来创建。它需要三个参数:x轴,y轴和z轴三个坐标轴的网格数据。x轴与y轴表示图形中的位置,而z轴将通过等高线的等级来表示。使用np.meshgrid()函数来准备这些数据是一个比较简单的方法,它可以从一维数组构建二维网格数据:
x=np.linspace(0,5,50)
y=np.linspace(0,5,40)
X,Y=np.meshgrid(x,y)
Z=f(X,Y)
下面我们来创建等高线图:
plt.contour(X,Y,Z,6)

其中,6表示将数据范围等分为6份。此外,我们可以通过使用colors参数与cmap参数来设置等高线图的颜色,特别需要注意的是,在只使用一种颜色时,默认使用虚线表示负数,使用实线表示正数。
接下来,我们使用plt.contourf()来创建填充的等高线图,它的语法与plt.contour()是一样的。另外我们可以使用plt.colorbar()来创建一个表示图形各种颜色对应标签信息的颜色条。
plt.contourf(X,Y,Z,6)
plt.colorbar()
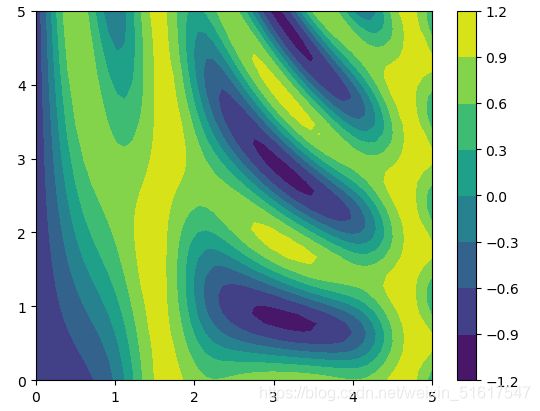
通过颜色条,我们可以清晰地看出,黄色的部分对应的数值最高,是“波峰(peak)”;深蓝色的部分对应的数值最低,是“波谷(valley)”。
我们还可以通过plt.imshow()函数来将二维数组渲染成渐变图。
plt.imshow(Z,extent=[0,5,0,5],origin='lower')
plt.colorbar()

使用plt.imshow()需要注意以下几点:1.它不支持用x轴和y轴数据设置网格,而是必须通过extent参数设置图形的坐标范围[xmin,xmax,ymin,ymax]。2.默认使用标准的图形数组定义,即原点位于左上角,这一点在显示网格数据图形时必须调整。3.plt.imshow()会自动调整坐标轴的精度以适应数据显示。可以通过plt.axis(aspect='image')来设置x轴与y轴的单位。
另外,再介绍一种方法,将等高线图与彩色图组合起来。
contours=plt.contour(X,Y,Z,3,colors='black')
plt.clabel(contours,inline=True,fontsize=8) #在等高线图中加入label
plt.imshow(Z,extent=[0,5,0,5],origin='lower',alpha=0.5)
plt.colorbar()

基于这几种方式,使用二维图表示三维数据的方法就有很多种可能了,想要了解更多的读者可以查询官网或是参考其他博文。
7.频次直方图、数据区间划分与分布密度
7.1 频次直方图
直接引入实例来讲解
x1=np.random.normal(0,0.8,1000)
x2=np.random.normal(-2,1,1000)
x3=np.random.normal(3,2,1000)
kwargs=dict(histtype='stepfilled',alpha=0.3,density=True,bins=40,edgecolor='none')
plt.hist(x1,**kwargs)
plt.hist(x2,**kwargs)
plt.hist(x3,**kwargs)
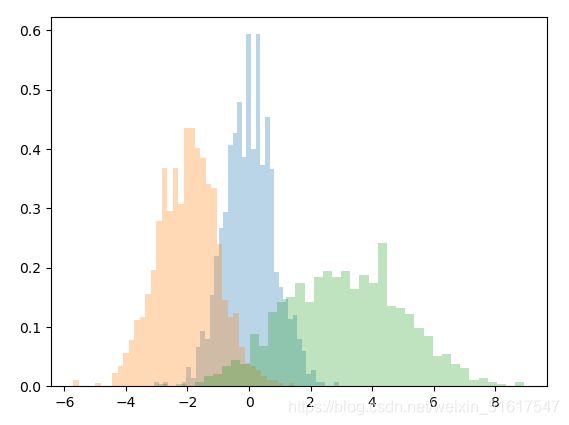
如上例所示,使用这样的直方图可以很好地帮助我们分析数据的分布情况,并对不同数据集的分布特征进行对比。现简要介绍用到的几个参数。
histtype是使用直方图的类型,常用类型有:‘bar’,‘barstacked’,‘step’,‘stepfilled’。
alpha指的是绘制直方图的透明度。
density是bool类型,若其值为True,则将频数转化为频率绘制直方图,即将频数归一化。
bins是指直方图柱形的数量,即区间内的分组个数。
edgecolor即是边缘颜色。
常用的其他参数还有’color’(直方图颜色),‘bottom’(y轴的起始位置),‘orientation’(直方图显示方式horizontal or vertical)等,具体方法可查询官网或参考其他博文。例如:【Matplotlib】(五)直方图(频数统计图).
另外,提供仅计算出每段区间样本数的代码:
counts,bin_edges=np.histogram(x1,bins=20)
print(counts)
7.2 二维频次直方图与数据区间划分
就像将一维数组分为区间创建一维频次直方图一样,我们也可以将二维数组按照二维区间进行切分,来创建二维频次直方图。下面来简单介绍几种创建二维频次直方图的方法。
7.2.1 二维频次直方图plt.hist2d()
mean=[0,0]
cov=[[1,1],[1,2]]
x,y=np.random.multivariate_normal(mean,cov,10000).T
plt.hist2d(x,y,bins=30)
plt.colorbar()
另外,二维频次直方图也可以提供仅计算出每段区间样本数的代码:
counts,xedges,yedges=np.histogram2d(x,y,bins=20)
print(counts)
7.2.2 六边形区间划分plt.hexbin()
二维频次直方图是正方形分割的,还有一种常用的方式是用正六边形分割。
plt.hexbin(x,y,gridsize=30)
plt.colorbar()
plt.xlim(-3.5,3.5)
plt.ylim(-4.5,4.5)
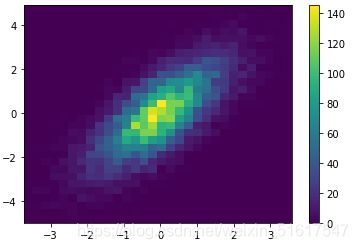
7.2.3 核密度估计(KDE方法)
KDE方法是一种评估多维数据分布密度的常用方法,在scipy.stats中有一个简单快速实现KDE的方法,现在来举例演示:
from scipy.stats import gaussian_kde
#拟合数组维度[Ndim,Nsamples]
data=np.vstack([x,y])
kde=gaussian_kde(data)
#用一对规则的网格数据进行拟合
xgrid=np.linspace(-3.5,3.5,40)
ygrid=np.linspace(-6,6,40)
Xgrid,Ygrid=np.meshgrid(xgrid,ygrid)
Z=kde.evaluate(np.vstack([Xgrid.ravel(),Ygrid.ravel()]))
#画出结果图
plt.imshow(Z.reshape(Xgrid.shape),origin='lower',aspect='auto',extent=[-3.5,3.5,-6,6])
plt.colorbar()

用Matplotlib做KDE的可视化图的过程比较繁琐,之后会介绍的Seaborn库中会提供更简洁的方法。
8.可视化异常处理
误差在测量过程中是不可避免的,如果仅有对测量数据的可视化,那么就无法直观的展示数据的可信程度或说难以直观的感受到与理论值的差异。在数据可视化的结果中用图形展示误差,就可以提供更充分的信息。
8.1 基本误差线
x=np.linspace(0,10,50)
dy=0.8
y=np.sin(x)+dy*np.random.randn(50)
plt.errorbar(x,y,yerr=dy,fmt='o',color='k',ecolor='lightblue',elinewidth=3,capsize=0)
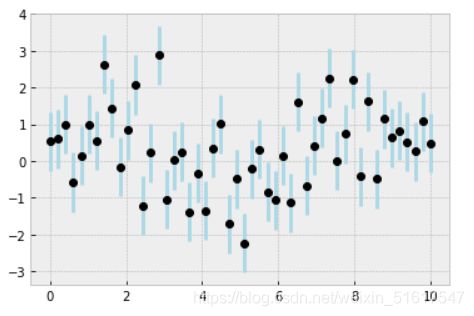
在此仅介绍简单的绘制方法,更多选项和参数的信息可参考plt.errorbar()的程序文档。
8.2 连续误差
有时我们需要显示连续变量的误差。Matplotlib中并没有内置的简便方法可以解决这个问题,但是通过plt.fill_between()来解决也不是难题。
在这里,我们仅展示一个例子:
注:以下代码参考博文【Python实例第36讲】一个高斯过程回归的例子.
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, ConstantKernel as C
def f(x):
return x * np.sin(x)
kernel = C(1.0, (1e-3, 1e3)) * RBF(10, (1e-2, 1e2))
gp=GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=9)
X = np.atleast_2d([1., 3., 5., 6., 8.]).T
y = f(X).ravel()
x = np.atleast_2d(np.linspace(0, 10, 1000)).T
gp.fit(X, y)
y_pred, sigma = gp.predict(x, return_std=True)
plt.figure()
plt.plot(X, y, 'r.', markersize=10, label=u'Observations')
plt.plot(x, y_pred, 'b-', label=u'Prediction')
plt.fill(np.concatenate([x, x[::-1]]),
np.concatenate([y_pred - 1.9600 * sigma,
(y_pred + 1.9600 * sigma)[::-1]]),
fc='lightblue', ec='None', label='95% confidence interval')
plt.xlabel('$x$')
plt.ylabel('$f(x)$')
plt.ylim(-10, 20)
plt.legend(loc='upper left')
我们使用了高斯过程回归方法,从图中可以看出,在接近观测点的位置,模型受到强约束,拟合误差很小,非常接近真实值;而在远离样本的区域,模型不受约束,误差不断增大。
后续我们会介绍Seaborn库中实现连续误差线的简便方法。
后记
以上便是《使用Matplotlib进行数据可视化(一)》的全部内容了,这算是笔者自己的学习记录,也算是个人经验的一些分享,我会不定期更新这一系列的内容,希望能够给各位读者带来一定的帮助。