Leetcode 【495、835】

问题描述：【Array】495. Teemo Attacking

解题思路：

读完题目，很容易想到要比较相邻两次攻击时间与中毒持续时间的关系：

• 如果相邻两次攻击时间的间隔大于等于中毒持续时间，总中毒时间就要累加一个完整的中毒持续时间；
• 如果相邻两次攻击时间的间隔小于中毒持续时间，那么艾希中毒还没结束就又中了一次毒，这样总中毒时间只需要累加这个间隔即可。

Python3 实现：

class Solution:
    def findPoisonedDuration(self, timeSeries: List[int], duration: int) -> int:
        if timeSeries == []:
            return 0
        time = duration
        for i in range(1, len(timeSeries)):
            if timeSeries[i] - timeSeries[i-1] >= duration:
                time += duration
            else:
                time += (timeSeries[i] - timeSeries[i-1])
        return time

---

问题描述：【Array】835. Image Overlap

解题思路：

方法1（时间复杂度 O(n^4)，空间复杂度 O(1)）：

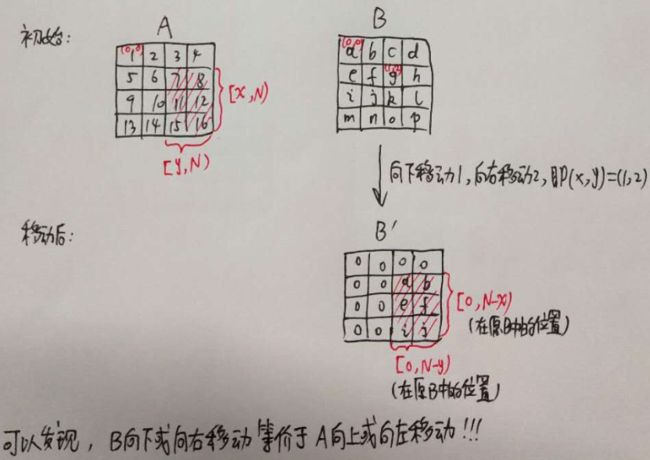
抛开移动的过程只看移动完成的结果。记图片左上角为顶点 (0, 0)，正方形边长为 N，要使得两张图片有重叠，那么其中一张图片移到的某一点 (x, y) 一定与另外一张图片的顶点 (0, 0) 重合。

假设移动图片 A，使其与图片 B 的顶点 (0, 0) 重合。设图片 A 移动到点 (x, y) 得到 A'，那么 A 与 B 重叠的区域就是 A：（[0, N-x)，[0, N-y)），B：（[x, N), [y, N)） 。例如，A 最终移动到 (x=1, y=2)，重叠区域如下图所示：

因此，我们只需要计算 A 与 B 的重叠部分中每个点都为 1 的个数，就是 A 移动到 (x, y) 与 B (0,0) 重叠时候能得到的 overlap。

注意：这样做我们的图片 A 是向右或者向下移动的，而图片 A 向左或者向上移动可以等价于图片 B 向右或者向下移动。因此，在对于每个位置 (x, y)，还要计算出 B 中所有点与 A (0,0) 重叠的 overlap。如下图所示：

Python3 实现：

class Solution:
    def largestOverlap(self, A: List[List[int]], B: List[List[int]]) -> int:
        max_ = 0
        N = len(A)
        for i in range(N):
            for j in range(N):
                max_ = max(max_, self.count(A, B, i, j))  # 向右或向下移动 A 到 (i, j)，计算重叠区域 overlap
                max_ = max(max_, self.count(B, A, i, j))  # 向右或向下移动 B 到 (i, j)（相当于向左或向上移动 A 到 (-i, -j)），计算重叠区域的 overlap
        return max_
    
    def count(self, A, B, x, y):  # 计算重叠区域的 overlap
        cnt = 0
        N = len(A)
        for i in range(x, N):
            for j in range(y, N):
                if A[i-x][j-y] == B[i][j] == 1:
                    cnt += 1
        return cnt

方法2（时间复杂度 O(n^2)，空间复杂度 O(n^2)）：

参考这篇文章 leetcode835引发的位距离思考，那么对于二维情况，我们同样去记录两幅图像 1 中的位置 (ax, ay)、(bx, by)，然后求出 A 和 B 中 1 的位置的各个差值 ((ax-bx), (ay-by))。差值出现次数最多的那个就是最大覆盖 overlap。

Python3 实现：

class Solution:
    def largestOverlap(self, A: List[List[int]], B: List[List[int]]) -> int:
        N = len(A)
        Apos = [(row, col) for row in range(N) for col in range(N) if A[row][col]]  # A中1的位置
        Bpos = [(row, col) for row in range(N) for col in range(N) if B[row][col]]  # B中1的位置
        sub = dict()  # 用字典对A和B中1的位置的差值计数
        max_ = 0
        for a in Apos:
            for b in Bpos:
                tem = (a[0]-b[0], a[1]-b[1])  # 计算A和B中1的位置的差值
                if tem not in sub:
                    sub[tem] = 1
                else:
                    sub[tem] += 1
                max_ = max(max_, sub[tem])  # overlap的最大值就是差值出现最多的次数
        return max_