密码学入门（6）：消息认证码

密码学入门（6）：消息认证码

上次讲到的单向散列函数只能保证数据传输的完整性，不能提供认证功能，即 Bob 不能确定消息是否来自 Alice，只能确定消息是完整的，没有被篡改。

假设有以下场景，现在 Alice 和 Bob 分别是两家银行：

• Alice 银行向 Bob 银行发送一条汇款请求：从账户 A 向账户 B 汇款1000万元。
• Bob 银行能保证收到的汇款请求与 Alice 银行所发送的内容完全一致，如果主动攻击者 Mallory 在中途将汇款请求进行了篡改，Bob 银行能识别出这种篡改。
• 但现在问题是，汇款请求到底是不是 Alice 银行发送的？有可能 Alice 银行根本就没有发送过汇款请求，而是由主动攻击者 Mallory 伪装成 Alice 银行发送的。

所以我们除了要关注汇款请求（消息）的“完整性”，还要关注“认证”问题，即“消息是否来自正确的发送者”。下面要介绍的消息认证码即能保证消息的完整性，还能对消息进行认证。

什么是消息认证码？

消息认证码（Message Authentication Code）是一种确认完整性并进行认证的技术，简称为MAC。

消息认证码的输入为任意长度的消息和一个发送者与接收者之间共享的密钥，它可以输出固定长度的数据，这个数据称为 MAC 值。

根据任意长度的消息输出固定长度的数据，这一点和单向散列函数很类似。但由于计算 MAC 值必须持有共享密钥，没有共享密钥的人就无法计算 MAC 值，因此消息认证码利用这一性质来完成认证。此外，消息认证码和单向散列函数一样具有雪崩效应，哪怕消息中发生$1$比特的变化，也会导致 MAC 值发生不可区分的改变。

消息认证码有多种实现方式，我们可以先简单的将其理解为：消息认证码是一种与密钥相关联的单向散列函数：

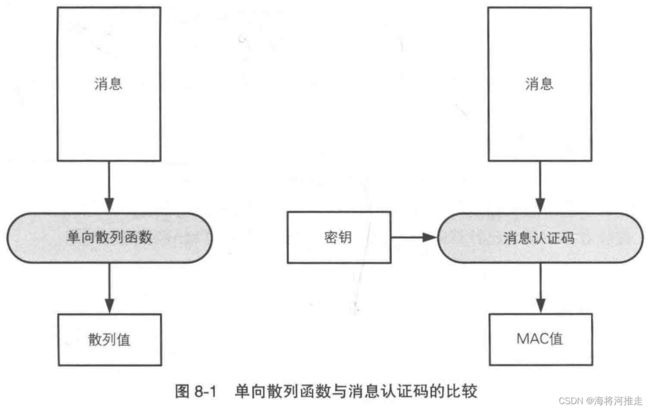
我们仍然假设 Alice 和 Bob 是两家银行，消息认证码的使用步骤如下：

消息认证码的密钥配送问题：由于发送者和接收者之间需要共享密钥，这一点和对称密码很相似。实际上，对称密码的密钥配送问题在消息认证码中同样会发生。要解决该问题，我们需要像对称密码一样使用一些共享密钥的方法，至于使用哪种配送方法，需要根据具体的目的来进行选择。

消息认证码的实现方式

使用 AES之 类的分组密码可以实现消息认证码。

我们将分组密码的密钥作为消息认证码的共享密钥来使用，并用 CBC 模式将消息全部加密，然后将最后一个密文分组用作 MAC 值。这是因为 CBC 模式的最后一个分组会受到整个消息以及密钥的双重影响，因此可以将它用作消息认证码。

下面我们来看一下使用单向散列函数实现的消息认证码：HMAC。

HMAC

HMAC是一种使用单向散列函数来构造消息认证码的方法，其中 HMAC 的 H 就是 Hash 的意思。

HMAC 中使用的单向散列函数并不局限于一种，任何高强度的单向散列函数都可以被用于 HMAC。例如用 SHA-256、SHA-512 所构造的 HMAC，分别称为 HMAC-SHA-256、HMAC-SHA-512。

HMAC 的步骤：

1. 密钥填充
   • 如果密钥比单向散列函数的分组长度要短，就在密钥的末尾填充$0$。
   • 如果密钥比分组长度长，则用单向散列函数求出密钥的散列值，然后将这个散列值用作HMAC的密钥。
2. 填充后的密钥与 ipad 的 XOR
   • 将填充后的密钥与被称为 ipad 的比特序列进行 XOR 运算。ipad 是将00110110（0x36）不断循环反复直到分组长度所形成的比特序列，其中 ipad 的 i 是 inner（内部）的意思。
   • XOR 运算所得到的值，就是一个和单向散列函数分组长度相同，且和密钥相关的比特序列，这个比特序列称为 ipadkey。
3. 与消息组合：将 ipadkey 附加在消息的开头。
4. 计算散列值：将$(3)$的结果输入单向散列函数，并计算出散列值。
5. 填充后的密钥与 opad 的 XOR
   • 将填充后的密钥与被称为 opad 的比特序列进行 XOR 运算。opad 是将01011100（0x5C）不断循环反复直到分组长度所形成的比特序列，其中 opad 的 o 是 outer（外部）的意思。
   • XOR 运算所得到的值也是一个和单向散列函数分组长度相同，且和密钥相关的比特序列，这个比特序列称为 opadkey。
6. 与散列值组合：将$(4)$的散列值拼在 opadkey 后面。
7. 计算散列值：将$(6)$的结果输入单向散列函数，并计算出散列值。这个散列值就是最终的MAC值。

通过上述流程我们可以看出，最后得到的 MAC 值，一定是一个和输入的消息以及密钥都相关的长度固定的比特序列。

此外，根据 RFC 2104，HMAC 的数学公式为：

$$\text{HMAC}(K,m)=H((K^{\prime }\oplus opad)||H((K^{\prime }\oplus ipad)||m\left)\right)$$

其中：

• $H$为密码散列函数（如SHA家族）
• $K$为密钥（secret key）
• $m$是要认证的消息
• $K^{\prime }$是从原始密钥K导出的另一个秘密密钥（如果$K$短于散列函数的输入块大小，则向右填充（Padding）零；如果比该块大小更长，则对K进行散列）
• || 代表串接
• ⊕ 代表异或（XOR）
• opad 是外部填充（0x5c5c5c…5c5c，一段十六进制常量）
• ipad 是内部填充（0x363636…3636，一段十六进制常量）

HMAC的伪代码如下：

function hmac (key, message) {
    if (length(key) > blocksize) {
        key = hash(key) // keys longer than blocksize are shortened
    }
    if (length(key) < blocksize) {
        // keys shorter than blocksize are zero-padded (where ∥ is concatenation)
        key = key ∥ [0x00 * (blocksize - length(key))] // Where * is repetition.
    }
   
    o_key_pad = [0x5c * blocksize] ⊕ key // Where blocksize is that of the underlying hash function
    i_key_pad = [0x36 * blocksize] ⊕ key // Where ⊕ is exclusive or (XOR)
   
    return hash(o_key_pad ∥ hash(i_key_pad ∥ message)) // Where ∥ is concatenation
}

认证加密

认证加密（AE或AEAD，Authenticated Encryption，Authenticated Encryption with Associated Data）是一种将对称密码与消息认证码相结合，同时满足机密性、完整性和认证三大功能的机制。常见的AEAD算法有chacha20-poly1305和aes-256-gcm。

认证加密的方法：

• Encrypt-then-MAC (EtM) ：先用对称密码将明文加密，然后计算密文的MAC值。
  
• Encrypt-and-MAC（E&M）：用对称密码将明文加密，并对明文计算MAC值。
  
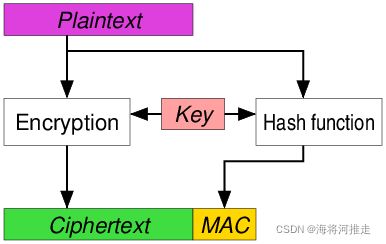
• MAC-then-Encrypt (MtE) ：先计算明文的MAC值，然后将明文和MAC值同时用对称密码加密。
  

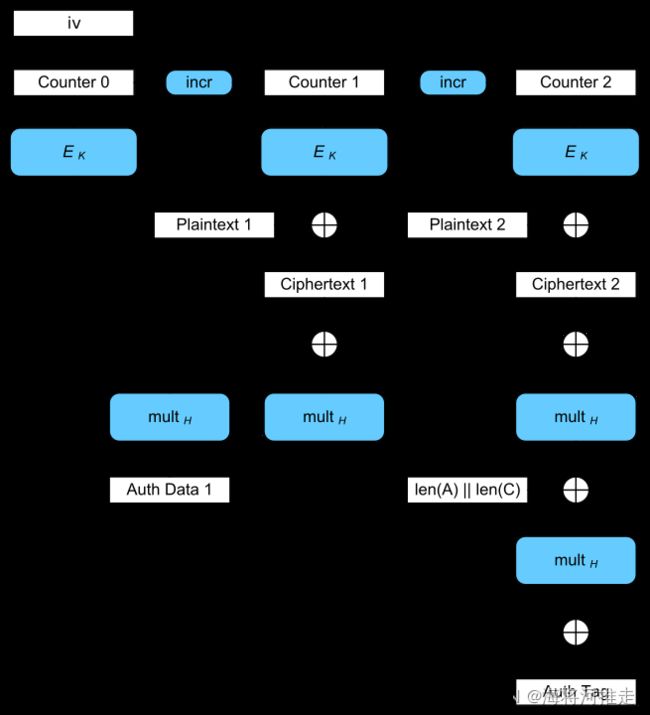
关于GCM：GCM（Galois/Counter Mode）是一种认证加密方式。GCM使用AES等128比特分组密码的CTR模式，并使用一个反复进行加法和乘法运算的散列函数来计算MAC值。由于CTR模式的本质是对递增计数器值进行加密，因此可通过对若干分组进行并行处理来提高运行速度。此外，由于CTR模式加密与MAC的值计算使用的是相同的密钥，因此在密钥管理方面也更容易。

重放攻击

我们仍然假设 Alice 和 Bob 是两家银行，现在有如下场景：

• Mallory 窃听到 Alice 银行与 Bob 银行之间的通信。
• Mallory 到 Alice 银行向自己在 Bob 银行中的账户 M 汇款 $100$ 万元。于是 Alice 银行生成了汇款请求信息，在计算出正确的 MAC 值后将 MAC 和消息一起发送给 Bob 银行。
• Bob 银行收到消息，确认消息是来自 Alice 银行的合法汇款请求，于是向账户 M 汇款 $100$ 万元。
• Mallory 将窃听到的汇款请求信息以及 MAC 值再次发送给 Bob 银行，此时 Bob 银行仍然会确认消息是来自 Alice 银行的合法汇款请求（误解），于是向账户 M 汇款 $100$ 万元。
• Mallory 将上一步过程重复 $100$ 次。
• 最后 Bob 银行向 M 账户累计汇入 $1$ 亿元，这时 Mallory 将这笔钱取出来。

在这里，Mallory 并没有破解消息认证码，而只是将 Alice 银行的正确 MAC 值保存下来重复利用而已。这种攻击方式称为重放攻击（replay attack）：

防御重放攻击的方式

• 序号：约定每次对发送的消息赋予一个递增的编号（序号，在发送完一条消息后递增），并在计算 MAC 值时将序号也包含在消息中。由于 Mallory 无法计算序号递增之后的 MAC 值，因此就可以防御重放攻击。
  • 问题：每次通信的发送方和接收方都需要知道初始的序号，如果接收方通过解析发送方发送的消息来获得序号，那么 Mallory 可以将从通信开始时的消息重放给接收方。
• 时间戳：约定在发送消息时包含当前时间，如果收到以前的消息，即便 MAC 值正确也将其当作错误的消息来处理，这样就能防御重放攻击。
  • 问题：接收方和发送方的时钟必须一致，并且因为通信的延迟，需要在时间的判断上留下缓冲，因此多多少少还是存在重放攻击的空间。
• nonce：在通信之前，发送方先向接收方发送一个一次性的随机数，这个随机数一般称为 nonce。每次通信时 nonce 的值都不一样，接收方只需要判断本次通信的 nonce 值是否在以往通信中出现过（为了做到这点，接收方需要存储最近 $n$ 次通信的 nonce 值，例如 $n=100$ 万次），即可防御重放攻击。
  • 为了判断 nonce 值是否在以往通信中出现过，我们需要一个高效的数据结构来存储和检查 nonce 值。布隆过滤器（Bloom Filter）可以做到这一点。ss 协议的官方实现就使用了这种方式抵御重放攻击。

消息认证码无法解决的问题

消息认证码无法解决的问题如下：

• 对第三方证明：假设 Bob 在接收了来自 Alice 的消息之后，无法向第三方验证者 Victor 证明这条消息的确是 Alice 发送的。
  • Victor 想要通过 MAC 值校验这条消息（Bob 相信 Victor，将密钥告诉了 Victor），因为 Alice 和 Bob 之间的密钥是共享的，所以 Bob 也可以生成 MAC 值，因此 Victor 无法判断这条消息是由 Alice 发送的。
• 防止否认：因为 Bob 无法向验证者 Victor 证明消息的确是 Alice 发送的，因此发送者 Alice 可以向 Victor 声称：“我没有向 Bob 发送过这条消息“ ”这条消息是 Bob 自己编的吧” “说不定 Bob 的密钥被主动攻击者 Mallory 给盗取了”。这种行为称为否认（repudiation），因此消息认证码无法防止否认（nonrepudiation）。

为了解决上面这两个问题，我们可以使用数字签名（将在之后介绍）。

参考

• 《图解密码技术》
• https://zh.wikipedia.org/wiki/HMAC
• https://zh.wikipedia.org/wiki/认证加密
• https://en.wikipedia.org/wiki/Galois/Counter_Mode