【学习笔记】密码学入门(2) 单向散列函数,消息认证码,数字签名,证书

【学习笔记】密码学入门(2) 单向散列函数,消息认证码,数字签名,证书

学习笔记 2 – 混合密码系统

在密码学入门(1)中提到了基本的密码形式,对称密码和公钥密码以及混合密码系统.

这一部分将学习到数字签名,证书,消息认证码,随机数生成器等.

单向散列函数

单向散列函数(one-way hash function),或哈希函数有一个输入和输出,输入称作消息(message),输出称作散列值(hash value).单向散列函数可以根据消息内容计算出散列值,散列值可以被用来检查消息完整性.具体哈希函数原理可看比特币的简单原理

散列值的长度和消息长度无关,例如SHA-256单向散列函数计算出的散列值永远是256bit.单向散列函数的性质有:

• 固定散列值长度
• 快速计算散列值
• 消息不同散列值不同
  两个不同的消息产生同一个散列值称作碰撞,所以单向散列函数需要具备抗碰撞性.所以得到一条散列值,要找到具备相同的散列值的另一条消息是很困难的.
  弱抗碰撞性:找到和特定消息具有相同的散列值的消息
  强抗碰撞性:找出任意消息但是具有相同散列值的两条消息
• 单向性

散列函数的应用:

• 检测软件是否被篡改
• 口令加密
• 消息认证
• 数字签名
• 伪随机数生成器
• 一次性口令

SHA函数

1995年NIST(美国国家标准技术研究所)发布的FIPS PUB 180-1称作SHA-1,可产生160bit散列值.SHA-256,SHA-384,SHA-512都是NIST设计的单向散列函数,统称SHA-2.SHA-1的强碰撞性于2005年攻破.

SHA-3单向散列函数2012年确定由Keccak算法作为SHA-3标准.SHA-3相比于SHA-2有完全不同的结构,适用于各种设备,包括嵌入式应用,硬件实现性能高,且相比于SHA-2 输入信息长度上限$2^{128}-1$,SHA-3没有长度限制.

Keccak算法采用海绵结构,下图中内部状态初始值为0,总共 $b=r+c$ bit. $f$函数是将输入的数据进行复杂的搅拌并输出结果,将输入消息进行分组 分成rbit的分组,先将内部状态的前r个bit和输入分组进行异或,再将内部状态的后c bit和异或后的r bit进行搅拌.r称为比特率,c称为容量,c bit不受输入分组的直接影响,输出仍然是b bit数据,容量c的意义在于防止将输入消息中的一些特征泄露出去.

其中f函数包括:
$\theta$:将每两列的各自5bit进行XOR,再置换原目标bit
$\rho$:lane方向bit平移
$\pi$:对slice进行bit平移
$\chi$:对相邻row进行取反求和
$l$:对整个state进行异或

对单向散列函数的攻击:
暴力破解:利用文件冗余性,修改文件不断尝试得到相同的散列值,针对弱抗碰撞性
生日攻击:找到任意两条具有相同散列值的消息,针对强抗碰撞性

但是单项散列函数能辨别篡改,不能辨别出伪装.

消息认证码

消息认证码(Message Authentication Code)是一种确认完整性并进行认证的技术,间成MAC值.
消息认证码的输入是任意长度的消息加上一个和接收者共享的密钥,输出为固定长度的数据,即MAC值.可以通过对比传输的MAC值和接收方通过密钥计算得到的MAC值对比证明认证成功.
输出固定长度,这点和单向散列函数相似;但是消息认证码需要输入共享的密钥.所以可以认为消息认证码(MAC)是一种与密钥相关联的单向散列函数.

消息认证码应用

IPsec:IPsec对互联网基本通信协议–IP协议增加安全性的一种方式,对通信内容的认证和完整性校验都是采用消息认证码完成.
SSL/TLS:SSL/TLS中对通信内容的完整性校验也使用了消息认证码.
HMAC:HMAC是一种使用哈希函数构造消息认证码的方法,把密钥和消息通过HASH函数生成MAC值.
$$HMAC=hash(opadkey\parallel hash(ipadkey\parallel mesage))$$

消息认证局限性

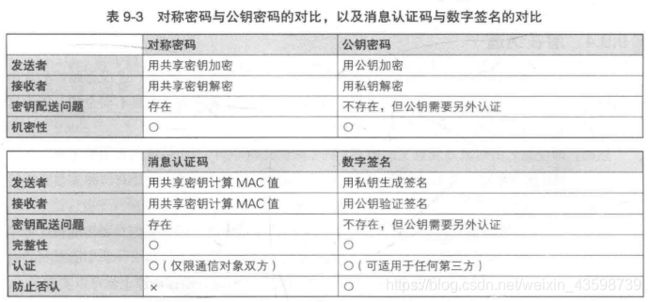
消息认证码可以解决篡改和伪装的问题,但是五分解决第三方证明和防止否认的问题.,可通过数字签名解决.

第三方证明:向第三方证明消息的准确性和完整性,因为MAC值是通过通信双方的密钥计算,对第三方无法证明消息的准确性.

防止否认:接收方可以通过MAC值确认消息来自发送方,但是如果发送方和接收方吵架了,发送方否认该消息正确性,接收方无法证明消息准确性,无法防止否认.

使用消息认证码可以识别篡改伪装行为,无法保证消息机密性和防止否认以及第三方证明.

数字签名

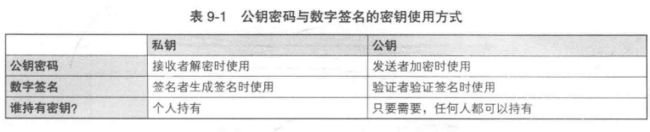
通过消息验证码发送者Alice和接收者Bob共享一个密钥,但是通过数字签名可以使用不同的密钥.Alice通过一个私钥生成签名,Bob可以使用公钥对Alice的签名进行验证,类似于签名提到的公钥密码反过来,私钥加密相当于生成密钥,公钥解密相当于验证签名.

数字签名的方法

• 直接对消息签名
• 对消息的散列值签名

后者它通过对消息的散列值进行加密,相比于对消息直接加密提高效率,有点类似混合密钥系统.把消息和特定的签名绑定在一起,就不用担心直接复制文件.
同时如果把签名部分提取出来,添加到其他消息后面,但是这个时候验证签名会失效.同时,因为该密文只有通过发送者加密产生,所以可以防否认.

数字签名的应用实例

• 安全信息公告
• 软件下载
• 公钥证书
• SSL/TLS(服务器证书)

RSA数字签名

RSA实现数字签名就是RSA加密的逆运算.

• RSA生成签名
  $$签名=消{息}^{D}modN$$
• RSA验证签名
  $$由签名得到的消息=签{名}^{E}modN$$
  D:　RSA解密用的私钥，用于加密数字签名
  E：RSA加密用的公钥，用于解密数字签名

对称密码和公钥密码的对比;消息认证码和数字签名的对比

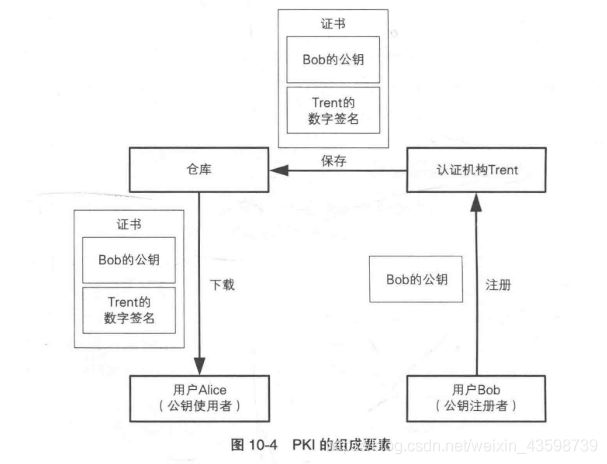
证书(Public-Key-Certificate)

公钥证书:由认证机构认定该公钥属于某个人的认定证书.

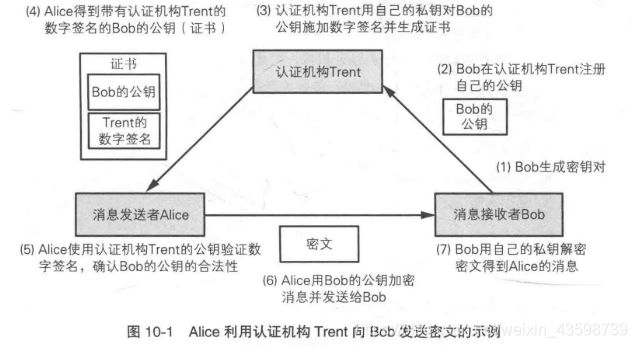
认证机构Trent会用自己的私钥加密发送者Bob的公钥施加数字签名并生成证书.发送者Alice会先通过Trent给的验证公钥验证数字签名,验证成功后便可得到Trent加密的发送方Bob的公钥,再通过公钥加密消息传输给接收者Bob.

公钥基础设施

公钥基础设施(Public-Key Infrastructure) 是有效运用公钥的一系列规范规格的统称,简称KPI.

组成要素

• 用户–使用KPI的人/实体entity
• 认证机构–颁发证书的人
• 仓库–保证证书的数据库

公钥注册者Bob:

• 生成密钥对
• 认证机构注册公钥
• 认证机构申请证书
• 申请作废已注册的公钥
• 解密接收的密文
• 对消息进行数字签名

公钥使用者Alice:

• 将消息加密后发送给接收者
• 验证数字密码

认证机构(CA):

• 生成密钥对(也可以由用户自己生成)
• Bob注册公钥时对本人身份进行认证
• 生成颁发证书
• 作废证书
• 作用:确保公钥的可信度,如果能保证公钥可信度,可不需要认证机构.

仓库(respository):
*保存证书

总结

• 单向散列函数
  数据指纹,确认数据一致性,防篡改,因为消息改变一点,便会引起散列值的巨大变化.但是无法防止伪装,所以需要认证,用于认证的技术就包括消息验证码(MAC)和数字签名.
• 消息认证码(MAC)
  消息认证码实在单向散列函数的基础上增加了一个对称密钥,没有密钥就无法计算出MAC值,所以可以通过MAC值判断消息来自发送方,防止伪装.但是无法对第三方证明和防止否认.
• 数字签名
  因为消息认证码使用对称密码,发送者和接收者共享密钥,所以无法防止发送方否认,类似于公钥算法,发送者可以用私钥加密签名,接收方可以通过公钥解密数字签名,也可以通过对消息的散列值进行数字签名,效率较高.但是我们无法确认接收者得到的公钥合法,防止得到不可靠的公钥,被中间人攻击,所以需要中间部门保证公钥的合法正确.
• 证书
  由认证机构通过私钥对发送者的公钥施加数字签名并生成证书保证公钥的正确性,在发送者验证了数字签名后可通过公钥加密信息发给接收者.

参考资料

[1] 图解密码技术(第三版)