置换检验是区别于参数检验进行t检验、卡方检验、方差分析,回归分析(参看前几节)的另一种思路方法;相比以前学过的参数法,置换检验更适合处理非正态数据,存在离群点,样本很小,或者无法做参数检验等情况,主要用于生成零假设的p值,即回答“效应是否存在”这样的问题;
自助法则主要针对潜在分布未知、出现离群点、样本量过小,或者没有可供选择的参数方法下,用于生成置信区间。比如像估计样本中位数的置信区间或者是两样本的中位数之差,而这些在正态分布理论没有简单公式理论套用。
置换检验
原理参考文章,主要思想我认为是求出所有分布的可能(中间的一般为零假设),出现这种分布的概率。
1、安装R包
(1)coin包为针对独立性问题的置换法检验包
install.packages("coin")
(2)lmPerm包为针对方差分析与回归分析的置换法检验包
- 因为作者已去世,源代码被CRAN归档,安装比较麻烦。
首先在 https://cran.r-project.org/src/contrib/Archive/lmPerm/ 下载lmPerm_1.1-2.tar.gz包文件;然后在https://cran.r-project.org/bin/windows/Rtools/ 下载并安装RTOOLs(Mac与Linux系统可以跳过此步);最后打开Rstudio,执行下述代码,选择lmPerm_1.1-2.tar.gz进行安装即可。
install.packages(file.choose(),repos = NULL,type="source")
2、coin 包的置换检验
2.1、t 检验--两组间差异
score <- c(40, 57, 45, 55, 58, 57, 64, 55, 62, 65)
treatment <- factor(c(rep("A",5), rep("B",5))) #一定要转化为因子
mydata <- data.frame(treatment, score) #要求是数据框格式
#比较A,B两组数据是否存在差异
- 一般参数法
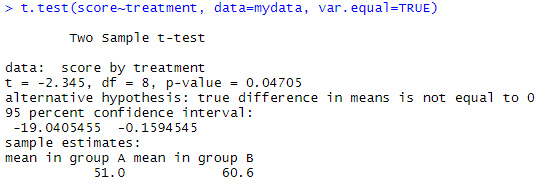
t.test(score~treatment, data=mydata, var.equal=TRUE)
#var.equal=TRUE 参数假定方差相等,并使用合并方差估计
#返回结果p值有显著意义
- 置换法
library(coin)
oneway_test(score~treatment, data=mydata, distribution="exact")
#返回结果p值无显著意义,教材作者认为由于观测数据少,还是更倾向于oneway_test置换检验法
distribution=参数可为exact(精确模式,即依据所有可能的排列组合,仅适用于两样本问题)、approxiamate(nresample=#)(蒙特卡洛抽样,#指需要重复的次数)、asymptotic(渐进分布抽样)
2.2、单因素方差分析--多组间差异
lmPerm包更擅长方差分析。示例实验设计仍为5组接受不同治疗方法的多组结果比较。
library(multcomp)
- 参数法
attach(cholesterol)
fit <- aov(response ~ trt)
summary(fit)
#返回结果p值有显著意义
- 置换法
set.seed(1234)
#因为有50个样本,不适合采用精确模式,本例使用了蒙特卡洛法抽样,为保证分享他人结果重现性,所以设置了随机数种子。
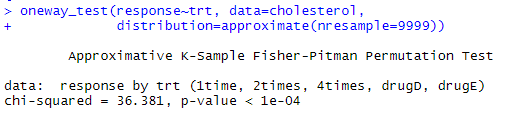
oneway_test(response~trt, data=cholesterol,
distribution=approximate(nresample=9999))
#返回结果p值有显著意义,但尴尬的是与教材结果不一致,与参数法的p值也有一定的差距。
值得注意的是定义重复次数的参数,教材中给的是B,可能由于版本更新,现在由nresample代替。
2.3、卡方检验--类别变量独立性检验
实验示例仍为关节炎的治疗(两种)与效果(无、部分、显著)间的关系
- 参数法
library(vcd)
mytable <- xtabs(~Treatment+Improved, data=Arthritis)
chisq.test(mytable)
#返回结果p值有显著意义
- 置换法
Arthritis <- transform(Arthritis,
Improved = as.factor(as.numeric(Improved)))
#Improved本身是一个有序因子,上述操作将其变成一个分类因子。
#若是有序因子,coin() 将会生成一个线性与线性趋势检验,而不是卡方检验
set.seed(1234)
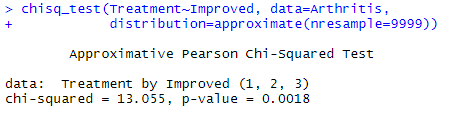
chisq_test(Treatment~Improved, data=Arthritis,
distribution=approximate(nresample=9999))
#返回结果p值有显著意义,且与参数法较接近。
-
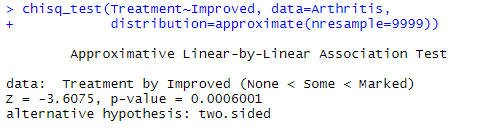
若不转换因子的趋势检验结果如下:
2.4、相关性检验
实验示例为研究文盲率与谋杀率是否相关
states <- as.data.frame(state.x77)
- 参数法
attach(states)
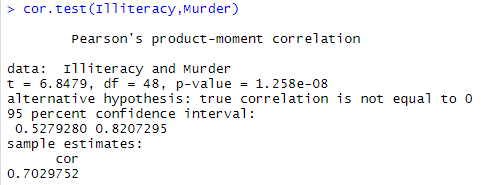
cor.test(Illiteracy,Murder)
detach(states)
#返回结果p值有显著意义,并且计算了相关系数
- 置换法
set.seed(1234)
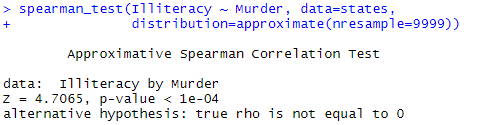
spearman_test(Illiteracy ~ Murder, data=states,
distribution=approximate(nresample=9999))
#仅计算p值,返回结果p值有显著意义(不计算相关系数)
3、lmPerm 包的置换检验
主要为lmp()、aovp()两个函数分别对应参数法的lm()线性回归、aov()方差分析。主要格式上的区别是添加了perm= 参数。可以为Exact(精确模式)、Prob(不断从可能的序列中抽样,直至估计的标准差在估计的p值0.1之下)、SPR(使用贯序概率比检验来判断何时停止抽样)。值得注意的是当样本观测大于10,perm="Exact"自动默认转为"Prob",因此精确检验只适用于小样本问题。
3.1、回归分析 lmp
(1)简单线性回归
实验示例仍为以身高预测体重的设计
- 参数法
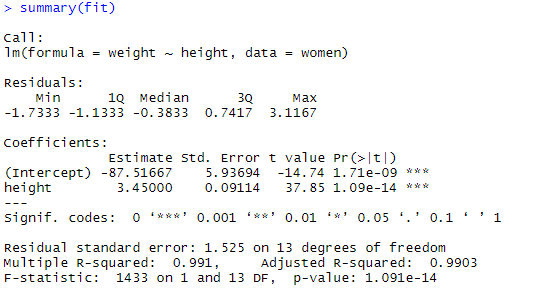
fit <- lm(weight ~ height, data=women)
summary(fit)
#返回回归系数结果p值有显著意义
- 置换法
library(lmPerm)
set.seed(1234)
fit1 <- lmp(weight ~ height, data=women, perm="Prob")
summary(fit1)
#返回回归系数结果p值有显著意义,好像不显示截距项值
(2)多项式回归
高精度拟合身高体重回归关系
- 参数法
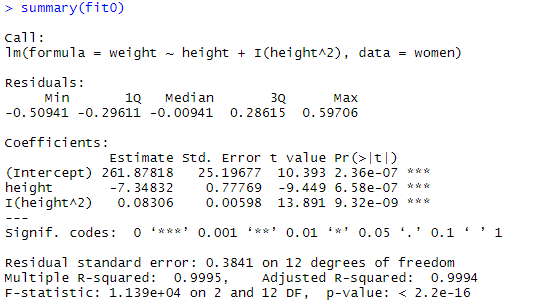
fit0 <- lm(weight ~ height + I(height^2), data=women)
summary(fit0)
- 置换法
library(lmPerm)
set.seed(1234)
fit <- lmp(weight ~ height + I(height^2), data=women, perm="Prob")
summary(fit)
(3)多元回归
探究谋杀率与多因素的回归关系
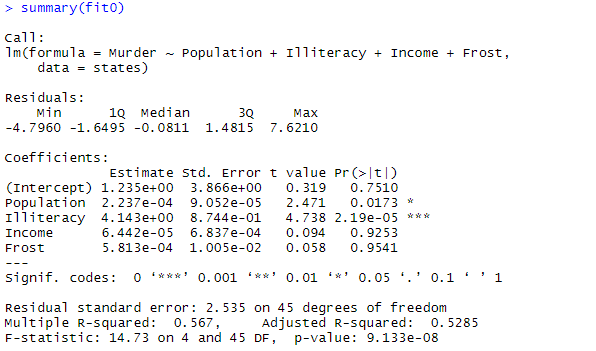
- 参数法
states <- as.data.frame(state.x77)
fit0 <- lm(Murder ~ Population + Illiteracy + Income + Frost, data=states)
summary(fit0)
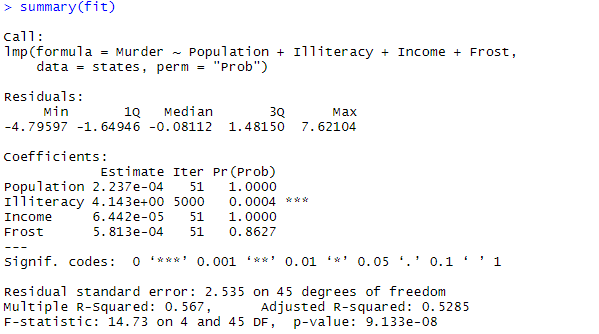
- 置换法
set.seed(1234)
fit <- lmp(Murder ~ Population + Illiteracy+Income+Frost,data=states, perm="Prob")
summary(fit)
3.2、方差分析 aovp
(1)单因素方差分析
- 参数法及coin包oneway_test()函数方法见上 2.2
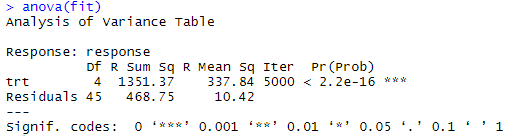
- aovp()置换法
library(lmPerm)
library(multcomp)
set.seed(1234)
fit <- aovp(response ~ trt, data=cholesterol, perm="Prob")
anova(fit)
#返回p值具有显著意义,表明各组的疗法效果不全相同
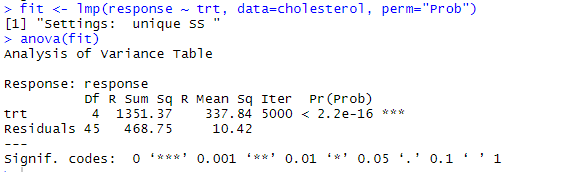
有意思的是教材随送的参考代码如下,即aovp被替换成lmp,但做出来的结果与上面一模一样,发现下面两点也有相同的问题........存疑!
fit <- lmp(response ~ trt, data=cholesterol, perm="Prob")
(2)单因素协方差分析
实验示例仍为药物对刚出生小鼠体重影响,协变量为怀孕时间
- 参数法
library(multcomp)
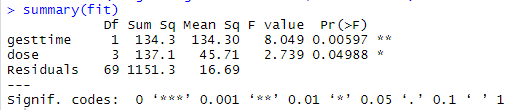
fit <- aov(weight ~ gesttime + dose, data=litter)
summary(fit)
#结果表明控制怀孕时间相同时,不同药物对小鼠体重的影响不同
- 置换法
set.seed(1234)
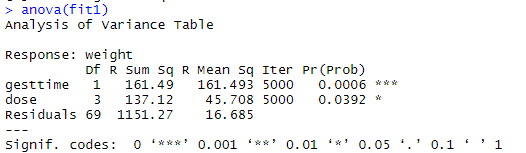
fit1 <- aovp(weight ~ gesttime + dose, data=litter, perm="Prob")
anova(fit1)
#结果同上
(3)双因素方差分析(交互效应)
实验示例:两种药物分别在不同剂量下对小鼠牙齿长度的影响。
- 参数法
fit <- aov(len ~ supp*dose, data=ToothGrowth)
summary(fit)
- 置换法
set.seed(1234)
fit1 <-aovp(len ~ supp*dose, data=ToothGrowth, perm="Prob")
anova(fit1)
自助法求置信区间
核心思想是有放回的抽样多次(1000次)
1、一般步骤
(1)写一个能返回带研究统计量的函数;
(2)确定重复数,使用boot()函数处理;(一般重复1000次即可;此外有人认为初始样本大小为20-30即可得到足够好的结果);
(3)boot.ci()函数计算统计量置信区间。
在回归分析中,confint()函数用于提供回归系数的置信区间(95%)
2、单个统计量自助法
实验示例:使用mtcar数据框,采用多元回归,根据车重和发动机排量来预测汽车的每加仑行驶的英里数。想获得95%的R平方值(预测变量对响应变量可解释的方差比)的置信区间
(1)首先写函数
rsq <- function(formula, data, indices) { #固定格式
d <- data[indices,] #固定格式;必须声明,因为boot() 要用其来选择样本
fit <- lm(formula, data=d) #计算公式
return(summary(fit)$r.square) #返回特定值
}
(2)然后使用boot()函数
library(boot)
set.seed(1234)
results <- boot(data=mtcars, statistic=rsq,
R=1000, formula=mpg~wt+disp)
#分别为数据框、函数、重复次数,供函数使用的公式
#可以进一步查看results结果
results$t0 #中心值
results$t #所有枚举值
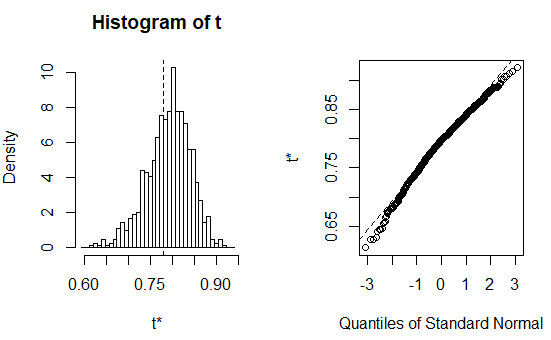
print(results)
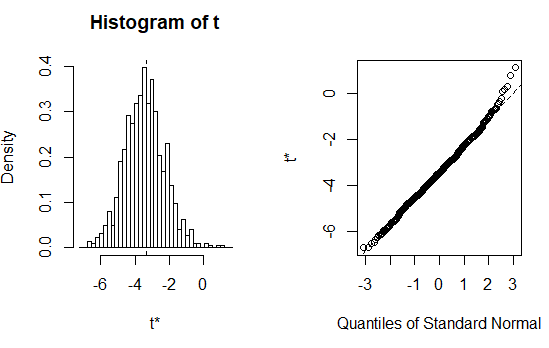
plot(results) #绘制结果,看出自助R方值不呈正态分布
(3)最后boot.ci()函数求置信区间
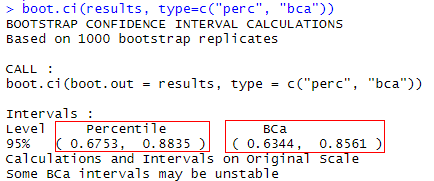
boot.ci(results, type=c("perc", "bca"))
- type参数设定了获取置信区间的方法,perc方法展示的是样本均值;bca将根据偏差对区间做简单调整。作者认为一般bca的结果更可取。
3、多个统计量自助法
实验示例:使用mtcar数据框,采用多元回归,根据车总和发动机排量来预测汽车的每加仑行驶的英里数。想获取一个统计量向量--三个回归系数(截距项、车总、发动机排量)95%的置信区间。
#首先还是写函数,返回回归系数向量(三个统计量)
bs <- function(formula, data, indices) {
d <- data[indices,] #注意格式
fit <- lm(formula, data=d)
return(coef(fit))
}
library(boot)
set.seed(1234)
results <- boot(data=mtcars, statistic=bs,
R=1000, formula=mpg~wt+disp)
results$t0 #中心值
results$t #所有枚举值
print(results)
plot(results, index=2)
#索引index1,2,3分别指截距项、车重,发动机排量
boot.ci(results, type="bca", index=2)
boot.ci(results, type="bca", index=3)
本次主要学习了区别于参数法的实验分析思路--置换检验;以及一个求置信区间的利器--自助法。
参考教材《R语言实战(第2版)》