PyTorch深度学习实践概论笔记11-卷积神经网络高级篇

在文章PyTorch深度学习实践概论笔记10-卷积神经网络基础篇介绍了卷积神经网络基础，接下来这一讲介绍高级一点的卷积神经网络。

上一讲介绍的卷积神经网络和再之前介绍的多层感知机、全连接网络，它们在架构上是串行的结构（上一层的输出是下一层的输入）。但是，在神经网络里面有很多更为复杂的结构，比如加上分支，或者输出会返回来。接下来介绍两种比较复杂的网络如何实现。

0 Revision

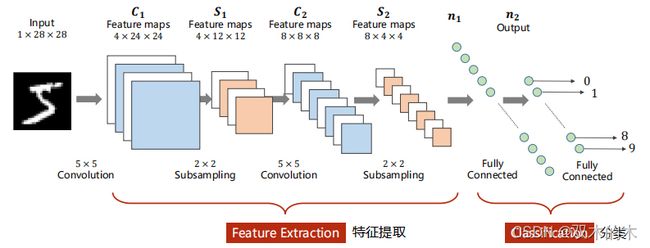
之前讲过的这个网络非常近似LeNet5。

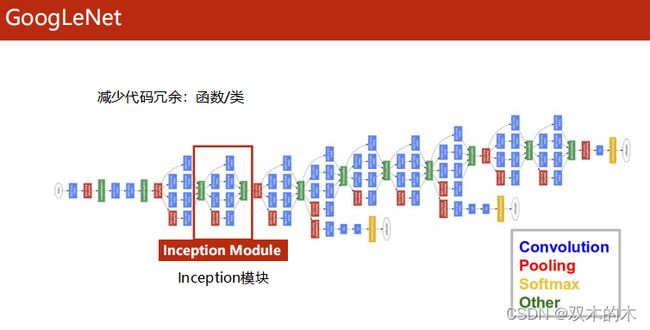
1 GoogLeNet

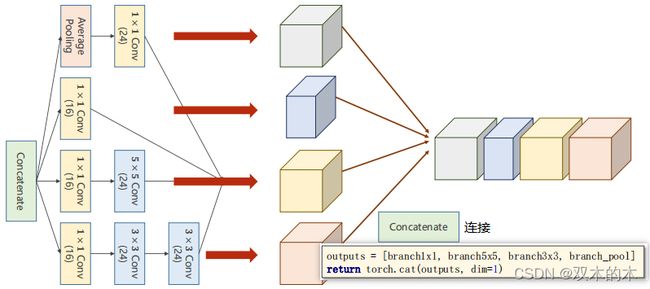
上图中蓝色的块是卷积层，红色的块是池化层，黄色的块是Softmax输出，绿色是拼接层。在编程中，要减少代码冗余，有两种常用的方法：使用函数和类。对于上图中相似的结构我们可以封装起来。

1.1 Inception Module

这个块：Inception（盗梦空间）

一般网络需要自己选kernel的大小（超参数），GoogLeNet的思想是我们不知道选什么大小的卷积核，就都用一下，然后合并在一起，如果3*3的比较好用，这样权重自然会比较大。这里的思想是提供几种候选的卷积神经网络的配置，之后通过训练自动的找到最优的组合。

Concatenate是指把张量沿着通道拼接起来，经过不同方式的输出保证W和H一样（b,c,w,h）。

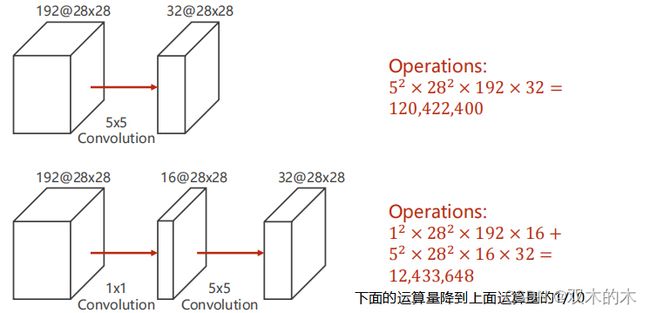
接下来考虑1x1的卷积，这种卷积有啥用？（降低运算量）

1.1.1 What is 1x1 convolution?

1*1卷积的个数取决于输入张量的通道。接下来看计算过程： 

输入是CxWxH，经过C个1*1卷积，输出是1xWxH；经过C*m个1*1卷积，输出是mxWxH。1*1卷积完成了一个信息融合。

所以1x1卷积最主要的工作：改变通道数，减小复杂度。

1.1.2 Why is 1x1 convolution?

1*1卷积可以减少运算量，第二行使用1*1卷积的运算量只有上一行的1/10。

1.2 Implementation of Inception Module

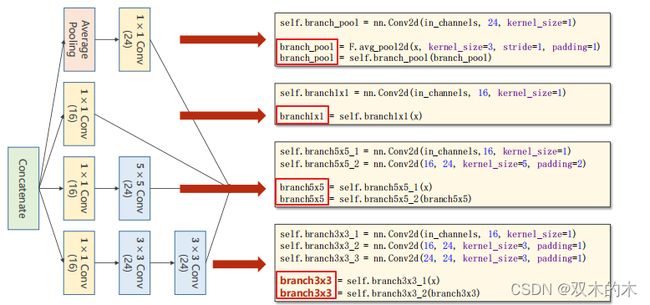
 下面看看Inception如何实现的。

（上图最后一行少了branch = self.branch3x3_3(branch3x3)，因为ppt写不下了）

在各个组合完成之后还需要拼接，图示化如下：

注意括号里的数字是通道数（24,16）。代码torch.cat(outputs,dim=1)中dim=1是指沿着通道C进行拼接（b,c,w,h）。

整合的代码如下：

class InceptionA(nn.Module):

    def __init__(self, in_channels):

    	super(InceptionA, self).__init__()

    	self.branch1x1 = nn.Conv2d(in_channels, 16, kernel_size=1)

    	
     	self.branch5x5_1 = nn.Conv2d(in_channels,16, kernel_size=1)

    	self.branch5x5_2 = nn.Conv2d(16, 24, kernel_size=5, padding=2)


    	self.branch3x3_1 = nn.Conv2d(in_channels, 16, kernel_size=1)

    	self.branch3x3_2 = nn.Conv2d(16, 24, kernel_size=3, padding=1)

    	self.branch3x3_3 = nn.Conv2d(24, 24, kernel_size=3, padding=1)

    
    	self.branch_pool = nn.Conv2d(in_channels, 24, kernel_size=1)


    def forward(self, x):

    	branch1x1 = self.branch1x1(x)
     

    	branch5x5 = self.branch5x5_1(x)

    	branch5x5 = self.branch5x5_2(branch5x5)
     

    	branch3x3 = self.branch3x3_1(x)

    	branch3x3 = self.branch3x3_2(branch3x3)

    	branch3x3 = self.branch3x3_3(branch3x3)
     

    	branch_pool = F.avg_pool2d(x, kernel_size=3, stride=1, padding=1)

    	branch_pool = self.branch_pool(branch_pool)

    	outputs = [branch1x1, branch5x5, branch3x3, branch_pool]

    	return torch.cat(outputs, dim=1)

注意初始的输入通道没有写死，而是作为in_channels入参设置。

1.3 Using Inception Module

构造网络的代码如下：

class Net(nn.Module):

    def __init__(self):

    	super(Net, self).__init__()

    	self.conv1 = nn.Conv2d(1, 10, kernel_size=5)

    	self.conv2 = nn.Conv2d(88, 20, kernel_size=5)  #24+16+24+24=88


    	self.incep1 = InceptionA(in_channels=10)

    	self.incep2 = InceptionA(in_channels=20)


    	self.mp = nn.MaxPool2d(2)

    	self.fc = nn.Linear(1408, 10)  #写代码为了准确最好不手算1048
     

    def forward(self, x):

    	in_size = x.size(0)

        	x = F.relu(self.mp(self.conv1(x)))

        	x = self.incep1(x)

       	x = F.relu(self.mp(self.conv2(x)))

        	x = self.incep2(x)

        	x = x.view(in_size, -1)

        	x = self.fc(x)

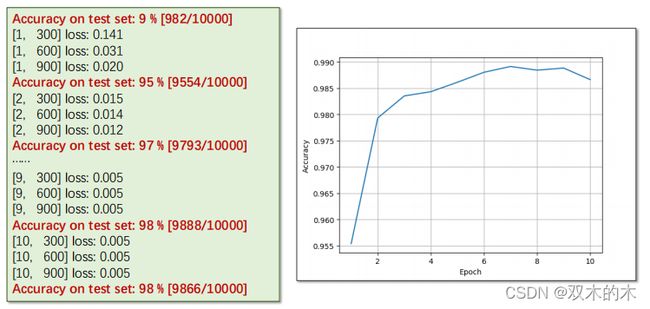
        	return x

结果：

这里性能提高不多，主要原因还是背后的全连接层，不过我们重点看的是改变卷积层的结构来提高性能。 

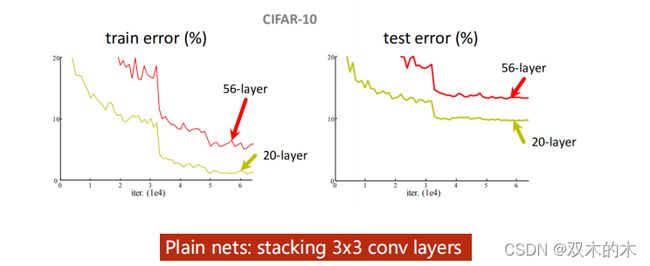
2 Can we stack layers to go deeper?

上图表明20层的卷积要比56层的好，可能是因为56层的没有优化好（梯度消失）。 

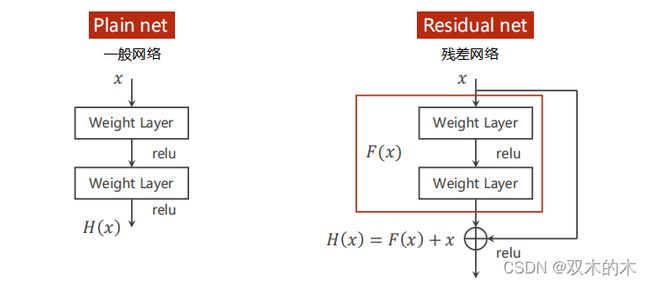
2.1 Residual Network

2.2 Implementation of Residual Block

代码实现如下：

class ResidualBlock(nn.Module):

    def __init__(self, channels):

    	super(ResidualBlock, self).__init__()

    	self.channels = channels

    	self.conv1 = nn.Conv2d(channels, channels, kernel_size=3, padding=1)  #padding=1保证输入输出大小不变

    	self.conv2 = nn.Conv2d(channels, channels, kernel_size=3, padding=1)


    def forward(self, x):

    	y = F.relu(self.conv1(x))#上图的F(x)

    	y = self.conv2(y)

    	return F.relu(x + y)#上图的H(x)=F(x)+x

2.3 Implementation of Simple Residual Network

代码如下：

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(1, 16, kernel_size=5)
        self.conv2 = nn.Conv2d(16, 32, kernel_size=5)
        self.mp = nn.MaxPool2d(2)
        self.rblock1 = ResidualBlock(16)
        self.rblock2 = ResidualBlock(32)
        self.fc = nn.Linear(512, 10)
    
    def forward(self, x):
        in_size = x.size(0)
        x = self.mp(F.relu(self.conv1(x)))
        x = self.rblock1(x)
        x = self.mp(F.relu(self.conv2(x)))
        x = self.rblock2(x)
        x = x.view(in_size, -1)
        x = self.fc(x)
        return x

在网络设计的时候最重要的是：你在设计的时候，网络的超参数，以及输入和输出（之后测试的时候可以输出每一步的张量，进行核实）。

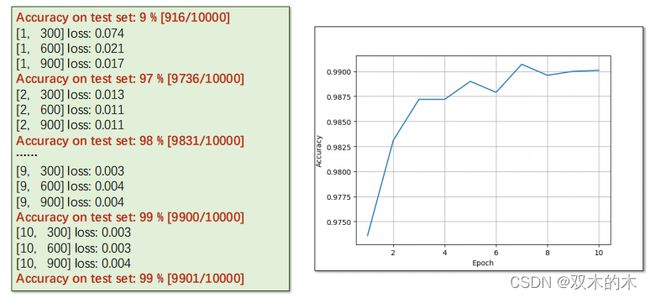
结果输出：

使用Residual network在测试集上的准确率为99%。

3 Exercise

3.1 Exercise 11-1: Reading Paper and Implementing ResNet

课后练习1：应用其它的Residual Block

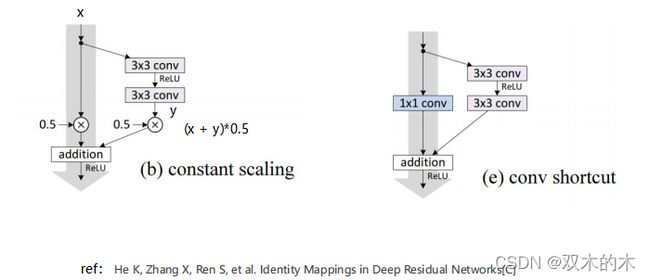
ref：He K, Zhang X, Ren S, et al. Identity Mappings in Deep Residual Networks[C]

3.2 Exercise 11-2: Reading and Implementing DenseNet

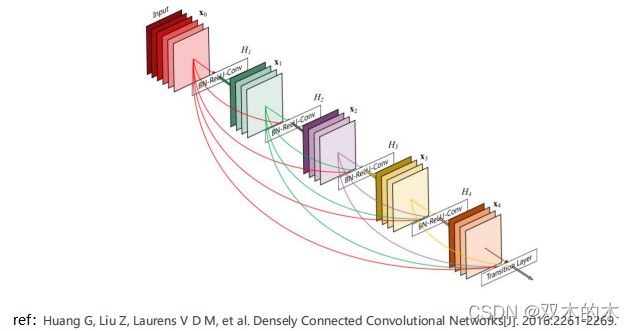
课后练习2：应用DenseNet网络，上一层的输出不仅提供给下一层，甚至下面几层。

ref：Huang G, Liu Z, Laurens V D M, et al. Densely Connected Convolutional Networks[J]. 2016:2261-2269

练习之后会更新，请看评论区。

4 Conclusion

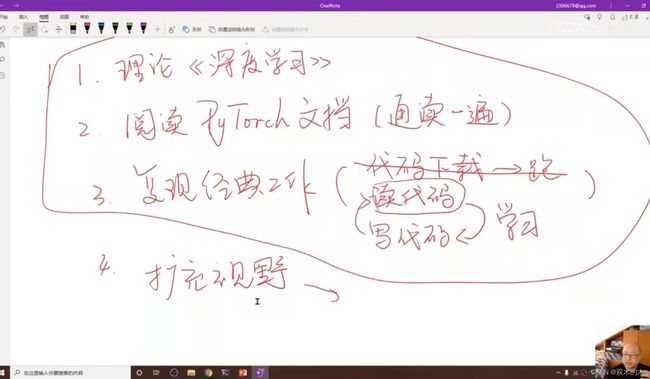
关于图像的处理老师先介绍这么多，看看老师的几点建议：

• 第一步：理论的学习，看《深度学习》花书
• 第二步：在开发中，如果将来要写一些更复杂的网络，建议阅读PyTorch文档（内容不多，通读一遍）
• 第三步：复现一些经典工作（找到论文——读代码——写代码——读代码——写代码....），只是下载代码然后跑通没有什么意义
• 第四步：选一个特定领域，大量阅读论文，看看常用技巧，想各种创新点，注意扩充视野（提前是拥有前几步的能力）

深度学习相对来说对数学的要求不是特别高，入门比较简单，但是在某一领域是需要长时间的积累的。

说明：记录学习笔记，如果错误欢迎指正！写文章不易，转载请联系我。