人工智能入门学习笔记(三)(PyTorch)
人工智能入门学习笔记(三)
- 项目:Purdue University BME595课程作业
- Homework03——Artificial Neural Network - Back-Propagation pass
-
- 代码、输出结果、结果分析图
-
- 代码
- 结果输出:
- 结果分析图:
- 知识框架
-
- 原理概述
- 损失函数
-
- MSE(Mean Square Error) 均方误差
- CE(Cross Entropy) 交叉熵
-
- 信息量
- 熵
- 相对熵(KL散度)
- 交叉熵
- Back-Propagation
-
- Gradient Descent
- 程序详解
-
- 前向传播
- 反向传播
- 总结
项目:Purdue University BME595课程作业
这个项目是一位朋友向我推荐的入门学习用的,是在Github上下载的其他学生的作业,由于找不到作业要求,只有一个程序,所以每一个作业的目的,以及如何去理解这个程序都是我自己逆推出来的,加之这是一份学习笔记,我也是初学此道,是以如果出现错误以及缺漏之处,还望诸位不吝赐教。
附参考程序:https://github.com/soumendukrg/BME595_DeepLearning
这位老哥的程序是我找了几个做对比后,相对而言readme写的较为详尽,且程序注释较多的一个。
另外,这是我第一次写博客分享学习笔记,也不太清楚是否会构成对这个项目亦或者这个老哥的程序的侵权什么的,如果有我会立刻修改。
附:
Homework01 传送门
Homework02 传送门
Homework03——Artificial Neural Network - Back-Propagation pass
本次作业的目的在于通过手动编写一个反向传播的代码以实现对 w e i g h t weight weight和 b i a s bias bias的自动取值,并与第二次作业的取值进行比较。
代码、输出结果、结果分析图
代码
# test.py
from logic_gates import AND
from logic_gates import XOR
# 创建与门和异或门的类 并对其进行训练
And = AND()
And.train()
Xor = XOR()
Xor.train()
# 与门
print("\nDemonstrating AND Gate functionality using FeedForward Neural Network")
print("And(False, False) = %r" % And(False, False))
print("And(False, True) = %r" % And(False, True))
print("And(True, False) = %r" % And(True, False))
print("And(True, True) = %r" % And(True, True))
# 异或门
print("\nDemonstrating XOR Gate functionality using FeedForward Neural Network")
print("Xor(False, False) = %r" % Xor(False, False))
print("Xor(False, True) = %r" % Xor(False, True))
print("Xor(True, False) = %r" % Xor(True, False))
print("Xor(True, True) = %r" % Xor(True, True))
# logic_gates.py
from neural_network import NeuralNetwork
import torch
import numpy as np
class AND:
def __init__(self):
self.and_gate = NeuralNetwork([2, 1])
self.max_iter = 100000
def __call__(self, x: bool, y: bool):
self.x = x
self.y = y
output = self.and_gate.forward(torch.FloatTensor([[self.x], [self.y]]))
return bool(np.around(output.numpy()))
def train(self):
print("\nStarting training Network for AND Gate")
# 创建训练用的数据集
dataset = torch.FloatTensor([[0, 0], [0, 1], [1, 0], [1, 1]])
# 创建用来存储目标结果的4*1大小的张量
target_data = torch.zeros((len(dataset), 1), dtype=torch.int)
# 使用数据集对模型进行反复训练
for i in range(self.max_iter):
# 打乱原始数据集的顺序以生成多组训练数据
indices = torch.randperm(4)
train_data = torch.index_select(dataset, 0, indices)
# 找到训练数据对应的目标结果
for j in range(len(dataset)):
target_data[j] = train_data[j, 0] and train_data[j, 1]
# 开始训练
if self.and_gate.total_loss > 0.01: # 若total_loss比0.01大则继续训练
output = self.and_gate.forward(train_data) # 进行正向过程(Forward pass)以得到各层的输入元素 即(偏z/偏w)
# 此处可选择 MSE CE 损失函数
self.and_gate.backward(target_data, "MSE") # 进行反向过程(Backward pass)以得到(偏loss/偏w)
self.and_gate.updateParams(0.5) # 更新权重张量 learning_rate设置为1
else:
print("Training completed in %d iterations\n" % i)
break # 此时表示total_loss已经小于0.01 可以跳出循环了
old_weights = torch.FloatTensor([[-30, 20, 20]])
new_weights = self.and_gate.getLayer(0)
print("Manually set Weights: %r\n Newly learned Weights %r\n" % (old_weights, new_weights))
class XOR:
def __init__(self):
self.xor_gate = NeuralNetwork([2, 2, 1])
self.max_iter = 1000000
def __call__(self, x: bool, y: bool):
self.x = x
self.y = y
output = self.xor_gate.forward(torch.FloatTensor([[self.x], [self.y]]))
return bool(np.around(output.numpy()))
def train(self):
print("\nStarting training Network for XOR Gate")
# 创建训练用的数据集
dataset = torch.FloatTensor([[0, 0], [0, 1], [1, 0], [1, 1]])
# 创建用来存储目标结果的4*1大小的张量
target_data = torch.zeros((len(dataset), 1), dtype=torch.int)
# 使用数据集对模型进行反复训练
for i in range(self.max_iter):
# 打乱原始数据集的顺序以生成多组训练数据
indices = torch.randperm(4)
train_data = torch.index_select(dataset, 0, indices)
# 找到训练数据对应的目标结果
for j in range(len(dataset)):
target_data[j] = (train_data[j, 0] and (not train_data[j, 1])) or (
(not train_data[j, 0]) and train_data[j, 1])
# 开始训练
if self.xor_gate.total_loss > 0.01: # 若total_loss比0.01大则继续训练
output = self.xor_gate.forward(train_data) # 进行正向过程(Forward pass)以得到各层的输入元素 即(偏z/偏w)
self.xor_gate.backward(target_data, "MSE") # 进行反向过程(Backward pass)以得到(偏loss/偏z)
self.xor_gate.updateParams(0.5) # 更新权重张量 learning_rate设置为5
else:
print("Training completed in %d iterations\n" % i)
break # 此时表示total_loss已经小于0.01 可以跳出循环了
old_weights1 = torch.FloatTensor([[-50, 60, -60], [-50, -60, 60]])
old_weights2 = torch.FloatTensor([[-50, 60, 60]])
new_weights1 = self.xor_gate.getLayer(0)
new_weights2 = self.xor_gate.getLayer(1)
print("Manually set Weights: %r %r\n Newly learned Weights %r %r\n" % (
old_weights1, old_weights2, new_weights1, new_weights2))
# neural_network.py
import numpy as np
import torch
import math
class NeuralNetwork:
def __init__(self, layers_list: list):
self.layers_list = layers_list
self.weights = {} # 权重
self.partial_loss_w = {} # (偏loss/偏w)
self.z = {} # 字典z用来存储input和weights的乘积 也是sigmoid函数的输入值
self.a = {} # 字典a用来存储sigmoid函数的输出值
# 设置字典的键值
self.key = ["" for x in range(len(self.layers_list) - 1)]
for i in range(len(self.layers_list) - 1):
self.key[i] = "(layer" + str(i) + "-layer" + str(i + 1) + ")"
# 创建一个符合需求大小的初始权重张量 其内的元素从正态分布中随机取出作为初始值
for i in range(len(self.layers_list) - 1):
self.weights[self.key[i]] = torch.from_numpy(np.random.normal(0, 1 / math.sqrt(self.layers_list[i]), (
self.layers_list[i + 1], self.layers_list[i] + 1))).type(torch.FloatTensor)
self.total_loss = 0.1 # 设置total_loss的初始值
def getLayer(self, layer: int):
# 将所需层的权重矩阵传递出去
self.layer = layer
return self.weights[self.key[layer]]
def forward(self, input: torch.FloatTensor):
# 传入的训练数据为4*2 传入的测试数据为2*1
(r, c) = input.size()
if c != 1:
# 进入此if则说明为训练数据 则对其进行转置 转化为2*4
self.input = input.t()
else:
# 进入此else则说明为测试数据 保留原2*1
self.input = input
(row, col) = self.input.size()
bias = torch.ones((1, col))
bias = bias.type(torch.FloatTensor)
# a[0]存储输入层的输入数据
self.a[0] = self.input
for i in range(len(self.layers_list) - 1):
self.a[i] = torch.cat((bias, self.a[i]), 0) # 将bias和输入数组合并到一起
weights = self.weights[self.key[i]] # 取出权重矩阵
self.z[i + 1] = torch.mm(weights, self.a[i]) # 存储下一层的z
self.a[i + 1] = torch.sigmoid(self.z[i + 1]) # 存储下一层的a
return self.a[len(self.layers_list) - 1].t()
# MSE CE
def backward(self, target: torch.FloatTensor, loss: str):
self.target = target.t()
if loss == 'MSE':
# loss function使用MSE 即Mean Square Error
# loss = (1 / n) * Sigma[ (y - y_hat)^2 ]
self.total_loss = ((self.a[len(self.layers_list) - 1] - self.target).pow(2).sum()) / (len(target))
# (偏loss/偏a) = (1 / n) * Sigma[ (a - a_hat) ] 矩阵大小为1*4
partial_loss_a = (self.a[len(self.layers_list) - 1] - self.target) / len(target)
# (偏a/偏z) = sigmoid'(z) = a * (1 - a) 矩阵大小为1*4
partial_a_z = self.a[len(self.layers_list) - 1] * (1 - self.a[len(self.layers_list) - 1])
# (偏loss/偏z) = mul( (偏loss/偏a), (偏a/偏z) )
partial_loss_z = torch.mul(partial_loss_a, partial_a_z)
print(partial_loss_z.shape)
else:
# loss function使用CE 即Cross Entropy
negation_target_sup = torch.tensor([[1, 1, 1, 1]], dtype=torch.int32)
negation_target = (negation_target_sup - self.target).type(torch.float)
ln_a = np.log(self.a[len(self.layers_list) - 1])
negation_a_sup = torch.tensor([[1.0, 1.0, 1.0, 1.0]])
negation_ln_a = np.log(negation_a_sup - self.a[len(self.layers_list) - 1])
# loss = -Sigma[ y_hat * ln(y) + (1 - y_hat) * ln(1 - y) ]
self.total_loss = (-1) * ((torch.mm(ln_a, self.target.type(torch.float).t()) + torch.mm(negation_ln_a, negation_target.t())).sum())
# (偏loss/偏a) = Sigma[ (a - a_hat) / (a * (1 - a)) ] 矩阵大小为???
# 激活函数为sigmoid (偏a/偏z) = a * (1 - a) 矩阵大小为1*4
# 故可直接计算 (偏loss/偏z) = Sigma[ (a - a_hat) ]
partial_loss_z = self.a[len(self.layers_list) - 1] - self.target
print(partial_loss_z.shape)
for i in range(len(self.layers_list) - 2, -1, -1):
if i < len(self.layers_list) - 2:
# 输出层(偏loss/偏z)的矩阵大小为1*4
# 隐含层(偏loss/偏z)的矩阵大小为3*4
# 故将其中bias对应的那一项删去 仅保留weights相关的(偏loss/偏z)
indices = torch.LongTensor([1, 2])
partial_loss_z = torch.index_select(partial_loss_z, 0, indices)
# (偏loss/偏w) = (偏loss/偏a) * (偏a/偏z) * (偏z/偏w)
# 输出层(偏loss/偏w)的矩阵大小为3*1
# 隐含层(偏loss/偏w)的矩阵大小为3*2
self.partial_loss_w[i] = torch.mm(self.a[i], partial_loss_z.t())
partial_a_z = self.a[i] * (1 - self.a[i])
# (偏loss/偏z)[前一层] = (偏loss/偏z)[当前层] * (偏z/偏a)[当前层z比前一层a 即weights] * (偏a/偏z)[前一层]
partial_loss_a = torch.mm(self.weights[self.key[i]].t(), partial_loss_z)
# (偏loss/偏z)的矩阵大小为3*4
partial_loss_z = torch.mul(partial_loss_a, partial_a_z)
def updateParams(self, eta: float):
self.eta = eta
for i in range(len(self.layers_list) - 1):
# weights* = weights - eta * gradient
gradient = torch.mul(self.partial_loss_w[i], self.eta)
self.weights[self.key[i]] = self.weights[self.key[i]] - gradient.t()
结果输出:
A
损失函数loss function: MSE
学习速率η: 0.5

B
损失函数loss function: CE
学习速率η: 0.5

C
损失函数loss function: MSE
学习速率η: 0.75

D
损失函数loss function: CE
学习速率η: 0.75

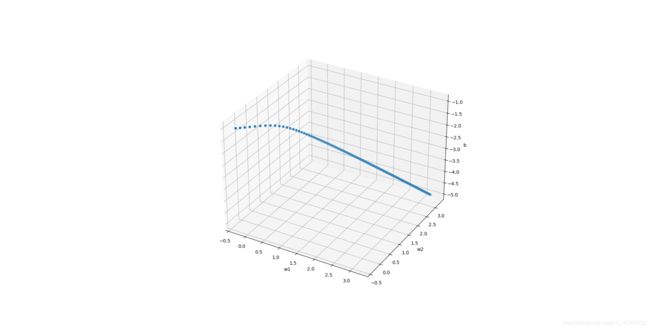
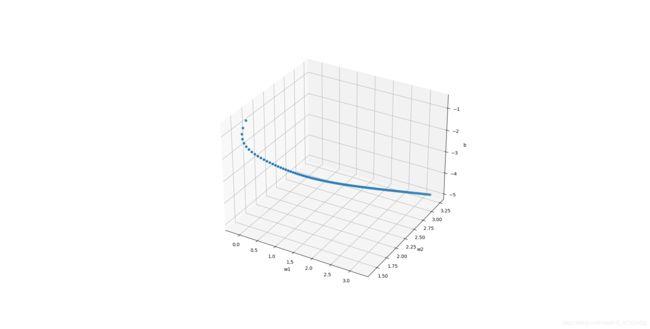
结果分析图:
以下三张散点图为三次与门的实验结果图,损失函数为MSE,学习速率为 1.0 1.0 1.0。
坐标轴分别为 w e i g h t 1 weight1 weight1、 w e i g h t 2 weight2 weight2、 b i a s bias bias,每一个点代表了 w e i g h t 1 + w e i g h t 2 + b i a s weight1 + weight2 + bias weight1+weight2+bias的值。
可以看到由于初始值为随机从正态分布中取出三个任意值,故三张图中虽然起点各不相同,但随着对模型训练次数的增加,点最终都取到了近乎相同的位置,且将三者的比例与作业二中给定的比例比较发现,近乎相同,表明训练较为成功。
知识框架
原理概述
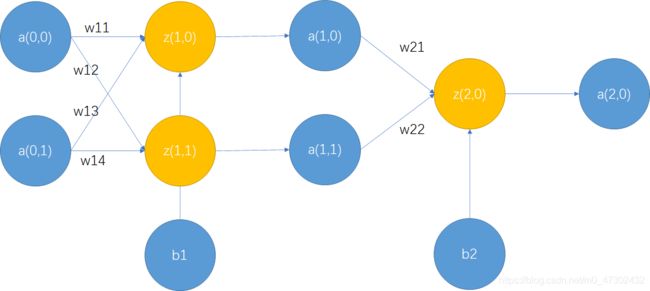
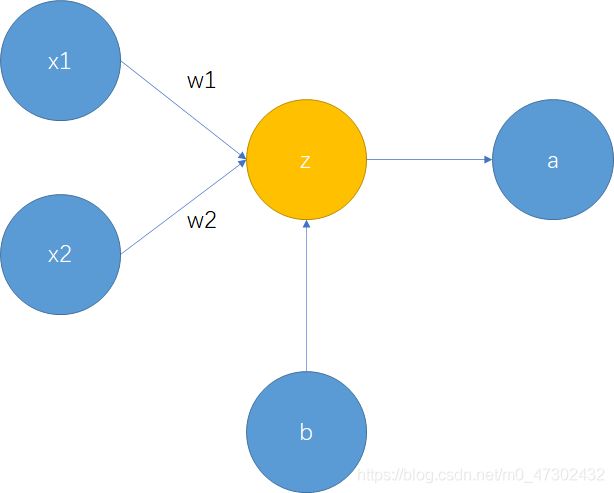
本例中同HW02一样,从四种里选取了较有代表性的与门和异或门来进行实现,其中与门的神经网络结构为两层,无隐含层;异或门的神经网络结构为三层,有一层含两个神经元的隐含层。图示结构如下:
与门:
异或门

以结构较为简单的与门举例,从HW02中,我们已经实现了在给定了一组权重后,程序通过这样的结构来输出,我们在前文中提出了这样的问题,这个给定的权重是我们进行了计算之后,人工取出的数值,而程序也只是像一个计算器一样,仅仅做了一些“计算”而已,似乎这里面并没有体现出什么“智能”。
那么依据我们的问题来看,似乎如果程序能够代替我们人工去计算出一组符合要求的权重,这样的话,似乎看起来会比较“智能”。
而这一次的作业便是在程序起始的时候,随机给定一组初始的权重值,本例中采取从正态分布中随机选取所需数量的值来作为初始权重,然后随着程序不断的推进,让程序“智能”地自行去将权重逐渐修正到符合需求的大小去。
损失函数
大多数深度学习算法都涉及某种形式的优化。
优化是指改变 x x x以最小化或最大化某个函数 f ( x ) f(x) f(x)的任务
通常以最小化 f ( x ) f(x) f(x)指代大多数优化问题,最大化可经由最小化算法最小化 − f ( x ) -f(x) −f(x)来实现。
将待优化的函数称为目标函数(objective function)
对其最小化时,称为损失函数(loss function)
通常使用上标*表示最小化或最大化函数的x值。
x ∗ = a r g m i n f ( x ) x^* = argminf(x) x∗=argminf(x)
——《深度学习》 - Ian Goodfellow 等
将随机事件或其有关随机变量的取值映射为非负实数以表示该随机事件的“风险”或“损失”的函数。
即当前模型与理想模型的差距。
——百度百科
那么具体到我们这个问题里也就是说,在我们随机指定了权重亦或者是在修正权重的时候,我们需要一个东西来帮助我们去衡量我们当前的权重是否“足够好”,若是不够好,那么我们应当朝着哪个方向如何去继续修正它。
本例中,我们选取了两种损失函数来去帮助我们完成权重的修正,MSE和CE。
MSE名为均方误差,原理理解起来较为简单直接,但其理论学习速度尤其是模型初始学习速度并不很如人意。
CE名为交叉熵,原理相较MSE理解起来较难,但其理论学习速率相较MSE更快一些。
MSE(Mean Square Error) 均方误差
l o s s = 1 N × ∑ i = 1 N ( y i − y i ^ ) 2 loss=\frac{1}{N}\times\sum_{i=1}^N{(y_i-\hat{y_i})}^2 loss=N1×i=1∑N(yi−yi^)2
其中 y y y代表我们模型的当前输出,而 y ^ \hat{y} y^代表模型的预期输出,或称之为正确输出。
那么这个损失函数的定义理解起来就较为容易了,即将所有的当前输出与预期输出作差后将其平方值相加取平均。
那么这个值越大就说明离目标越远。
那么为什么会说MSE在理论上来说,模型初始学习速度很慢呢?
这个原因主要在于我们选用的激活函数Sigmoid和MSE并不能很好的配合,在反向传播中,我们会需要去考虑 ∂ l o s s ∂ w \frac{\partial{loss}}{\partial{w}} ∂w∂loss的大小问题,至于原理和详细推导我们在下文中会详述,此处暂时先抛出一个结论:
∂ l o s s ∂ w 1 = [ 2 N × ∑ i = 1 N ( y i − y i ^ ) ] × y × ( 1 − y ) × x 1 \frac{\partial{loss}}{\partial{w_1}}=[\frac{2}{N}\times\sum_{i=1}^N{(y_i-\hat{y_i})}]\times y\times(1-y)\times x_1 ∂w1∂loss=[N2×i=1∑N(yi−yi^)]×y×(1−y)×x1
由公式可知,当 y y y的值在接近 0 0 0或 1 1 1时, ∂ l o s s ∂ w \frac{\partial{loss}}{\partial{w}} ∂w∂loss的值将会接近于 0 0 0,而 ∂ l o s s ∂ w \frac{\partial{loss}}{\partial{w}} ∂w∂loss的值与学习速度成正比,因此理论上来说,MSE + Sigmoid的组合将会使得模型一开始的速度很慢。
CE(Cross Entropy) 交叉熵
本节中关于交叉熵的讨论参考自CSDN博客:
一文搞懂交叉熵在机器学习中的使用,透彻理解交叉熵背后的直觉
首先抛出结论:
若某事件仅有两种结果,则有简化的 l o s s loss loss和 ∂ l o s s ∂ w \frac{\partial{loss}}{\partial{w}} ∂w∂loss:
l o s s = − y ^ × l n ( y ) − ( 1 − y ^ ) × l n ( 1 − y ) loss=-\hat{y}\times ln(y)-(1-\hat{y})\times ln(1-y) loss=−y^×ln(y)−(1−y^)×ln(1−y)
∂ l o s s ∂ w 1 = ( y − y ^ ) × x 1 \frac{\partial{loss}}{\partial{w_1}}=(y-\hat{y})\times x_1 ∂w1∂loss=(y−y^)×x1
可以看到,相较之于MSE而言,CE只会受到当前值与期望值的差值所影响,且差值越大, ∂ l o s s ∂ w \frac{\partial{loss}}{\partial{w}} ∂w∂loss也越大,那么学习速度也就越快,显然克服了MSE的问题。
那么,MSE的公式看起来似乎很容易理解,甚至它的名字,均方误差,听起来都很好理解,可是无论是交叉熵这个名字,还是说它的公式,似乎都很难直观的去看出来这个损失函数提出的原理,因此,我将在此,参考上文所述的那一篇博客,着重解释一下什么是交叉熵,以及它是如何推导出来的。
信息量
首先,我们给出一个新的概念,信息量。
举个简单的例子:
事件一:Doinb拿AP佐伊斩获五杀。
事件二:Doinb决胜局拿了卡尔玛璐璐。
那么显而易见,事件一的信息量要远大于事件二,因为事件二发生的概率很大,而事件一几乎不可能发生。那么当一件越不可能的事情发生了,我们获取到的信息量就越大。也就是说,事件发生的概率和其信息量的大小应该成反比。
假设 X X X是一个离散型随机变量,其概率分布函数为 p ( x ) p(x) p(x),那么我们定义事件 X = x 0 X=x_0 X=x0的信息量为:
I ( x 0 ) = − l n ( p ( x 0 ) ) I(x_0)=-ln(p(x_0)) I(x0)=−ln(p(x0))
熵
在本节的开始为使公式更为明了简单,故预设了前提为事件仅有两种结果,而在此处我们把可能性推广到两种以上,即假设有 n n n种可能性,则每一种可能性都有一个概率 p ( x i ) p(x_i) p(xi)。
举一个三种可能性的例子,FPX前打野BO的下场:
| 序号 | 事件 | 概率 p p p | 信息量 I I I |
|---|---|---|---|
| A | 终身禁赛 | 0.7 | − l n ( 0.7 ) = 0.36 -ln(0.7)=0.36 −ln(0.7)=0.36 |
| B | 禁赛三年 | 0.2 | − l n ( 0.2 ) = 1.61 -ln(0.2)=1.61 −ln(0.2)=1.61 |
| C | 原地复出还赶得上打季后赛 | 0.1 | − l n ( 0.1 ) = 2.30 -ln(0.1)=2.30 −ln(0.1)=2.30 |
熵用来表示所有信息量的期望。
H = − ∑ i = 1 n p ( x i ) × l n ( p ( x i ) ) H=-\sum_{i=1}^n{p(x_i)\times ln(p(x_i))} H=−∑i=1np(xi)×ln(p(xi))
= 0.7 × 0.36 + 0.2 × 1.61 + 0.1 × 2.30 \ \ \ \ \ =0.7\times 0.36+0.2\times 1.61+0.1\times 2.30 =0.7×0.36+0.2×1.61+0.1×2.30
= 0.804 \ \ \ \ \ =0.804 =0.804
相对熵(KL散度)
同一个随机变量 X X X有两个单独的概率分布 p ( x ) p(x) p(x)和 q ( x ) q(x) q(x),则用KL散度来衡量二者的差异。
通常用 p p p来表示真实分布,即预期输出 y ^ \hat{y} y^,用 q q q来表示预测分布,即模型当前输出 y y y。
D K L ( p ∣ ∣ q ) = ∑ i = 1 n p ( x i ) × l n ( p ( x i ) q ( x i ) ) D_{KL}(p||q)=\sum_{i=1}^n{p(x_i)}\times ln(\frac{p(x_i)}{q(x_i)}) DKL(p∣∣q)=i=1∑np(xi)×ln(q(xi)p(xi))
D K L D_{KL} DKL值越小,则 p p p分布和 q q q分布越接近。
交叉熵
D K L ( p ∣ ∣ q ) = ∑ i = 1 n p ( x i ) × l n ( p ( x i ) ) − ∑ i = 1 n p ( x i ) × l n ( q ( x i ) ) D_{KL}(p||q)=\sum_{i=1}^n{p(x_i)}\times ln(p(x_i))-\sum_{i=1}^n{p(x_i)}\times ln(q(x_i)) DKL(p∣∣q)=∑i=1np(xi)×ln(p(xi))−∑i=1np(xi)×ln(q(xi))
= − H ( p ( x ) ) + [ − ∑ i = 1 n p ( x i ) × l n ( q ( x i ) ) ] \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =-H(p(x))+[-\sum_{i=1}^n{p(x_i)}\times ln(q(x_i))] =−H(p(x))+[−∑i=1np(xi)×ln(q(xi))]
即 相对熵 = − p -p −p的熵 + 交叉熵
如上文所述,一般将 p p p用来表示真实分布 y ^ \hat{y} y^,故而其为一定值,因此 H ( p ( x ) ) H(p(x)) H(p(x))也为一常数,因此交叉熵即可用来直接反映真实分布和预测分布的差距。
Back-Propagation
本小节中将接着前面抛出的问题来进行详细讨论,即如何让程序看起来“很智能”地去从随机给定的起始参数开始,不断修正不断学习,最终成功找到一组适合的、符合要求的参数来完成一个模型的训练。
反向传播(Error Back Propagation)算法是我们学习人工智能时,会遇到的第一个显得“较为智能”的算法。它的核心问题便在于去解决神经网络中参数的求导问题,其原理源自多元函数的链式法则,它将会与梯度下降法相配合,从而完成网络的训练。
我们再把这一张图拿出来看一下,加入我们选取较为简单的MSE + Sigmoid这一损失函数和激活函数的组合来考虑这一不含隐含层的两层神经网络。
z = x 1 × w 1 + x 2 × w 2 + b z=x_1\times w_1+x_2\times w_2+b z=x1×w1+x2×w2+b
a = s i g m o i d ( z ) = 1 1 + e − z a=sigmoid(z)=\frac{1}{1+e^{-z}} a=sigmoid(z)=1+e−z1
l o s s = ( a − a ^ ) 2 loss=(a-\hat{a})^2 loss=(a−a^)2
由上文所述可知,损失函数的提出便是为了量化考虑我们的当前输出与预期输出之间的差距,而当我们固定输入值后,那么影响 l o s s loss loss值的因素便只剩下了参数 w e i g h t weight weight和 b i a s bias bias,此处我们选取更具有代表性的 w e i g h t weight weight来进行讨论。
由上式可知, w e i g h t weight weight先影响到了 z z z的值,再通过 z z z影响了 a a a的值,最后通过 a a a来计算出了 l o s s loss loss的值,因此,我们似乎可以通过导数的链式法则来去考虑 w e i g h t weight weight对 l o s s loss loss的影响。
∂ l o s s ∂ w 1 = ∂ l o s s ∂ a × ∂ a ∂ z × ∂ z ∂ w 1 \frac{\partial{loss}}{\partial{w_1}}=\frac{\partial{loss}}{\partial{a}}\times \frac{\partial{a}}{\partial{z}}\times \frac{\partial{z}}{\partial{w_1}} ∂w1∂loss=∂a∂loss×∂z∂a×∂w1∂z
而这拆开的三项又分别可以快速计算得出:
∂ z ∂ w 1 = x 1 \frac{\partial{z}}{\partial{w_1}}=x_1 ∂w1∂z=x1
∂ a ∂ z = a × ( 1 − a ) \frac{\partial{a}}{\partial{z}}=a\times(1-a) ∂z∂a=a×(1−a)
∂ l o s s ∂ a = 2 × ( a − a ^ ) \frac{\partial{loss}}{\partial{a}}=2\times(a-\hat{a}) ∂a∂loss=2×(a−a^)
由此便可计算出:
∂ l o s s ∂ w 1 = ∂ l o s s ∂ a × ∂ a ∂ z × ∂ z ∂ w 1 \frac{\partial{loss}}{\partial{w_1}}=\frac{\partial{loss}}{\partial{a}}\times \frac{\partial{a}}{\partial{z}}\times \frac{\partial{z}}{\partial{w_1}} ∂w1∂loss=∂a∂loss×∂z∂a×∂w1∂z
= 2 × ( a − a ^ ) × a × ( 1 − a ) × x 1 \ \ \ \ \ \ \ \ \ =2\times(a-\hat{a})\times a\times(1-a)\times x_1 =2×(a−a^)×a×(1−a)×x1
那么又产生一个新的问题, ∂ l o s s ∂ w \frac{\partial{loss}}{\partial{w}} ∂w∂loss又是如何去调整 l o s s loss loss,亦或者是将其调整到哪里算是合适呢?
Gradient Descent
我们知道,现在的目的是最小化我们的损失函数,举一个形象化的例子,我们作为一个伞兵,目的地是一座名为损失函数的高山中,它的山洼处最低点,但是这个任务艰巨的地方是什么呢,我们在跳伞前眼镜碎了,高度近视的我们,并不清楚这座山的全貌,以及到底山洼最低点在哪里,我们只能看到身边半径五米大小的环境,而超出五米的地方,俗称,“战争迷雾”。坏消息总是接踵而至,我们在下落的时候遇到了强风,所以我们的伞兵一号只知道自己在山上,却并不清楚自己到底在山的哪里。
那么伞兵一号应该如何去寻找自己的任务目标——山洼处最低点呢?
他环顾了一下自己能看到的半径五米大小的范围内,找到了一个较低的方向,朝着这个方向走了一步,然后不断重复这一过程,那么大概率来说,他最终会找到任务目标的。
在这个例子中,伞兵不知道自己所处的位置,就像我们随机给定的权重和偏置值的初始值,而我们如何去找一个所谓的“视野范围内”的较低位置的方向呢?
梯度,即 ▽ f ( x , y ) = { ∂ f ∂ x , ∂ f ∂ y } = f x ( x , y ) i ⃗ + f y ( x , y ) j ⃗ \bigtriangledown{f(x,y)}=\{\frac{\partial{f}}{\partial{x}},\frac{\partial{f}}{\partial{y}}\}=f_x(x,y)\vec{i}+f_y(x,y)\vec{j} ▽f(x,y)={∂x∂f,∂y∂f}=fx(x,y)i+fy(x,y)j,其表示函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。
而梯度下降法本质上其实也就是,通过一步步的迭代求解,得到最小化的损失函数以及模型参数值。
因此,假如我们给定一个人为设置的学习速率 η \eta η,也可以理解为步长,还拿伞兵的例子来形象化举例的话,就是他可以选择是走十步再停下来环顾四周重新确定方向,也可以只走五步就停下来环顾四周确定方向。那么这两种选择的优劣就在于,走十步的话,停下来找方向的次数就少,那么整体效率会高,但是可能在方向的选取上就不如只走五步的方向选取更加精确了。
类比于此,我们取梯度的负值作为每次更新的方向,于是我们可以得到这样的算式:
w i ∗ = w i − η × ∂ l o s s ∂ w i w_i^*=w_i-\eta\times\frac{\partial{loss}}{\partial{w_i}} wi∗=wi−η×∂wi∂loss
程序详解
程序的大体框架类似HW02的类及方法,同样是 t e s t . p y test.py test.py、 l o g i c _ g a t e s . p y logic\_gates.py logic_gates.py、 n e u r a l _ n e t w o r k . p y neural\_network.py neural_network.py。
在 l o g i c _ g a t e s . p y logic\_gates.py logic_gates.py定义的 c l a s s A N D class\ AND class AND和 c l a s s X O R class\ XOR class XOR中都加入了一个新的方法 t r a i n train train。
# class AND
def train(self):
print("\nStarting training Network for AND Gate")
# 创建训练用的数据集
dataset = torch.FloatTensor([[0, 0], [0, 1], [1, 0], [1, 1]])
# 创建用来存储目标结果的4*1大小的张量
target_data = torch.zeros((len(dataset), 1), dtype=torch.int)
# 使用数据集对模型进行反复训练
for i in range(self.max_iter):
# 打乱原始数据集的顺序以生成多组训练数据
indices = torch.randperm(4)
train_data = torch.index_select(dataset, 0, indices)
# 找到训练数据对应的目标结果
for j in range(len(dataset)):
target_data[j] = train_data[j, 0] and train_data[j, 1]
# 开始训练
if self.and_gate.total_loss > 0.01: # 若total_loss比0.01大则继续训练
output = self.and_gate.forward(train_data) # 进行正向过程(Forward pass)以得到各层的输入元素 即(偏z/偏w)
# 此处可选择 MSE CE 损失函数
self.and_gate.backward(target_data, "MSE") # 进行反向过程(Backward pass)以得到(偏loss/偏w)
self.and_gate.updateParams(0.5) # 更新权重张量 learning_rate设置为1
else:
print("Training completed in %d iterations\n" % i)
break # 此时表示total_loss已经小于0.01 可以跳出循环了
old_weights = torch.FloatTensor([[-30, 20, 20]])
new_weights = self.and_gate.getLayer(0)
print("Manually set Weights: %r\n Newly learned Weights %r\n" % (old_weights, new_weights))
对于与门来说,总共只有四种输入,故设置数据集 d a t a s e t dataset dataset为torch.FloatTensor([[0, 0], [0, 1], [1, 0], [1, 1]])。
通过torch.randperm(n)和torch.index_select(input, dim, indices)来从数据集中随机创建训练集。
torch.randperm(n)->Tensor 将返回一个从 0 0 0到 n − 1 n-1 n−1的整数的随机排列张量。
torch.index_select(input, dim, indices)->Tensor 将返回一个与原张量不共享内存的新张量,新张量将沿着 d i m dim dim维度,以 i n d i c e s indices indices的序列重新组合的 i n p u t input input张量。
eg:
>>> x = torch.tensor([[0.1, 0.02, -0.5, -1.0],
[-0.4, 0.2, -0.1, -1.1],
[-1.1, -0.6, 0.7, -0.6]])
>>> indices = torch.tensor([0, 2])
>>> torch.index_select(x, 0, indices)
tensor([[ 0.1000, 0.0200, -0.5000, -1.0000],
[-1.1000, -0.6000, 0.7000, -0.6000]])
>>> torch.index_select(x, 1, indices)
tensor([[ 0.1000, -0.5000],
[-0.4000, -0.1000],
[-1.1000, 0.7000]])
在创建好训练集后,再用and直接算出当前训练集的正确结果:
for j in range(len(dataset)):
target_data[j] = train_data[j, 0] and train_data[j, 1]
这样生成的训练集将会在每一次循环中为算法输入四组数据以训练模型,如图所示:

一般而言,我们将整个过程分为两部分,第一部分为前向传播,第二部分则为反向传播。
前向传播的目的在于通过我们输入的训练集数据以及此时的 w e i g h t weight weight和 b i a s bias bias来计算出本次训练时神经网络中的各项数据,例如激活函数的输入和输出的 z z z数组和 a a a数组。
通过前向传播将所有的数据计算出之后,我们接下来就要通过反向传播来计算我们的 ∂ l o s s ∂ w i \frac{\partial{loss}}{\partial{w_i}} ∂wi∂loss。
我们假定损失函数 L o s s f u n c t i o n Loss\ function Loss function为 l o s s = f ( a ) loss=f(a) loss=f(a),激活函数 A c t i v a t i o n F u n c t i o n Activation\ Function Activation Function为 a = g ( z ) a=g(z) a=g(z)。
∂ l o s s ∂ w 1 = ∂ l o s s ∂ a × ∂ a ∂ z × ∂ z ∂ w 1 \frac{\partial{loss}}{\partial{w_1}}=\frac{\partial{loss}}{\partial{a}}\times \frac{\partial{a}}{\partial{z}}\times \frac{\partial{z}}{\partial{w_1}} ∂w1∂loss=∂a∂loss×∂z∂a×∂w1∂z
= f ′ ( a ) × g ′ ( z ) × x 1 \ \ \ \ \ \ \ \ \ =f^{'}{(a)}\times g^{'}{(z)}\times x_1 =f′(a)×g′(z)×x1
从上式可以看出,组成 ∂ l o s s ∂ w i \frac{\partial{loss}}{\partial{w_i}} ∂wi∂loss的三部分中,前两部分都和我们选取的损失函数和激活函数相关,而第三项则是与输入元素相关的。而输入元素是可以在前向传播中得到的,剩下的两项则是需要从反向传播中再求出来的。
前向传播
前向传播的内容事实上就是HW02的内容,按照神经网络的结构自输入层开始计算,将所有所需的数据顺序计算出来即可。
在本程序中,第 i i i层的输入数据来自 a [ i ] a[i] a[i],其与权重数组相乘后得到的值存放进 z [ i + 1 ] z[i+1] z[i+1]内,再将 z [ i + 1 ] z[i+1] z[i+1]作为激活函数的自变量送入自变量中,得到输出值 a [ i + 1 ] a[i+1] a[i+1]来作为本层的输出与下一层的输入。
反向传播
在上文的讨论中,我们举的例子是一个较为简单的两层神经网络,且输入为两个神经元输出为一个神经元。那么在这个地方,我们将会考虑一些更复杂的情况。
c a s e 2 case\ 2 case 2

对于 c a s e 1 case\ 1 case 1来说,我们需要讨论的是以前面所述的模型为基础下,再加一层隐含层的话 ∂ l o s s ∂ w 11 \frac{\partial{loss}}{\partial{w_{11}}} ∂w11∂loss的值。
∂ l o s s ∂ w 11 = ∂ z ( 1 , 0 ) ∂ w 11 × ∂ a ( 1 , 0 ) ∂ z ( 1 , 0 ) × ∂ z ( 2 , 0 ) ∂ a ( 1 , 0 ) × ∂ a ( 2 , 0 ) ∂ z ( 2 , 0 ) × ∂ l o s s ∂ a ( 2 , 0 ) \frac{\partial{loss}}{\partial{w_{11}}}=\frac{\partial{z_{(1,0)}}}{\partial{w_{11}}}\times \frac{\partial{a_{(1,0)}}}{\partial{z_{(1,0)}}}\times \frac{\partial{z_{(2,0)}}}{\partial{a_{(1,0)}}}\times \frac{\partial{a_{(2,0)}}}{\partial{z_{(2,0)}}}\times \frac{\partial{loss}}{\partial{a_{(2,0)}}} ∂w11∂loss=∂w11∂z(1,0)×∂z(1,0)∂a(1,0)×∂a(1,0)∂z(2,0)×∂z(2,0)∂a(2,0)×∂a(2,0)∂loss
= [ ∂ z ( 1 , 0 ) ∂ w 11 ] × [ ∂ a ( 1 , 0 ) ∂ z ( 1 , 0 ) ] × [ ∂ z ( 2 , 0 ) ∂ a ( 1 , 0 ) ] × [ ∂ a ( 2 , 0 ) ∂ z ( 2 , 0 ) × ∂ l o s s ∂ a ( 2 , 0 ) ] \ \ \ \ \ \ \ \ \ =[\frac{\partial{z_{(1,0)}}}{\partial{w_{11}}}]\times [\frac{\partial{a_{(1,0)}}}{\partial{z_{(1,0)}}}]\times [\frac{\partial{z_{(2,0)}}}{\partial{a_{(1,0)}}}]\times [\frac{\partial{a_{(2,0)}}}{\partial{z_{(2,0)}}}\times \frac{\partial{loss}}{\partial{a_{(2,0)}}}] =[∂w11∂z(1,0)]×[∂z(1,0)∂a(1,0)]×[∂a(1,0)∂z(2,0)]×[∂z(2,0)∂a(2,0)×∂a(2,0)∂loss]
= a ( 0 , 0 ) × g ′ ( z ( 1 , 0 ) ) × w 21 × ∂ l o s s ∂ z ( 2 , 0 ) \ \ \ \ \ \ \ \ \ =a_{(0,0)}\times g^{'}{(z_{(1,0)})}\times w_{21}\times \frac{\partial{loss}}{\partial{z_{(2,0)}}} =a(0,0)×g′(z(1,0))×w21×∂z(2,0)∂loss
= a ( 0 , 0 ) × [ g ′ ( z ( 1 , 0 ) ) × w 21 × ∂ l o s s ∂ z ( 2 , 0 ) ] \ \ \ \ \ \ \ \ \ =a_{(0,0)}\times [g^{'}{(z_{(1,0)})}\times w_{21}\times \frac{\partial{loss}}{\partial{z_{(2,0)}}}] =a(0,0)×[g′(z(1,0))×w21×∂z(2,0)∂loss]
= a ( 0 , 0 ) × ∂ l o s s ∂ z ( 1 , 0 ) \ \ \ \ \ \ \ \ \ =a_{(0,0)}\times \frac{\partial{loss}}{\partial{z_{(1,0)}}} =a(0,0)×∂z(1,0)∂loss
由此算式推导可知,对于含多个隐含层的神经网络来说,事实上只需要多次迭代计算 ∂ l o s s ∂ z \frac{\partial{loss}}{\partial{z}} ∂z∂loss即可。
那么,据此结论来讨论 c a s e 2 case\ 2 case 2,对于多隐含层的神经网络,考虑其中第 i i i层开始的一层,假设已迭代知 ∂ l o s s ∂ z ( i + 2 , 0 ) \frac{\partial{loss}}{\partial{z_{(i+2,0)}}} ∂z(i+2,0)∂loss和 ∂ l o s s ∂ z ( i + 2 , 1 ) \frac{\partial{loss}}{\partial{z_{(i+2,1)}}} ∂z(i+2,1)∂loss,那么来尝试推导 ∂ l o s s ∂ w 11 \frac{\partial{loss}}{\partial{w_{11}}} ∂w11∂loss。
∂ l o s s ∂ w 11 = ∂ z ( i + 1 , 0 ) ∂ w 11 × ∂ a ( i + 1 , 0 ) ∂ z ( i + 1 , 0 ) × ∂ l o s s ∂ a ( i + 1 , 0 ) \frac{\partial{loss}}{\partial{w_{11}}}=\frac{\partial{z_{(i+1,0)}}}{\partial{w_{11}}}\times \frac{\partial{a_{(i+1,0)}}}{\partial{z_{(i+1,0)}}}\times \frac{\partial{loss}}{\partial{a_{(i+1,0)}}} ∂w11∂loss=∂w11∂z(i+1,0)×∂z(i+1,0)∂a(i+1,0)×∂a(i+1,0)∂loss
= ∂ z ( i + 1 , 0 ) ∂ w 11 × ∂ a ( i + 1 , 0 ) ∂ z ( i + 1 , 0 ) × ( ∂ z ( i + 2 , 0 ) ∂ a ( i + 1 , 0 ) × ∂ l o s s ∂ z ( i + 2 , 0 ) + ∂ z ( i + 2 , 1 ) ∂ a ( i + 1 , 0 ) × ∂ l o s s ∂ z ( i + 2 , 1 ) ) \ \ \ \ \ \ \ \ \ =\frac{\partial{z_{(i+1,0)}}}{\partial{w_{11}}}\times \frac{\partial{a_{(i+1,0)}}}{\partial{z_{(i+1,0)}}}\times(\frac{\partial{z_{(i+2,0)}}}{\partial{a_{(i+1,0)}}}\times \frac{\partial{loss}}{\partial{z_{(i+2,0)}}}+\frac{\partial{z_{(i+2,1)}}}{\partial{a_{(i+1,0)}}}\times \frac{\partial{loss}}{\partial{z_{(i+2,1)}}}) =∂w11∂z(i+1,0)×∂z(i+1,0)∂a(i+1,0)×(∂a(i+1,0)∂z(i+2,0)×∂z(i+2,0)∂loss+∂a(i+1,0)∂z(i+2,1)×∂z(i+2,1)∂loss)
= a ( i , 0 ) × g ′ ( z ( i + 1 , 0 ) ) × ( w 21 × ∂ l o s s ∂ z ( i + 2 , 0 ) + w 22 × ∂ l o s s ∂ z ( i + 2 , 1 ) ) \ \ \ \ \ \ \ \ \ =a_{(i,0)}\times g^{'}{(z_{(i+1,0)})}\times (w_{21}\times \frac{\partial{loss}}{\partial{z_{(i+2,0)}}}+w_{22}\times \frac{\partial{loss}}{\partial{z_{(i+2,1)}}}) =a(i,0)×g′(z(i+1,0))×(w21×∂z(i+2,0)∂loss+w22×∂z(i+2,1)∂loss)
虽然 c a s e 2 case\ 2 case 2中情况与本次作业无关,但我认为多分支的情况在以后的实际运用中应该是较为常见的,故而也将推导放在了这里,事实上,本例中仅异或门作为三层神经网络需要使用 c a s e 1 case\ 1 case 1外,其他并不需要考虑十分复杂的情况。
总结
本次作业中,实现了手动编写一个完整的反向传播算法,并且分别尝试了在激活函数为Sigmoid时,损失函数为MSE和CE两种情况下的学习模型。
虽然理论上CE效果较好,但可能是因为模型较为简单加之学习速率 η \eta η的选取数量较少,所以并未明显感到MSE效果不如CE,反而在学习速率 η \eta η的值为1.0的时候,CE反而无法在预定最大迭代次数(100000)内完成训练,反倒是MSE能够较好的完成训练。
(PS. 由于CE的代码是完全自己编写的,所以不排除是因为其实代码是写错了所以效果并不理想的原因……)
Still,通过本次作业,至少在MSE模块下,完整手动实现了反向传播算法的全部过程,对这一算法有了更深入的理解。