数据结构(7)-队列

定义

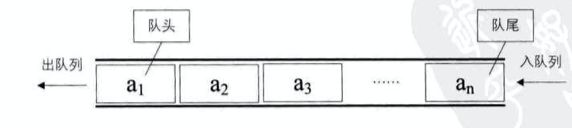
队列(Queue)是只允许在一端进行插入操作，在另一端进行删除操作的线性表。

队列是一种先进先出(First In First Out)的线性表，也就是FIFO。一般插入的一端称为队尾，删除的一端称为队头。

队列定义.png

队列的抽象数据类型

ADT 队列(Queue)

Data

和线性表相同。元素都具有相同的类型，相邻的元素具有前驱和后继关系。

Operation操作

InitQueue(*Q)：初始化，创建一个空队列
DestoryQueue(*Q)：销毁队列
ClearQueue(*Q)：清空队列
QueueIsEmpty(Q)：判断是否是空队列
QueueLenth(Q)：获取队列的长度
GetQueueHeadElement(Q, *e)：获取队列队头元素
EnQueue(*Q, e)：进入队列，称为队尾元素
DeQueue(*Q, *e)：出队列，删除队头元素

endADT

队列的存储结构

由于队列也是线性表，那么队列的存储结构也可以分为顺序存储和链式存储。

顺序结构队列

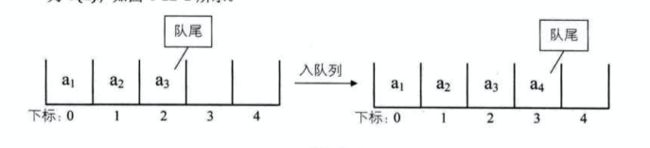
我们假设一个队列有n个元素，则顺序存储的队列需要创建一个大于n的数组，并把所有的元素都放在前n个位置，其中下标为0的是队头，下标为n的是队尾。当我们需要插入一个元素，也就是入队列：

顺序队列入队.png

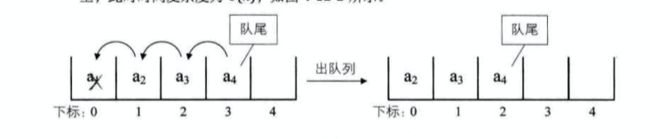
当我们需要删除一个元素，也就是队头出队列：

顺序队列出队.png

可以看出，这个实现就和线性表的顺序存储基本上一模一样，只是插入和删除的位置比较固定而已，此处就不多做赘述了。详见数据结构(2)-线性表之顺序存储。

可以看出队列出队的时间复杂度就是O(n)，如果不去限制队列的元素必须存储在数组的前n个单元这一条件，出队的性能就会大大增加。也就是说，队头不需要一定在下标为0的位置。

顺序队列不移动出队.png

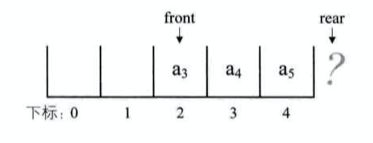
为了避免当只有一个元素时，队头和队尾重合使处理变得麻烦，所以引入两个指针，front指针指向队头元素，rear指针指向队尾元素的下一个位置，这样当front等于rear时，此队列不是还剩一个元素，而是空队列。

但是这种情况下，如果队尾满了，而队头由于出队移动了队列的中间，虽然此时总数并没有达到队列的最大值，但如果接着入队的话，因数组末尾元素已经占用，再向后加，就会产生数组越界的错误。我们把这种现象叫做“假溢出”。

队列溢出.png

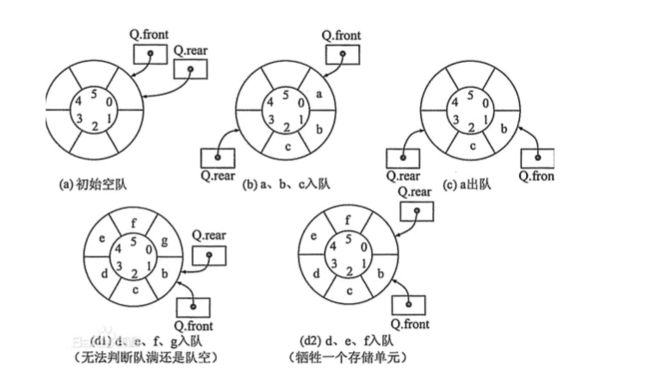
循环队列

为了解决队列假溢出的问题，我们可以让队列头尾相接，这样前面空出来的位置也可以接着使用了。这种头尾相接的顺序存储结构称为循环队列。

循环队列.png

可以看出，循环队列解决了队列假溢出的问题，但是却带来了另一个问题，就是无法判断队列是队满还是队空。之前我们说过，队列的front指针和rear指针相等的时候，是为队空，而此时队满的情况下，front指针和rear指针也是相等的。

那么如何解决这个问题呢?一种方式是单独使用一个变量来标志队满和队空；第二种方式就是我们修改队满的条件，保留一个元素空间，也就是让队列在还剩一个空间的时候就认为它是队满状态。此时队满的条件就是(rear + 1)%QueueSize == front。队列长度的计算公式为(rear - front + QueueSize) % QueueSize。

理清楚这些逻辑，我们再来看看循环队列的具体实现。

初始化循环队列

#define T_MAX_SIZE 100
#define T_ERROR -1
#define T_OK 1
typedef int TStatus;
typedef int ElementType;

typedef struct SeqQueue {
    ElementType data[T_MAX_SIZE]; // 申请内存
    int front;  // 队头指针
    int rear;   // 队尾指针
}SeqQueue;


TStatus InitSeqQueue(SeqQueue *Q) {
    Q->front = 0;
    Q->rear = 0
    
    return T_OK;
}

清空队列

顺序存储的队列清空只需要将front和rear赋值为0即可。

TStatus ClearQueue(SeqQueue *Q) {
    Q->front = 0;
    Q->rear = 0;
    return T_OK;
}

队列判空

front等于rear即为空队列。

bool QueueIsEmpty(SeqQueue Q) {
    if (Q.front == Q.rear) {
        return true;
    }
    return false;
}

获取队列长度

顺序存储的队列长度计算公式为(rear - front + QueueSize) % QueueSize。

int GetQueueLenth(SeqQueue Q) {
    return (Q.rear - Q.front + T_MAX_SIZE) % T_MAX_SIZE;
}

获取队列队头元素

TStatus GetQueueHeadElement(SeqQueue Q, ElementType *e) {
    if (Q.front == Q.rear) {
        return T_ERROR;
    }
    *e = Q.data[Q.front];
    return T_OK;
}

入队

如果队列不是队满，即可入队。入队的位置就在rear指针指向的位置。我们还需要移动rear指针的指向。

TStatus EnQueue(SeqQueue *Q, ElementType e) {
    if (Q == NULL) {
        return T_ERROR;
    }
    if ((Q->rear + 1) % T_MAX_SIZE == Q->front) {
        return T_ERROR;
    }
    Q->data[Q->rear] = e;
    Q->rear = (Q->rear + 1) % T_MAX_SIZE;
    
    return T_OK;
}

出队

如果队列不是队空，即可出队。出队的元素就在front指针指向的元素。另外还需要移动front指针的指向。

TStatus DeQueue(SeqQueue *Q, ElementType *e) {
    if (Q->front == Q->rear) {
        return T_ERROR;
    }
    *e = Q->data[Q->front];
    Q->front = (Q->front + 1) % T_MAX_SIZE;
    return T_OK;
}

链式结构队列

队列的链式存储结构，其实就是线性表的单链表，只不过它只能尾进头出而已。一般情况下，我们将front指针指向链表的头结点，而将rear指针指向链表尾部的结点。

链式队列示意图.png

下面，我们来看看链式队列的具体实现。

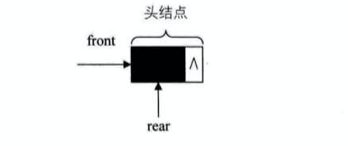
初始化链式队列

初始化链式队列的时候，队列只有一个头结点，此时front指针和rear指针都指向头结点。

链式空队列.png

typedef struct QueueNode {
    ElementType data;
    struct QueueNode *next;
}QueueNode, * LinkQueueNode;

typedef struct LinkQueue {
    LinkQueueNode front;   // 队头
    LinkQueueNode rear;    // 队尾
    int count;             // 队列长度
}LinkQueue;


TStatus InitLinkQueue(LinkQueue *Q) {
    // 初始化头结点 front和rear都指向头结点
    Q->front = Q->rear = (LinkQueueNode)malloc(sizeof(QueueNode));
    if (Q->front == NULL || Q->rear == NULL) {
        return T_ERROR;
    }
    Q->front->next = NULL;
    Q->count = 0;
    
    return T_OK;
}

清空链式队列

清空链式队列需要将队列中的结点全部都释放。

TStatus ClearLinkQueue(LinkQueue *Q) {
    LinkQueueNode p = Q->front->next;
    LinkQueueNode q;
    while (p) {
        q = p;
        free(p);
        p = q->next;
    }
    
    Q->front = Q->rear;
    Q->count = 0;
    
    return T_OK;
}

获取链式队列队头元素

TStatus GetLinkQueueHeadElement(LinkQueue Q, ElementType *e) {
    if (Q.front == Q.rear) {
        return T_ERROR;
    }
    *e = Q.front->next->data;
    return T_OK;
}

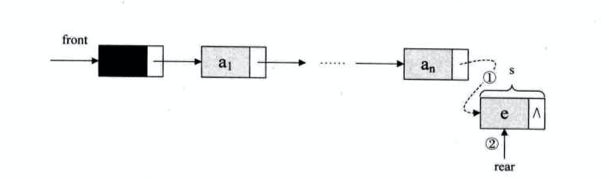
链式队列入队

链式队列入队需要注意的是插入的是链表的尾部，插入完成之后，我们需要将rear指针向后挪动一个位置，也就是让其指向新插入的元素。

链式队列入队.png

TStatus EnQueue(LinkQueue *Q, ElementType e) {
    if (Q == NULL) {
        return T_ERROR;
    }
    LinkQueueNode p = (LinkQueueNode)malloc(sizeof(QueueNode));
    if (p == NULL) {
        return T_ERROR;
    }
    p->next = NULL;
    p->data = e;
    // 插入链表
    Q->rear->next = p;
    // 修改rear指针指向
    Q->rear = p;
    Q->count += 1;
    
    return T_OK;
}

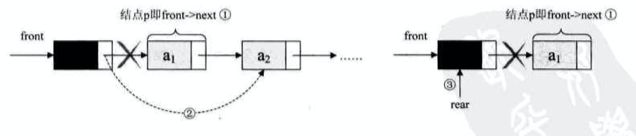
链式队列出队

链式队列出队，出的是链表表头的位置，也就是首元结点，我们需要修改头结点的指向。

链式队列出队.png

TStatus DeQueue(LinkQueue *Q, ElementType *e) {
    if (Q->front == Q->rear) {
        return T_ERROR;
    }
    LinkQueueNode p = Q->front->next;
    *e = p->data;

    // 头结点指向原来首元结点的下一个位置
    Q->front->next = p->next;
    free(p);
    Q->count -= 1;
    
    return T_OK;
}

总结

时间复杂度都为O(1)。但是链式队列在入队或者出队伴随有申请内存空间、释放内存空间的动作，还是有细微的差异。
空间复杂度上，循环队列必须预先申请固定长度的内存空间，可能存在浪费的情况。虽然链式空间每个结点都多了一个指针域，但是相比循环链表要更加灵活。

一般情况下，在已知队列最大长度的时候可以使用循环队列，反之则建议使用链式队列。