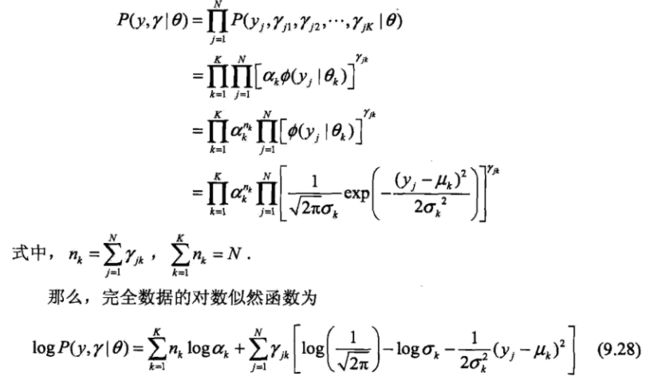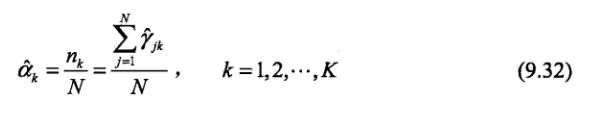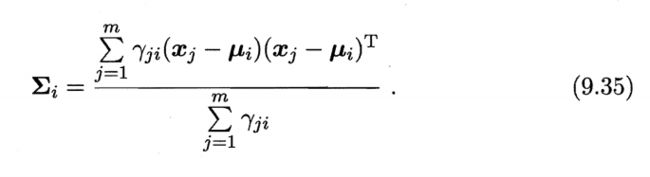定义
EM算法的一个重要应用是高斯混合模型的参数估计,高斯混合模型的应用广泛,在许多情况下,EM算法是学习高斯混合模型的有效手段。高斯混合模型是由多个高斯模型线性组合成的,所以可以构成很复杂的概率密度函数,可以无限逼近任何连续的概率密度函数。
高斯混合模型理论
下面看一下高斯混合模型EM算法的理论(出自《统计学习方法》和西瓜书《机器学习》)。
求极大值的思想:
(1)改变一个变量,固定其他变量。
(2)改变的变量使似然函数达到极大值,则固定该变量。选择另外一个变量重复步骤(1),直到似然函数收敛,则算法结束。
下面就推导一下,更新参数的计算公式。
高斯混合模型的参数估计EM算法完整流程
完整代码
import numpy as np
from numpy import *
import matplotlib.pyplot as plt
import math
def get_set_data(file_name):
fd = open(file_name)
set_data = []
for line in fd.readlines():
line_data = line.strip().split()
set_data.append([float(line_data[0]), float(line_data[1])])
return set_data
def gaussion_distribution(x, miu, sigma):
n = shape(x)[1]
sigma_mat = mat(sigma)
expOn = float(-0.5*(x - miu)*(sigma_mat.I)*((x - miu).T))
divBy = pow(2*pi, n/2)*pow(linalg.det(sigma_mat), 0.5)
return pow(e, expOn)/divBy
def gaussion_em(data_in, alpha, miu, sigma, iterator_num):
K = shape(alpha)[1]
N,n = shape(data_in)
gama = mat(zeros((K, N)))
temp_value = mat(zeros((K, N)))
for s in range(iterator_num): #迭代iterator_num次
for j in range(N):
for k in range(K):
temp_value[k, j] = alpha[:, k] * gaussion_distribution(data_in[j, :], miu[k], sigma[k])
for j in range(N):
sum = 0
for k in range(K):
sum += temp_value[k, j]
for k in range(K):
gama[k, j] = temp_value[k, j] / sum
for k in range(K):
sum = mat(zeros((1, n)))
sum2 = mat(zeros((n, n)))
sum1 = 0
for j in range(N):
sum[0, :] += gama[k, j] * data_in[j, :]
sum1 += gama[k, j]
miu[k] = sum[0, :] / sum1
for j in range(N):
sum2 += gama[k, j] * (data_in[j, :] - miu[k]).T * (data_in[j, :] - miu[k])
sigma[k] = sum2 / sum1
alpha[:, k] = sum1 / N
return alpha,miu,sigma,gama
def get_classify(gama):
label = 0
K,N = shape(gama)
labels = mat(zeros((N, 1)))
for i in range(N):
index_max = argmax(gama[:, i]) #计算每一个观测变量最有可能属于第几个高斯分量
labels[i, 0] = index_max
return labels
def show_experiment_plot(data_mat, labels):
N = shape(data_mat)[0]
for i in range(N):
if(labels[i, 0] == 0):
plt.plot(data_mat[i, 0], data_mat[i, 1], "ob")
elif(labels[i, 0] == 1):
plt.plot(data_mat[i, 0], data_mat[i, 1], "or")
else:
plt.plot(data_mat[i, 0], data_mat[i, 1], "og")
plt.xlabel("X")
plt.ylabel("Y")
plt.show()
if __name__ == "__main__":
set_data = get_set_data("set_data.txt")
alpha_mat = mat([1/3, 1/3, 1/3])
data_mat = mat(set_data)
miu_mat = [data_mat[5, :], data_mat[21, :], data_mat[26, :]]
sigma_mat = [mat([[0.1, 0], [0, 0.1]]) for x in range(3)]
#print(data_mat)
alpha,miu,sigma,gama = gaussion_em(data_mat, alpha_mat, miu_mat, sigma_mat, 50)
print("alpha = ", alpha)
print("\n")
print("miu = ", miu)
print("\n")
print("sigma = ", sigma)
print("\n")
print("gama = ", gama)
print("\n")
labels = get_classify(gama)
show_experiment_plot(data_mat, labels)
本文的初始化参数、输入数据采用的是《机器学习》上的。
输入数据:
0.697 0.460
0.774 0.376
0.634 0.264
0.608 0.318
0.556 0.215
0.403 0.237
0.481 0.149
0.437 0.211
0.666 0.091
0.243 0.267
0.245 0.057
0.343 0.099
0.639 0.161
0.657 0.198
0.360 0.370
0.593 0.042
0.719 0.103
0.359 0.188
0.339 0.241
0.282 0.257
0.748 0.232
0.714 0.346
0.483 0.312
0.478 0.437
0.525 0.369
0.751 0.489
0.532 0.472
0.473 0.376
0.725 0.445
0.446 0.459
初始化参数:
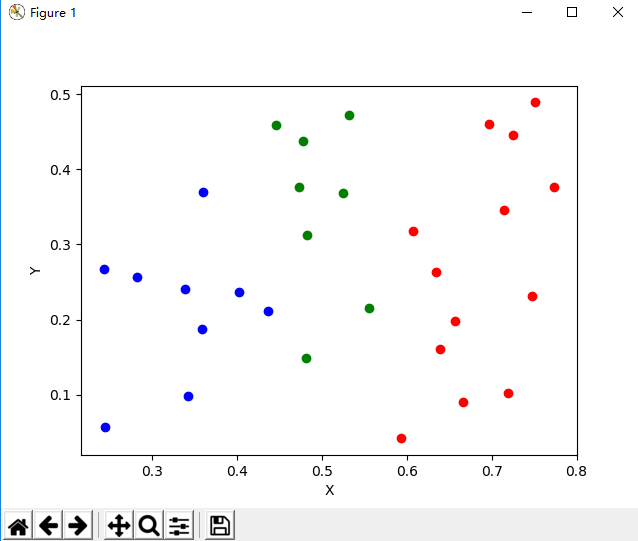
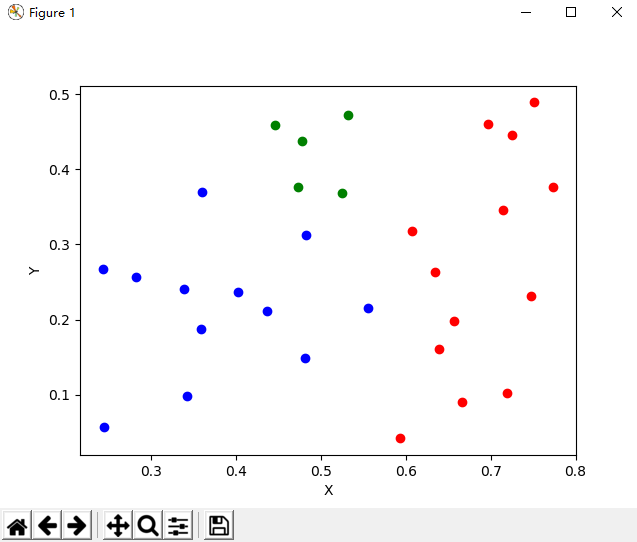
实验结果
迭代50次效果图
《机器学习》上的实验结果
两者对比同样迭代50次的时候,结果是一样的,算法正确。
我们可以改变一下迭代次数,看一下效果图。
迭代100次效果图
迭代150次效果图
发现迭代迭代50次和迭代100次的效果图是不一样的,100次和150次迭代的效果图是一样的。说明该算法在迭代次数50~100次之间就已经收敛了。