探索《小数的性质》(四下)
前言
在生活中,学生和小数已有很亲密的接触,常见的商品标价牌上有规范的两位小数的记法(比如3.20元),也有简单的记法(比如3.2元),学生从这些现象中对小数的性质已经有了一定的感悟,但也仅仅是初步的体验。
本节课是针对小数性质的本质进行系统的学习。
一、比较、发现
出示例1:比较0.1m、0.10m和0.100m的大小,你发现了什么?
学生观察米尺,在米尺中找出0.1m ,0.10m和0.100m。(边回答边课件演示)
师:(课件截取米尺中的有效部分,引导学生观察)从中你发现了什么?它们的大小怎样?
生:从米尺我发现0.1m,0.10m和0.100m都是指米尺上同一段的长度,所以
0.1m=0.10m=0.100m。
师:(对三个小数重点标红,引导学生观察。)观察这三个小数,从左往右看,小数的末尾有什么变化?小数的大小有什么变化?
生:小数的末尾添上一个0、两个0,但是它们的大小不变。
师:从右往左看,小数的末尾有什么变化?小数的大小有什么变化?
生:小数的末尾去掉了一个0、两个0,它 们的大小不变。
师:综合两种情况,你又从中发现什么?(交流讨论)
生汇报:小数的末尾添上0或去掉0,小数的大小不变。
师:是不是所有的小数都具有这样的特点呢?今天我们就来深入探究这个问题。
设计意图:让学生在熟悉的米尺中找出这三段长度,通过观察,引导讨论,让学生自己发现规律,初步感知小数的性质。
二、从生活情境引发思考
师:昨天,老师在发微信红包的时候,无意中发现这么一个问题:
课件出示:
师:我想发“0.3”元,可是输入以后,系统显示的实时金额却是“0.30元”。咦,你们觉得这两个钱数相等吗?为什么?
生:相等。因为0.3元是3角,0.30元也是3角。
师:结合单位比较,我们发现这两个小数是相等的。那我们还能怎样更直观地验证0.3和0.30这两个小数是相等的呢?
设计意图:利用孩子们都具有的生活常识,进一步激发学生的探索欲,让学生再一次感悟到小数末尾添0去0,小数的大小数不变的。
三、操作、观察,探究规律
为了便于研究,我给学生提供了一下几种研究方式:
A、借助图形
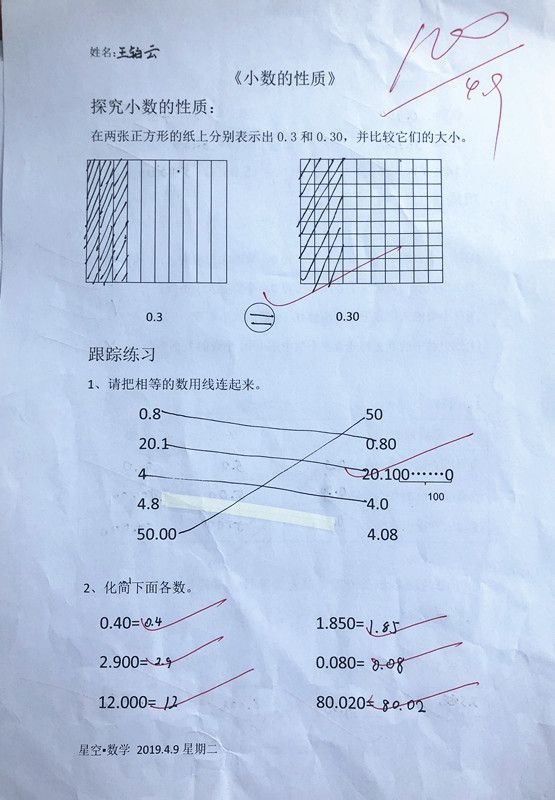
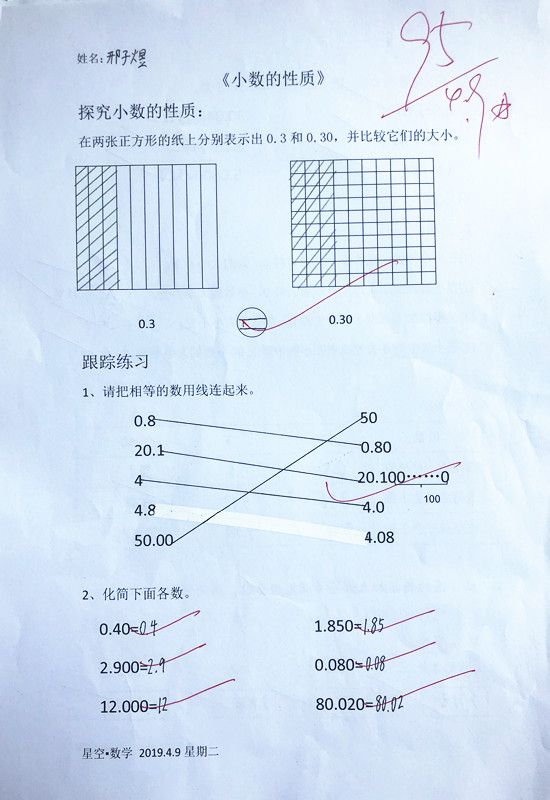
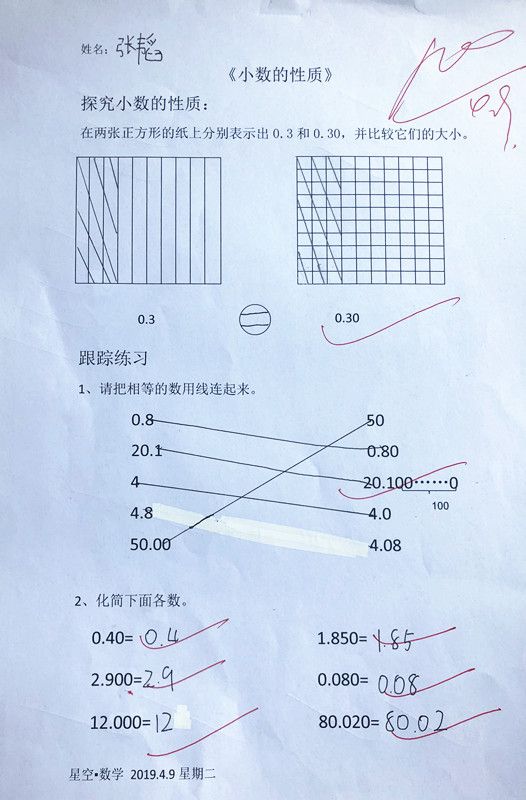
师:现在有两个大小相等的正方形,请在图中分别表示出0.3和0.30。并比较涂色部分的大小,你发现了什么?
师:你是怎样画的?你为什么这样画?
生:在学习小数的意义时我们知道一位小数表示十分之几,所以0.3就是十分之三,表示将正方形平均分成10份,取其中的3份。
追问:因此,0.3的计数单位是?
全班齐答:0.1
生:0.30表示百分之三十,就是将正方形平均分成100份,取其中的30份。(学生回答,课件演示)
师:那么,0.30的计数单位是?
全班齐答:0.01
想一想:什么变了?什么没变?你发现了什么规律?用给自己的话把发现的规律告诉大家。(先让学生自由发表看法,教师再进行小结)
小结:小数的大小不变,但意义和计数单位变了。
设计意图:通过直观图示,让学生更清晰认识到小数性质的本质中变与不变的量。
B、借助数位表
师:观察这个等式,0.3 = 0.30 ,照这样继续想下去,你还能想到哪些数与它相等?
生:可能它们还和 0.300 相等……
师:这样写下去能写得完吗?
生:写不完。
师:这些小数真的和前面的数相等吗?结合数位顺序表我们一起来验证吧。
(学生在数位表中写出0.3,0.30,0.300,0.3000)
师:观察数位表,你发现了什么?
生:这些数十分位上都是三,其他数位上是0,所以大小是相等的。
师:0.3,0.30,0.300,0.3000它们的计数单位分别是多少?各自包含多少个计数单位?
生依次回答:0.3的计数单位是0.1,有3个0.1
0.30的计数单位是0.01,有30个0.01
0.300的计数单位是0.001,有300个0.001
0.3000的计数单位是0.0001,有3000个0.0001
师:从上往下观察这些数的计数单位和计数单位的个数,你发现了什么?
生:计数单位依次除以10,计数单位的个数依次乘10。
师:把计数单位除以10,计数单位乘10,结合起来看,它们的大小?
生齐答到:大小不变。
归纳性质:
师:通过不断的验证,我们发现小数具备怎样的性质?
生:小数添上0或去掉0,小数的大小不变。
师:嗯,这是你所发现的小数性质。其他同学都赞同他的说法吗?还有没有补充的?
生:我认为他说得不够完整,是在小数的末尾添上0或去掉0,小数的大小不变。要说明是小数的末尾。
师:哇!你的回答太精彩了,请把掌声送给严谨的小数学家。
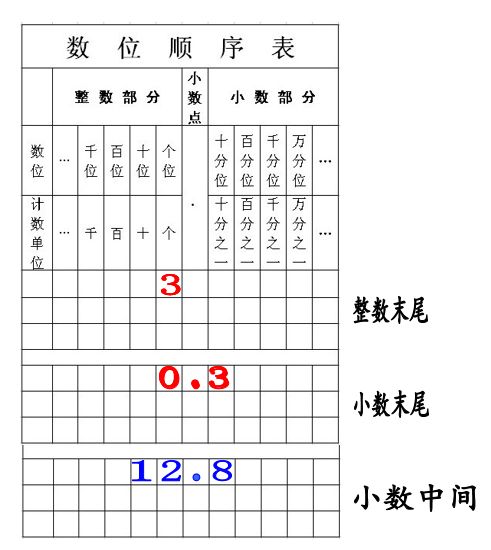
追问:刚刚我们说在小数的末尾添上0或去掉0,小数的大小不变。那么整数的末尾添上“0”或者去掉“0”,数的大小变不变呢?为什么?小数的中间添上或去掉“0”,数的大小变不变呢?为什么?(结合数位表探讨)
师:请在整数3的末尾添上一个0,两个0,并在数位表中写出这两个数。观察他们的大小有没有变化?
生:大小变了。
师:为什么整数末尾添0,大小就发生了变化?
生:因为3所在的数位发生了变化。
师:在小数12.8的中间添上0,观察它们的大小有没有发生变化?
生:1,2,8所在的数位变了,所以小数的大小也变了。
师:在小数0.3的末尾添上0,观察它们的大小有没有发生变化?
生:大小没变,因为它们的数位没变。
小结:只有在小数的末尾添上或去掉0,小数的大小不变。
设计意图:在学生初步感知的基础上,通过对比发现,能让学生更深刻地理解小数性质的意义。强化概念的严密性,为后面运用小数的性质打下坚实的基础
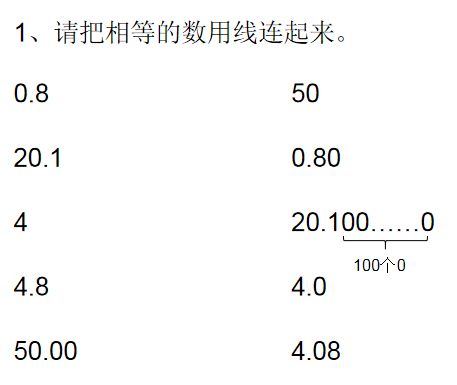
(学生独立完成并汇报)
注意:4.8与4.08这两个小数是不相等的。
三、联系生活,巩固性质
1、化简小数
老师在文具店中买了这两样文具,你觉得在付钱时怎样输入价钱更方便?
生:2.50直接输2.5,8.00直接输8
师:为什么可以这样输入?
生:根据小数的性质,小数末尾的0可以去掉,不会改变数的大小。
师:能将所学的数学知识巧妙地运用到生活中,真棒!根据小数的性质,像这样去掉小数末尾的0,这叫做“化简小数”。
(学生独立完成练习,并讲解化简方法)
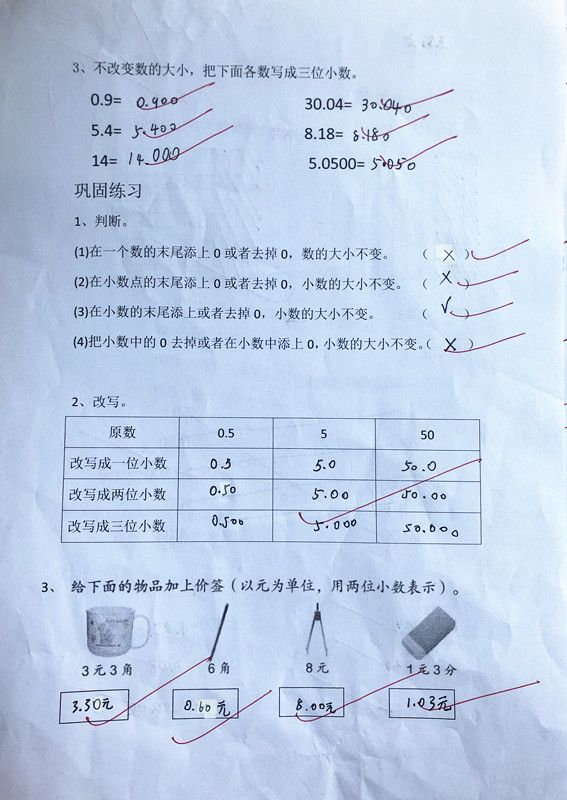
注意:0.080,80.020中,整数部分的0和十分位上的0都不能去掉,只能去掉末尾的0。
2、改写小数
师:也有其他的地方有类似的需要统一小数位数的要求。你能运用小数的性质,将下面的小数统一成三位小数吗?
课件出示:
(学生独立完成练习,并讲解改写方法)
生:0.2等于0.200
师:为什么在0.2末尾添上2个0就可以了?
生:因为0.2的小数部分有一位,还差两位,所以在它的末尾添上2个0就可以了。
生:4.08等于4.080
生:3等于3.000
师:为什么你在3的右下角点上小数点再添0?而不是在3的末尾直接添0?
生:直接添0,数位就会改变,那样就不相等了。
注意:整数改写成小数,必须先在个位右下角点上小数点,然后再在末尾添0。
设计意图:主要针对小数性质中的“小数”“末尾”等词进行巩固练习,强化概念。
结语
数学概念是抽象的,如何让学生对理性的思考感兴趣呢?那么就要创设合适的问题情境,以情入境,以情促思。只有使趣味性、生活化和应用性相结合,才能让学生真正感受数学学习是有血有肉、充满温情的。引导着学生从亲身经历猜测——探究——归纳总结的过程, 使学生在操作、讨论、验证中逐渐对“小数的性质”的本质有了深刻的理解。