【推荐系统】Graph Embedding系列之node2vec: Scalable Feature Learning for Networks

node2vec: Scalable Feature Learning for Networks

1. 论文地址：https://www.kdd.org/kdd2016/papers/files/rfp0218-groverA.pdf【KDD 2016】
2. Github实现：https://github.com/aditya-grover/node2vec（python/spark实现）
3. Github源码：https://github.com/snap-stanford/snap/tree/master/examples/node2vec （C++实现）
4. node2vec的软件实现(论文中给出的地址)：http://snap.stanford.edu/node2vec/

算法讲解：

1、论文前面的综述

Node2vec是对网络中的节点学习连续特征表达的算法框架，node2vec把节点映射到了一个“最大化保留节点的邻居节点的可能性”的低维空间。node2vec是针对可扩展网络特征学习的一个半监督算法，使用随机梯度下降(SGD)来优化一个传统的基于图的目标函数。直观地，node2vec生成了“在一个d维特征空间中使得保留了节点的邻居节点的可能性最大化”的特征表示。node2vec采用一个二阶随机游走方法来生成节点的网络邻居节点。

Node2vec的主要贡献在于灵活定义了一个节点的网络邻居。由于之前的算法没能够提供一个灵活的网络节点抽样方法，node2vec通过设计一个“与其他的抽样策略不相关的”灵活的目标函数并提供了调整网络空间的参数。

2、特征学习框架

网络中的特征学习可以看成是一个最大可能性的优化问题。

假设G=(V,E)是一个给定的（有向或者无向的、加权或者不加权的）网络，是我们想要学习用于预测实验的节点到特征表示的映射函数。这里，d是特征表示的维度参数，是一个|V|*d维度的参数矩阵。对于每个源节点，定义为节点通过邻居抽样策略S生成的网络邻居。

优化的目标函数为（下面的目标函数也可以当作是node2vec的目标函数）：

其中，是将顶点映射为embedding向量的映射函数。为了易于处理这个优化问题，这里提出两个标准假设：

• 条件独立性假设：给定源节点的特征表示的情况下，其一个邻居节点出现的概率独立于任何其他邻居节点：

• 特征空间内对称：源节点与其邻居节点在特征空间内有着彼此间的对称影响。通过将每个“源节点-邻居节点”对儿的条件概率作为被它们的特征之间的点积参数化的softmax单元（这里的理解貌似有点问题）：

有了这样的假设，公式(1)等价的目标函数就变成了（node2vec的目标函数）：

由于每个节点的配分函数（归一化因子）的计算代价问题，所以采用了负采样方法。这样，node2vec通过在模型参数上使用随机梯度下降方法来优化公式(2)。

由于网络不是线性的，以此不能像文本那样可以在连续词上使用滑动窗口来定义邻居的概念，node2vec提出了一个随机过程来抽样一个给定源节点的多个不同邻居节点。节点通过邻居抽样策略S生成的网络邻居节点不限制于直接邻居，而是根据不同的抽样策略S有着许多不同的结构。

3、BFS&DFS

可以把源节点的邻居节点抽样问题看成是一种局部检索的形式。为了能够公平地比较多个抽样策略S，我们限制了邻居集的规模为k个节点，并为单个节点抽样多个邻居节点集。通常，生成包含k个节点的邻居节点集有两种抽样策略：

• 宽度优先抽样(Breadth-first Sampling (BFS))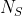：中的节点必须是源节点的直接邻居
• 深度优先抽样(Depth-first Sampling (DFS))：邻居节点由到源节点的距离逐渐增加的连续抽样组成

网络中节点的预测任务经常在两种相似性之间变换：同质性和结构等价，即内容相似性和结构相似性。

• 在同质性假设下，高度连通并且属于相似的网络聚类应该被embedded在一起（图1中的节点和节点属于相同的网络群体）。
• 然而在结构等价的假设下，在网络中有相似结构的节点应该被embedded在一起（图1中的节点和节点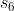是它们对应群体的中心节点）。

与同质性不同的是，结构性不强调连接，网络中离得很远的节点仍然有相同的网络角色。真实世界的网络可能是一些节点表现出同质性而另一些节点表现出结构性。

BFS和DFS在生成特征表示时要么反映同质性要么反映结构性。正因为这个特性，node2vec提出了一种将BFS和DFS结合的方法来选择邻居节点。

BFS抽样的邻居节点在embedding是更贴近结构性。通过对附近节点的搜索限制，BFS实现了对每个节点的邻居进行了一次微观扫描。此外，对BFS来说，被采样的邻居节点趋向于重复多次。这对于减少描述源节点的1-hop节点的分布变化来说，也是至关重要的（This is also important as it reduces the variance in characterizing the distribution of 1-hop nodes with respect the source node. ）。然而，对于给定的k，图中只有非常小的一部分被探索。

由于DFS可以从源节点走的更远，因此DFS能够探索网络中的更大部分。对DFS来说，抽样的节点更精确地反应出邻域的宏观扫描，宏观扫描可以根据同质性推断出网络群体。DFS不仅需要推断网络中点对点的相关性存在，同时需要描述出这些相关性的准确特征。当我们有一个抽样规模的限制和很大邻域去探索时，这很难做到。其次，过深度搜索由于一个被抽样节点可能远离源节点会导致复杂的相关性，也可能导致抽样缺乏代表性。

4、node2vec

node2vec的主要想法也是利用SkipGram的方法来为网络抽取特征表示，根据SkipGram的思路，最重要的就是定义这个Context，转移到网络中就是节点的邻居节点。那么如何抽样节点的邻居节点就成了研究的重点。node2vec采用了一种能够在BFS和DFS之间平滑过渡的邻域抽样策略：通过一种介于BFS和DFS之间的有偏随机游走来探索节点的邻域。

首先模拟一下固定长度为的一次随机游走，假设表示游走的第个节点，开始节点为。节点可以通过下面的公式生成：

也就是说，如果结点和节点之间有边，则以的概率选择下一个节点。这里，是节点和节点之间的非归一化转移概率，Z是标准化常数。

偏置随机游走的最简单的方法是根据静态的边权重进行下一个节点的抽样。然而，这种方法既不能解释网络结构又不能探索不同类型的网络邻居。此外，不像BFS或者DFS分别是适用于结构性和同质性的抽样范例，node2vec采用的随机游走策略表明这两个等价概念并不矛盾或者互斥，真实世界的网络通常可以采用二者的结合。

node2vec定义了一个带有两个参数和来引导游走的二阶随机游走，这也是node2vec算法的核心思想，这两个参数控制着【以多大的概率反复经过一些节点】和控制【“向内探索”还是“向外探索”】。这个二阶随机游走的目的可以简单理解为在DFS和BFS之间采取某种平衡。

假设当前随机游走顶点t经过边(t,v)到达顶点v，现在停留在顶点v，顶点v的下一个访问顶点x的概率可以根据公式  计算得到。

游走过程现在需要决定从t到v之后的下一步，于是对边(v,x)上的转移概率进行了评估。我们可以设置非归一化转移概率为：，这里：

是节点和节点之间的最短路径距离。由于中的只能取值0/1/2，因此，这两个参数和是完成游走的充要条件。

直觉上看，参数和控制着探索和离开节点和邻域节点的速度。尤其是和允许整个搜索过程近似在BFS和DFS之间，从而反应出节点等价性的不同概念间的一个密切关系。

结合图2理解一下参数p和参数q：

返回参数。参数控制着立即再次访问游走中节点的概率。将的值设置的较大（大于max(q,1)）可以保证以较低的可能性在接下来两步的游走中抽样到已经访问过的节点的（除非游走中的下一个节点没有其他邻居节点）。这个策略（将的值设置成大于max(q,1)）鼓励在抽样过程中的适度探索同时又避免了2-hop的冗余。如果的值较小（小于min(q,1)），将导致游走过程回溯一步，使得游走更接近开始节点。

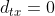• 只适用于的情况。
• p较大，以较低的可能性在接下来两步的游走中抽样到已经访问过的节点的（除非游走中的下一个节点没有其他邻居节点）。
• p较小，将导致游走过程回溯一步，使得游走更接近开始节点。

输入输出参数。参数运行搜索在inward节点和outward节点间进行区分。如果(q>1)，随机游走偏向于访问接近节点的节点。这样的游走得到底图的一个局部视图，这类似BFS抽样，抽样的节点由一小块区域的节点组成。如果(q<1)，游走更倾向于访问远离节点的节点。这类似DFS，倾向于向外探索。这里的一个本质区别是：node2vec在随机游走框架下实现了一个类似DFS的探索。因此，被抽样的节点在与给定节点的距离上不在严格递增，反过来，可以使得预处理的易处理并带来可观的随机游走抽样效率。通过将设置为随机游走中行进节点的一个函数，随机游走过程变成一个2阶马尔科夫过程。

• q>1，随机游走偏向于访问接近节点的节点，类似BFS，抽样的节点由一小块区域的节点组成。
• q<1，游走更倾向于访问远离节点的节点，类似DFS，倾向于向外探索。

简单总结一下参数和。

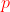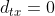• 参数控制重复访问刚刚访问过的顶点的概率。只适用于的情况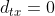，表示顶点x就是访问当前顶点v之前刚刚访问过的顶点。若的值较高，则访问刚刚访问过的节点的概率会降低；若的值较低，情况相反。将参数p设置为一个较大的值，可以确保我们以小概率采样到一个已经访问过的节点，除非下一个节点没有其他邻域节点了。
• 参数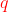控制的是对内游走还是对外游走。若(q>1)，游走倾向于访问和接近的节点，此时类似于BFS；若(q<1)，游走倾向于访问远离的节点，此时类似于DFS。

再谈谈纯粹的BFS/DFS随机游走方法有几个好处。就时间和空间而言，随机游走在计算层面很高效。存储图中每个节点的直接邻居节点的空间复杂度是O(|E|)。对于二阶随机游走而言，存储每个节点的邻居节点间的相互连接关系是很有用的，这消耗的空间复杂度是，这里是图中节点的平均度，真实网络中的这个值通常很小。随机游走优于传统的基于搜索的抽样策略的另一个关键优势在于时间复杂度。随机游走通过在不同源节点间复用抽样节点来提高有效抽样率（random walks provide a convenient mechanism to increase the effective sampling rate by reusing samples across different source nodes）。节点复用能够在整个过程中带来一些偏置，能够在很大程度上带来有效性。

通过模拟一个长度为的随机游走过程，根据随机游走的马尔科夫链特性，我们能够在一次为个节点抽样出个节点。这样，每个样本的有效的时间复杂度是。

Algorithm_1是node2vec算法的伪代码：

通过上面的伪代码可以看到，node2vec和deepwalk非常类似，主要区别在于顶点序列的采样策略不同。

由于开始结点的选择问题，每个在随机游走算法中都会存在一个隐式偏差，通过模拟次从每个节点开始的、固定长度为的随机游走来抵消掉这个偏差。在游走过程中的每一步，抽样根据转移概率完成。二阶马尔科夫链的转移概率可以预计算出来。这样，当模拟随机游走的时候节点的抽样可以使用alias sampling在O(1)的时间完成。

node2vec算法可以分为三个阶段，这三个阶段是连续执行的，其中的每个阶段可以并行且异步执行，这样能为node2vec带来更好的可扩展性。

• 预处理计算转移概率
• 随机游走模拟
• 使用随机梯度下降(SGD)优化

5、边特征学习

node2vec采用半监督的方法学习出网络中每个节点的特征表示。然而，实际中的预测任务经常会涉及到节点对而不是单个节点。例如，在链接预测中，我们会预计网络中的两个节点是否存在一条边。由于随机游走依赖于潜在网络中节点的连接结构，我们可以使用自展方法将其延伸到节点对而不是单个节点。给定两个节点和，我们在对应的特征向量和上定义一个二元运算，这样可以生成一个表示，，其中节点对(u,v)的表示维度。我们希望这个操作能够普遍定义到任何节点对上，即使这两个节点间不存在边，这样做可以使得学到的表示在链接预测任务中很有帮助。这样的二元操作也可以有多种选择。

参考代码：

• preprocess_transition_probs函数：

preprocess_transition_probs()函数的作用是生成两个采样预备数据：alias_nodes和alias_edges。两份数据又各自包含两个列表，这两个列表分别对应着alias采样中的概率和另一个选项。

alias_nodes：根据node和它的邻居之间的权重确定采样的概率，权重越高，被采中的概率越大。alias_nodes存储着在每个顶点时决定下一次访问其邻接点时需要的alias表（不考虑当前顶点之前访问的顶点）。

alias_edges：调用get_alias_edge()函数生成，返回在前一个访问顶点为t，当前顶点为v时决定下一次访问哪个邻接点时需要的alias表。

def preprocess_transition_probs(self):
	'''
	Preprocessing of transition probabilities for guiding the random walks.
	'''
	G = self.G
	is_directed = self.is_directed

	alias_nodes = {}  # 存储每个结点对应的两个采样列表
    # G.nodes()返回一个结点列表
	for node in G.nodes():
		unnormalized_probs = [G[node][nbr]['weight'] for nbr in sorted(G.neighbors(node))]  # 当前结点的邻居结点(有直连关系)的权重列表，如[1,1,1,1...]
		norm_const = sum(unnormalized_probs)  # 当前结点的邻居结点的权重求和
		normalized_probs =  [float(u_prob)/norm_const for u_prob in unnormalized_probs]  # 当前结点的邻居结点的权重占比,权重越大占比越大
		alias_nodes[node] = alias_setup(normalized_probs)  # 存储每个结点的邻居结点的权重占比

	alias_edges = {}
	triads = {}

	if is_directed:
        # G.edges()返回一个列表元组,列表里面是边关系,形如[(1,2), (1,3), ...]
        # (1,2)代表结点1和结点2之间有一条边
		for edge in G.edges():
			alias_edges[edge] = self.get_alias_edge(edge[0], edge[1])
	else:
		for edge in G.edges():
			alias_edges[edge] = self.get_alias_edge(edge[0], edge[1])
			alias_edges[(edge[1], edge[0])] = self.get_alias_edge(edge[1], edge[0])

	self.alias_nodes = alias_nodes
	self.alias_edges = alias_edges

	return

• node2vec_walk函数：

node2vec_walk函数是从start_node开始，生成walk_length长度的序列，序列的生成除了考虑当前节点，还考虑前一个遍历的节点。采样方法是根据之前生成的alias数据进行采样。由于采样时需要考虑前面2步访问过的顶点，所以当访问序列中只有1个顶点时，直接使用当前顶点和邻居顶点之间的边权作为采样依据。当序列多余2个顶点时，使用文章提到的有偏采样。

# walk_length: 随机游走序列长度
# start_node: 初始结点
# return: 列表，随机游走序列
def node2vec_walk(self, walk_length, start_node):
	'''
	Simulate a random walk starting from start node.
	'''
	G = self.G
	alias_nodes = self.alias_nodes
	alias_edges = self.alias_edges

	walk = [start_node]

	while len(walk) < walk_length:
		cur = walk[-1]
		cur_nbrs = sorted(G.neighbors(cur))  # 求当前结点的邻居结点
		if len(cur_nbrs) > 0:  # 如果存在邻居结点
			if len(walk) == 1:  # 如果序列中仅有一个结点,即第一次游走
				walk.append(cur_nbrs[alias_draw(alias_nodes[cur][0], alias_nodes[cur][1])])
			else:  # 如果序列中有多个结点
				prev = walk[-2]  # 找到当前游走结点的前一个结点
				next = cur_nbrs[alias_draw(alias_edges[(prev, cur)][0], 
					alias_edges[(prev, cur)][1])]
				walk.append(next)
		else:
			break

	return walk

•  simulate_walks函数：

simulate_walks函数对每个结点，根据num_walks得出其多条随机游走路径。

# 对每个结点,根据num_walks得出其多条随机游走路径
def simulate_walks(self, num_walks, walk_length):
	'''
	Repeatedly simulate random walks from each node.
	'''
	G = self.G
	walks = []
	nodes = list(G.nodes())
	print 'Walk iteration:'
	for walk_iter in range(num_walks):
		print str(walk_iter+1), '/', str(num_walks)
		random.shuffle(nodes)
		for node in nodes:
			walks.append(self.node2vec_walk(walk_length=walk_length, start_node=node))

	return walks

• get_alias_edge函数： 
• get_alias_edge()方法返回的是在上一次访问顶点t、当前访问顶点为v时，到下一个顶点x的未归一化转移概率。

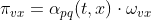# src: 随机游走序列种的上一个结点
# dst: 当前结点
def get_alias_edge(self, src, dst):
	'''
	Get the alias edge setup lists for a given edge.
	'''
	G = self.G
	p = self.p
	q = self.q

	unnormalized_probs = []
	for dst_nbr in sorted(G.neighbors(dst)):
		if dst_nbr == src:  # 返回源结点 d_tx=0
			unnormalized_probs.append(G[dst][dst_nbr]['weight']/p)
		elif G.has_edge(dst_nbr, src):  # 源结点和这个目标结点的邻居结点之间有直连边 d_tx=1
			unnormalized_probs.append(G[dst][dst_nbr]['weight'])
		else:  # 没有直连边 d_tx=2
			unnormalized_probs.append(G[dst][dst_nbr]['weight']/q)
	norm_const = sum(unnormalized_probs)
	normalized_probs =  [float(u_prob)/norm_const for u_prob in unnormalized_probs]  # 概率归一化

	return alias_setup(normalized_probs)  # 第一个返回值是Alias列表,第二个返回值是转移概率列表

 

实战技巧：

1、Spark实现

node2vec的spark实现：https://github.com/aditya-grover/node2vec，需要一个依赖：gensim，可以使用下面的命令安装：

pip install gensim

2、向量训练

向量训练可以使用Facebook开源的fastText工具，提前组织好训练数据的格式，扔里就行了。

3、遇到的坑1

直接从github拉下来的代码mvn打包之后，在spark上不能运行，会报出一个类似“Exception in thread "main" java.lang.NoSuchMethodError”的错误，应该是node2vec自带的pom文件的一些依赖版本的问题，可参考https://github.com/aditya-grover/node2vec/issues/61更新pom依赖。

 4、遇到的坑2

initTransitionProb()和randomWalk()这两个函数的逻辑貌似有点诡异...

参考博文：

• CSDN：笔记︱基于网络节点的node2vec、论文、算法python实现
• 知乎：关于Node2vec算法中Graph Embedding同质性和结构性的进一步探讨--王喆
• 知乎：【Graph Embedding】node2vec：算法原理，实现和应用--浅梦
• CSDN：node2vec论文阅读
• CSDN：论文阅读：node2vec: Scalable Feature Learning for Networks
• CSDN：时间复杂度O(1)的离散采样算法—— Alias method/别名采样方法
• 知乎：Alias Method:时间复杂度O(1)的离散采样方法