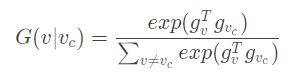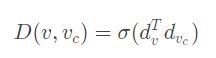从Random Walk（随机游走）到Graph Embedding（DeepWalk，LINE，Node2vec，SDNE，Graph2vec，GraphGAN）

前言

本文转载自csdn博主上杉翔二系列博客并外加一些自己收集的资料，在这里仅作为自己学习之用。

原文链接：https://blog.csdn.net/qq_39388410/article/details/87904974

1. 随机游走

普通数据挖掘方法大多都是确定性模型，对于输入的输出往往没有随机性，而一些能给出概率的随机性模型似乎更加的适用，如蒙特卡洛模拟，即模拟输入一堆的随机数进行评估。

1.1 几何布朗运动(Brownian motion)

布朗运动是将看起来连成一片的液体，在高倍显微镜下看其实是由许许多多分子组成的。液体分子不停地做无规则的运动，不断地随机撞击悬浮微粒。当悬浮的微粒足够小的时候，由于受到的来自各个方向的液体分子的撞击作用是不平衡的。在某一瞬间，微粒在另一个方向受到的撞击作用超强的时候，致使微粒又向其它方向运动，这样，就引起了微粒的无规则的运动就是布朗运动。（布朗运动指的是分子迸出的微粒的随机运动，而不是分子的随机运动。）

即布朗运动代表了一种随机涨落现象。普遍的观点仍认为，股票市场是随机波动的，随机波动是股票市场最根本的特性，是股票市场的常态。（随机现象的数学定义是：在个别试验中其结果呈现出不确定性；在大量重复试验中其结果又具有统计规律性的现象。）而布朗运动假设是现代资本市场理论的核心假设。

1.2 随机游走

随机游走（Random Walk，缩写为 RW），又称随机游动或随机漫步，是一种数学统计模型，它是一连串的轨迹所组成，其中每一次都是随机的。它能用来表示不规则的变动形式，如同一个人酒后乱步，所形成的随机过程记录。因此，它是记录随机活动的基本统计模型。其概念接近于布朗运动，是布朗运动的理想数学状态。

Random Walk 是随机过程（Stochastic Process）的一个重要组成部分，通常描述的是最简单的一维 Random Walk 过程。下面给出一个例子来说明：考虑在数轴原点处有一只蚂蚁，它从当前位置(记为 $x(t)$ )出发，在下一个时刻( $x(t+1)$)以 $\frac{1}{2}$ 的概率向前走一步(即 $x(t+1)=x(t)+1)$，或者以 $\frac{1}{2}$ 的概率向后走一步(即 $x(t+1)=x(t)-1$)，这样蚂蚁每个时刻到达的点序列 就构成一个一维随机游走过程。

一维、二维随机游走过程中，只要时间足够长，我们最终总能回到出发点;

三维网格中随机游走，最终能回到出发点的概率只有大约 34%；

四维网格中随机游走，最终能回到出发点的概率是 19.3% ；

八维空间中，最终能回到出发点的概率只有 7.3% ；

2. Graph Embedding

为什么要对图进行嵌入？

直接在这种非结构的，数量不定（可能数目非常多），属性复杂的 图 上进行机器学习/深度学习是很困难的，而如果能处理为向量将非常的方便。但评价一个好的嵌入需要：

• 保持图属性不变，如图的拓扑结构、顶点连接、顶点周围节点等
• 嵌入速度应该与图的大小无关
• 合适的维度以方便做下游任务

Graph Embedding
图嵌入本身其实是属于表示学习。主要目的是将图中的节点/图表示成低维，实值，稠密的向量形式，使得到的向量能够做进一步的推理，以更好的实现下游任务。图嵌入包括顶点嵌入/图嵌入，嵌入的方法主要有矩阵分解，随机游走和深度学习。

• 矩阵分解。因为从某种程度上图中的各节点关系可以视为稀疏的矩阵，那么基于矩阵分解的方法就可以得到低维的向量。其中常用的矩阵包括普通的邻接矩阵，度矩阵，拉普拉斯矩阵，节点转移概率矩阵，节点属性矩阵等。
• DeepWalk。通过对图随机游走得到一些序列，把序列当句子，利用word2vec就可以得到每一个“词”的向量了。（前提是基于句子某写词的出现和随机游走访问到的节点都服从幂律分布）。
• Graph Neural Network： Graph+Neural Network都是图神经网络GNN，通过结合深度学习来得到图嵌入也是很不错的选择。（矩阵分解也是可以结合神经网络的）

2.1 DeepWalk

出自2014的KDD，《DeepWalk: Online Learning of Social Representations》

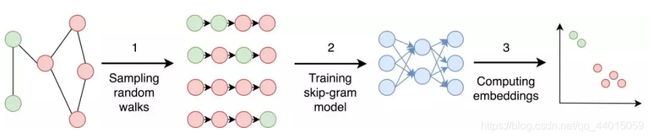
DeepWalk的思想如上图，具体就是从一个顶点出发，然后按照一定的概率随机移动到一个邻居节点，并将该节点作为新的当前节点，如此循环执行若干步，得到一条游走路径。然后把这个路径视为一个“句子”，用word2vec得到嵌入嵌入结果。

• 采样。通过随机游走对图进行采样。论文中作者建议从每个顶点执行32到64次随机游走就差不多了，具体游走代码如下。
• 将随机游走得到顶点路径当作word2vec中的句子。一般多使用skip-gram将随机游走顶点的one-hot向量作为输入，并最大化其相邻节点的预测概率。训练中通常预测20个邻居节点-左侧10个节点，右侧10个节点。
• 训练结束后的副产物，每个“词”的向量就是顶点的嵌入向量了。

def random_walk(self, path_length, alpha=0, rand=random.Random(), start=None):
    """ Returns a truncated random walk.
        path_length: Length of the random walk.
        alpha: probability of restarts.
        start: the start node of the random walk.
    """
    G = self #图G
    if start: #如果设置了开始节点
      path = [start]
    else:
      # 如果没有就随机选择
      path = [rand.choice(list(G.keys()))]

	#只要没到最大长度
    while len(path) < path_length:
      cur = path[-1]
      if len(G[cur]) > 0:
      	#按一定概率转移
        if rand.random() >= alpha:
          path.append(rand.choice(G[cur]))
        else:
          path.append(path[0])
      else:
        break
    return [str(node) for node in path]

可扩展：处理新加入节点，由于有random walk，所以只需要学习新的结点的信息就可以了
可并行：同时从不同的结点处开始random walk

2.2 LINE

出自2015WWW，《LINE: Large-scale Information Network Embedding》
github：https://github.com/tangjianpku/LINE

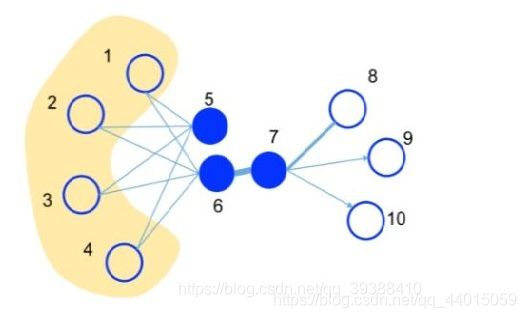
LINE也是一种基于邻域相似假设的方法（网络中相似的点在向量表示中的距离比较近），但DeepWalk可以视做是一个DFS，而LINE更加倾向于BFS。主要由一阶相似度和二阶相似度组成。First-order Proximity：一阶相似度用于描述图中成对顶点之间的局部相似度（两个顶点之间的相似），Second-order Proximity：二阶相似度是顶点的顶点之间的相似度，直观来说朋友的朋友也算是我们的朋友，这也同样应该是有效的，如上图的5和6之间虽然没有边，但是有4个相同的邻居节点，所以理论上我们认为5和6在二阶上是相似的。算法流程为：

• 模拟一阶相似度。顶点 $v_i$ 和 $v_j$ 之间的联合概率为
  
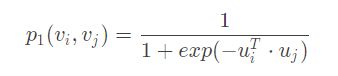
  $u$ 是节点对应的向量，向量越接近，点积就越大，联合概率也就越大。为了保持一阶相似性，将联合概率与经验概率(两点之间边的权值越大，经验概率越大)进行比较，即：
  
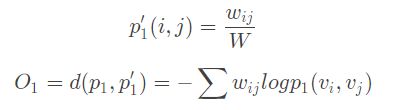
  $d$ 是衡量分布的函数，如果是 KL 散度来衡量则可以进一步展开，然后最小化该式子即可。另外，如果两节点之间无连接则直接设置为0。
• 模拟二阶相似度。也是定义一个 $v_j$ 是 $v_i$ 的邻居的概率为（二阶的度量是，如果 $v_j$ 和 $v_i$ 相似，那么对应向量点积越大，$v_j$ 越有可能是 $v_i$ 的邻居）
  
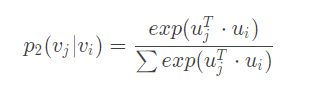
  同样与经验概率（此处定义为Graph中所有节点可能是 $v_i$ 邻居的概率）：
  
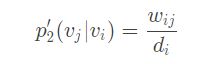
  其中 $w_{ij}$ 是边（$i$，$j$）的权重，$d_i$ 是顶点 $i$ 的出度。同时考虑到节点的重要程度可能不一样，所以加入度数作为权重，度数越高越重要。
  
• 分别训练一阶相似度模型和二阶相似度模型，然后拼接。

Trick：为了避免算二阶时需要遍历每个节点，LINE使用负采样的思想来简化计算。
Think：计算一阶相似度中改变同一条边的方向对于最终结果没有影响，所以一阶只适合无向图。而二阶有出度入度，能够实现有向图。
如何处理新加入的节点？ 根据经验分布和连接，优化O就可以了，其中原节点向量不变。

2.3 Node2vec

出自2016KDD，《node2vec: Scalable Feature Learning for Networks》

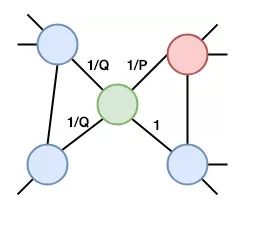
Node2vec 可以看作是对 DeepWalk 的一种更广义的抽象，主要是改进DeepWalk的随机游走策略。由于普通的随机游走无法很好地保留节点的局部信息，所以Node2vec多做了两个参数 $P$ 和 $Q$ 来加以控制（完全随机时P=Q=1），以获取邻域信息和更复杂的依存信息。

• In-out，参数 $Q$ 控制选择其他的新顶点的概率，偏广度优先，重视局部，即节点重要性。
• Return，参数 $P$ 控制返回原来顶点的概率，偏深度优先，重视全局，即群体重要性。

两个参数控制以达到BFS和DFS的平衡，具体如上图此时在绿色节点上，返回到前一步红色节点的概率是 $\frac{1}{P} $，到达未与先前红色节点连接的节点的概率为 $\frac{1}{Q}$，到达红色节点邻居的概率为1。

#不同之处只有转移的概率不同
def node2vec_walk(self, path_length, start):
    G = self 
    nodes = self.nodes
    edges = self.edges
    path = [start]
    while len(path) < path_length:        
        cur = path[-1]        
        cur_n = list(G.neighbors(cur)) #邻居节点       
        if len(cur_nbrs) > 0:            
            if len(path) == 1:                
                path.append(cur_n[sample(nodes[cur][0], nodes[cur][1])])            
            else:                
                prev = path[-2]                
                edge = (prev, cur)                
                next_node = cur_n[sample(edges[edge][0],edges[edge][1])]                
                path.append(next_node)        
        else:            
            break
    return walk

图嵌入的本质是什么？
实际上他们仍然还是矩阵分解！！具体如下图：

2.4 SDNE

github：https://github.com/suanrong/SDNE

前面整理了3种常用的图嵌入方法，DeepWalk，LINE和Node2vec。Structural Deep Network Embeddings（结构深层网络嵌入，SDNE）的不同之处在于，它并不是基于随机游走的思想，在实践中比较稳定。

主要思路如上图，会将节点向量 $s_i$ 作为模型的输入，通过自编码器对这个向量进行降维压缩 $z_i$，然后再重建特征。其损失函数定义为：

因为输入的是邻接矩阵，所以这样的重构能够使得结构相似的顶点具有相似的embedding表示向量。所以实际上通过重建学习到的是二阶相似度。

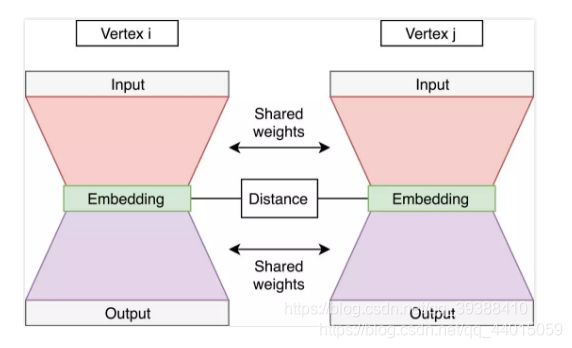
但是与LINE相似，SDNE也想保留一阶和二阶相似度，而且是想要同时优化，以同时捕获局部成对相似性和节点邻域结构的相似性。对于一阶相似度的计算，将架构变成如上图，由左右两个自编码器组成。一阶相似度的目标是计算节点间的相似性，那么可以利用起中间的嵌入得到的隐层向量z，然后计算左侧嵌入和右侧嵌z入间的距离。并可以用拉普拉斯矩阵优化一下计算：

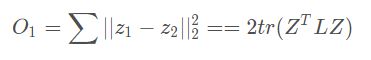
再加上正则项reg，总损失为：

def __make_loss(self, config):
        def get_1st_loss_link_sample(self, Y1, Y2):
            return tf.reduce_sum(tf.pow(Y1 - Y2, 2))
        def get_1st_loss(H, adj_mini_batch):
            D = tf.diag(tf.reduce_sum(adj_mini_batch,1))
            L = D - adj_mini_batch ## 拉普拉斯矩阵
            return 2*tf.trace(tf.matmul(tf.matmul(tf.transpose(H),L),H))

        def get_2nd_loss(X, newX, beta):
            B = X * (beta - 1) + 1
            return tf.reduce_sum(tf.pow((newX - X)* B, 2))
		#对w和b的正则化项
        def get_reg_loss(weight, biases):
            ret = tf.add_n([tf.nn.l2_loss(w) for w in weight.itervalues()])
            ret = ret + tf.add_n([tf.nn.l2_loss(b) for b in biases.itervalues()])
            return ret
            
        #总损失函数
        self.loss_2nd = get_2nd_loss(self.X, self.X_reconstruct, config.beta)
        self.loss_1st = get_1st_loss(self.H, self.adjacent_matriX)
        self.loss_xxx = tf.reduce_sum(tf.pow(self.X_reconstruct,2)) 
        self.loss_reg = get_reg_loss(self.W, self.b) 
        return config.gamma * self.loss_1st + config.alpha * self.loss_2nd + config.reg * self.loss_reg

其实似乎这个建模的思路和矩阵分解是差不多的，只是在降维时用的不是矩阵分解，而是自编码器，并融入了一阶与二阶的概念

2.5 Graph2vec

github:https://github.com/benedekrozemberczki/graph2vec

出自MLGWorkshop 2017的《graph2vec: Learning Distributed Representations of Graphs》
直接对整个图进行嵌入。一般比较容易想到的做法是Graph Pooling，著名的方法有Graph Coarsening，即用其他处理节点Embedding的方法处理后，然后逐渐合并聚类节点比如同一个class就归为一个超节点，最后变成一个向量。还有一类方法是node selection，即选部分的节点来代替。还有更直接的方法是直接max或者mean咯。

而Graph2Vec原理上和DeepWalk差不多，也是尝试借用word2vec来训练，只是这次为了嵌入整张图，所以尝试利用子图来训练。类似文档嵌入doc2vec，通过最大化作为输入的文档，来预测随机单词的可能性，Graph2vec预测图中子图的概率。

• 采样子图。为了提高效率，采样只选当前节点周围的邻接节点，构成子图sg。
  skip-gram。最大化输入图子图的概率 $J(\Phi )=-logP(s{g}_n^{(d)}|\Phi (G))$，$d$为度，$sg$为子图。

#把图处理成doc2vec问题的形式就可以用gensim了
from gensim.models.doc2vec import Doc2Vec, TaggedDocument

#得到Wisfeiler-Lehman特征
def do_a_recursion(self):
        new_features = {}
        for node in self.nodes:
            nebs = self.graph.neighbors(node)
            degs = [self.features[neb] for neb in nebs]
            features = [str(self.features[node])]+sorted([str(deg) for deg in degs])
            features = "_".join(features)
            hash_object = hashlib.md5(features.encode())
            hashing = hash_object.hexdigest()
            new_features[node] = hashing
        self.extracted_features = self.extracted_features + list(new_features.values())
        return new_features

2.6 Graph Generative Adversarial Nets（GraphGAN）

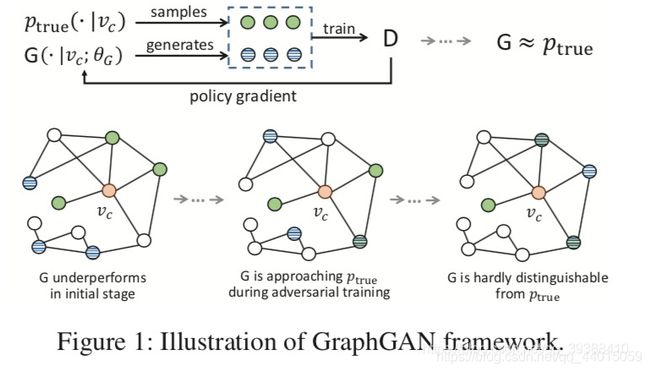
主要是将GAN的思想引入到图领域，简单来说也是和GAN一样，分为生成器和判别器：

• 生成器：在找网络中一个节点邻居的概率分布，也就是一个节点的连接偏好。
  
  即用softmax函数，输出邻居是每个节点的概率

• 判别器：以网络中的边为出发点，衡量两个节点之间是否有边关系。
  
  d分别代表两个节点的表示向量，如果v是采样的应该给高分，如果是生成的应该是低分。

值得注意的是在生成器的G中，如果要对每个节点都算一遍显然不划算，所以作者的解决方案是以某个节点为根节点BFS遍历形成一棵生成树（其实挺像随机游走的），然后计算树中两个节点之间的边对应的概率。

3. Graph Neural Network

图神经网络(Graph Neural Network, GNN)也是很好的图嵌入方法。GNN包括图卷积神经网络（GCN），图注意力网络（GAT），Graph LSTM等等，虽然技术上还是和CV，NLP领域内的方法很像。。。

图表征学习的局限

• 参数量大，每个顶点都有唯一的标准向量
• 不能给未出现的顶点生成表征向量
• 部分图表征学习不能融合属性特征等信息