第十一届蓝桥杯 2020年国赛真题 (Java 大学C组)

---

---

  在现场失误还是挺多的，

  就个人准备程度而言除了皮亚诺不敢分配时间去推导，其他的题都可以 $\mathrm{K}$ 掉，

  结果却是，应该只 $\mathrm{K}$ 了六七题，

  还好今年没特等，

  不然自己得给自己气死。

---

#A 美丽的 2

本题总分：5 分

---

问题描述

  小蓝特别喜欢 $2$，今年是公元 $2020$ 年，他特别高兴。
  他很好奇，在公元 $1$ 年到公元 $2020$ 年（包含）中，有多少个年份的数位中包含数字 $2$ ？

---

答案提交

  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

563

---

朴素解法

---

  签到

public class Test {

    public static void main(String[] args) { new Test().run(); }

    int N = 2020, ans = 0;

    void run() {
        for (int i = 1; i <= N; i++)
            if (i % 10 == 2|
                i / 10 % 10 == 2|
                i / 100 % 10 == 2|
                i / 1000 % 10 == 2) ans++;
        System.out.println(ans);
    }
}

---

分类讨论

---

  当数据规模较小且没有现成的程序时，

  可以简单的口算一下来节省编写程序的时间。

  我们可以将 $1\sim 2020$ 简单分为 $1\sim 999$ 、 $1001\sim 1999$ 和 $2000\sim 2020$ 三个区间 ，

  显然 $1000$ 不包含 $2$ 且 $1\sim 999$ 与 $1001\sim 1999$ 间包含 $2$ 的个数相等，

  再简单推导一下，

  $1\sim 9$ 有 $1+9\times 0=1$ 个数字包含 $2$，

  则 $1\sim 99$ 有 $10+9\times 1=19$ 个数字包含 $2$

  则 $1\sim 999$ 有 $100+9\times 19=271$ 个数字包含 $2$

  最后的结果就是 $2\times 271+21=563$，

  熟练后比写个程序快点，

  但也有玩脱的风险，

  过。

---

#B 合数个数

本题总分：5 分

---

问题描述

  一个数如果除了 $1$ 和自己还有其他约数，则称为一个合数。例如：$1$, $2$, $3$ 不是合数，$4$ ,$6$ 是合数。请问从 $1$ 到 $2020$ 一共有多少个合数。

---

答案提交

  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

1713

---

朴素解法

---

  双签到了

  朴素的去枚举复杂度在 $O(n\sqrt{n})$，

  这个数据下到无所谓，但当规模进一步扩大，就显得捉襟见肘了，

  所以下面会给出一个更为高效的解法。

public class Test {

    public static void main(String[] args) { new Test().run(); }

    int N = 2020, ans = 0;

    void run() {
        for (int i = 1; i <= N; i++)
            for (int k = 2; k * k <= i; k++)
                if (i % k == 0) {
                    ans++;
                    break;
                }
        System.out.println(ans);
    }
}

---

欧拉筛

---

  单独开了篇 博客，这里就不做展开了。

  一个大于 $1$ 的自然数，不是质数就是合数，因此将质数筛选出来，用原集合的大小减去所包含的质数个数就行了。

import java.util.ArrayList;
import java.util.List;

public class Test {

    public static void main(String[] args) { new Test().run(); }

    int N = 2020;

    void run() {
        boolean[] marked = new boolean[N + 1];
        List<Integer> primes = new ArrayList();
        for (int i = 2; i <= N; i++) {
            if (!marked[i])
                primes.add(i);
            for (int p : primes) {
                if (i * p > N) break;
                marked[i * p] = true;
                if (i % p == 0)break;
            }
        }
        System.out.println(N - primes.size() - 1);
    }
}

---

#C 扩散

本题总分：10 分

---

问题描述

  小蓝在一张无限大的特殊画布上作画。
  这张画布可以看成一个方格图，每个格子可以用一个二维的整数坐标表示。
  小蓝在画布上首先点了一下几个点：$(0,0)$，$(2020,11)$，$(11,14)$，$(2000,2000)$。只有这几个格子上有黑色，其它位置都是白色的。
  每过一分钟，黑色就会扩散一点。具体的，如果一个格子里面是黑色，它就会扩散到上、下、左、右四个相邻的格子中，使得这四个格子也变成黑色（如果原来就是黑色，则还是黑色）。
  请问，经过 $2020$ 分钟后，画布上有多少个格子是黑色的。

---

答案提交

  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

20312088

---

朴素解法

---

  简单做个广搜，

  需要注意的是坐标会扩散到负数，

  所以需要设定一个偏移量。

import java.util.ArrayDeque;
import java.util.Queue;

public class Test {

    public static void main(String[] args) { new Test().run(); }

    int N = 2020, ans = 0, offset = N;

    void run() {
        boolean[][] visited = new boolean[N * 3 + 1][N * 3 + 1];
        Queue<Point> queue = new ArrayDeque();
        queue.offer(new Point(0, 0, 0));
        queue.offer(new Point(0, 2020, 11));
        queue.offer(new Point(0, 11, 14));
        queue.offer(new Point(0, 2000, 2000));
        while (queue.peek().time <= N) {
            Point p = queue.poll();
            if (!visited[p.x + offset][p.y + offset]) {
                queue.add(new Point(p.time + 1, p.x + 1, p.y));
                queue.add(new Point(p.time + 1, p.x, p.y + 1));
                queue.add(new Point(p.time + 1, p.x - 1, p.y));
                queue.add(new Point(p.time + 1, p.x, p.y - 1));
                visited[p.x + offset][p.y + offset] = true;
                ans++;
            }
        }
        System.out.println(ans);
    }

    class Point {

        short time, x, y;

        Point(int time, int x, int y) {
            this.time = (short)time;
            this.x = (short)x;
            this.y = (short)y;
        }
    }
}

  除此之外还有

  广度最广可达 $4\times 4\times \mathrm{N}\times \mathrm{k}$，$\mathrm{k}$ 大概是一个 $2\sim 4$ 之间的实数。

  群里面有个好兄弟广搜爆堆了，

  所以这里要注意一下内存的控制，

  前车之鉴。

---

朴素改进

---

  一个点扩散多次，“广度”呈线性增长，

  这似乎并不是不能接受，

  但上解给出的代码已经需要明显的等待时间才能计算出结果，

  这促使我们去寻找一个更好的策略，

  比如给定一个点集，判断有多少个点是给定点中某个可达的。

public class Test {

    public static void main(String[] args) { new Test().run(); }

    int N = 2020, ans = 0;

    int[][] sources = { {0, 0}, {2020, 11}, {11, 14}, {2000, 2000} };

    void run() {
        for (int x = -N; x <= N << 1; x++)
            for (int y = -N; y < N << 1; y++)
                for (int[] source : sources)
                    if (Math.abs(x - source[0]) + Math.abs(y - source[1]) <= N) {
                        ans++; break;
                    }
        System.out.println(ans);
    }
}

  一个点扩散到未被扩散的点需要的时间与到该点的曼哈顿距离意义相同，

  能力有限，这里便不做展开。

---

#D 阶乘约数

本题总分：10 分

---

问题描述

  定义阶乘 $n!=1\times 2\times 3\times \cdot \cdot \cdot \times n$。
  请问 $100!$ （$100$ 的阶乘）有多少个约数。

---

答案提交

  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

39001250856960000

---

乘法原理

---

  每届必考的算术基本定理。

public class Test {

    public static void main(String[] args) { new Test().run(); }

    int N = 100;
    long ans = 1;

    void run() {
        int[] factors = new int[N];
        for (int i = 1, n, p; i <=  N; i++) {
            for (n = i, p = 2; p * p <= n; p++)
                while (n % p == 0) {
                    factors[p]++;
                    n /= p;
                }
            if (n > 1) factors[n]++;
        }
        for (int factor : factors)
            if (factor != 0) ans *= factor + 1;
        System.out.println(ans);
    }
}

  求质因子的指数，相乘就完了，

  相关的网上有很多，也过了。

---

#E 本质上升序列

本题总分：15 分

---

问题描述

  小蓝特别喜欢单调递增的事物。
  在一个字符串中，如果取出若干个字符，将这些字符按照在字符串中的顺序排列后是单调递增的，则成为这个字符串中的一个单调递增子序列。
  例如，在字符串 $\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{q}\mathrm{i}\mathrm{a}\mathrm{o}$ 中，如果取出字符 $\mathrm{n}$ 和 $\mathrm{q}$，则 $\mathrm{n}\mathrm{q}$ 组成一个单调递增子序列。类似的单调递增子序列还有 $\mathrm{l}\mathrm{n}\mathrm{q}$、$\mathrm{i}$、$\mathrm{a}\mathrm{n}\mathrm{o}$ 等等。
  小蓝发现，有些子序列虽然位置不同，但是字符序列是一样的，例如取第二个字符和最后一个字符可以取到 $\mathrm{a}\mathrm{o}$，取最后两个字符也可以取到 $\mathrm{a}\mathrm{o}$。
  小蓝认为他们并没有本质不同。
  对于一个字符串，小蓝想知道，本质不同的递增子序列有多少个？
  例如，对于字符串 $\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{q}\mathrm{i}\mathrm{a}\mathrm{o}$，本质不同的递增子序列有 $21$ 个。它们分别是 $\mathrm{l}$、$\mathrm{a}$、$\mathrm{n}$、$\mathrm{q}$、$\mathrm{i}$、$\mathrm{o}$、$\mathrm{l}\mathrm{n}$、$\mathrm{a}\mathrm{n}$、$\mathrm{l}\mathrm{q}$、$\mathrm{a}\mathrm{q}$、$\mathrm{n}\mathrm{q}$、$\mathrm{a}\mathrm{i}$、$\mathrm{l}\mathrm{o}$、$\mathrm{a}\mathrm{o}$、$\mathrm{n}\mathrm{o}$、$\mathrm{i}\mathrm{o}$、$\mathrm{l}\mathrm{n}\mathrm{q}$、$\mathrm{a}\mathrm{n}\mathrm{q}$、$\mathrm{l}\mathrm{n}\mathrm{o}$、$\mathrm{a}\mathrm{n}\mathrm{o}$、$\mathrm{a}\mathrm{i}\mathrm{o}$。
  请问对于以下字符串（共 $200$ 个小写英文字母，分四行显示）：（如果你把以下文字复制到文本文件中，请务必检查复制的内容是否与文档中的一致。在试题目录下有一个文件 inc.txt，内容与下面的文本相同）

tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhf
iadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqij
gihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmad
vrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl

  本质不同的递增子序列有多少个？

---

答案提交

  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

3616159

---

朴素解法

---

  我有一个 $O(2^n)$ 的算法，

  可惜这里大小合适，

  我能写下。

import java.io.*;
import java.util.HashSet;
import java.util.Set;

public class Test {

    public static void main(String[] args) { new Test().run(); }

    Set<String> set = new HashSet();

    String str = "";

    void run() {
        try (BufferedReader in = new BufferedReader(new InputStreamReader(new FileInputStream("inc.txt")))) {
            for (String line = in.readLine(); line != null; line = in.readLine()) str += line;
            dfs(new  StringBuilder(), '\0', 0);
            System.out.println(set.size() - 1);
        } catch (Exception e) {
            e.printStackTrace();
        }
    }

    void dfs(StringBuilder builder, char last, int depth) {
        if (depth == str.length()) set.add(builder.toString());
        else {
            dfs(builder, last, depth + 1);
            if (str.charAt(depth) > last) {
                builder.append(str.charAt(depth));
                dfs(builder, str.charAt(depth), depth + 1);
                builder.deleteCharAt(builder.length() - 1);
            }
        }
    }
}

---

状压枝剪

---

  写出上面这么个东西其实很冒进的，

  但 $\mathrm{C}\mathrm{P}\mathrm{U}$ 在 $3.5\mathrm{G}\mathrm{h}\mathrm{z}$ 下大约五分钟就出了结果。

  这一定程度上是可遇见的，

  一是蓝桥很少出面面俱到的数据，

  二是序列全由小写字母组成，

  也就是说，最多有 $2^{26}$ 种可能的本质上升序列，

  枝剪 $+$ 状压 应该能在四小时内乱搞过任意$(n\le 200)$数据。

import java.io.*;

public class Test {

    public static void main(String[] args) { new Test().run(); }

    boolean[] set = new boolean[1 << 26];

    int[] map = new int[0x7F];

    int ans = -1, N;

    String str = "";

    void run() {
        try (BufferedReader in = new BufferedReader(new InputStreamReader(new FileInputStream("inc.txt")))) {
            for (String line = in.readLine(); line != null; line = in.readLine()) str += line;
            for (char c = 'a'; c <= 'z'; c++) map[c] = 1 << c - 'a';
            N = str.length();
            dfs(0, 0, 0);
            System.out.println(ans);
        } catch (Exception e) {
            e.printStackTrace();
        }
    }

    void dfs(int buff, int last, int depth) {
        if (set[buff]) return;
        if (depth == N) {
            set[buff] = true;
            ans++;
        } else {
            if (map[str.charAt(depth)] > last)
                dfs(buff | map[str.charAt(depth)], map[str.charAt(depth)], depth + 1);
            dfs(buff, last, depth + 1);
        }
    }
}

  虽然是道简单题，

  但已经能体现出出题人想反乱搞是一件多么困难的事情，

  还有就是，注意搜索的顺序。

---

动态规划

---

  其实题目给出了就已经明牌 $\mathrm{D}\mathrm{P}$ 了。

  设原串为 $S(0,N]$，$f_{i,c}$ 为 $S(0,i]$ 中以 $c$ 结尾的本质不同上升序列的个数，

  显然$$f_{i,c}=\{\begin{array}{lr}{f}_{i-1,c}& S[i]\ne c\\ 1+{\sum }_{c^{\prime }\mid c^{\prime }<S[i]}{f}_{i-1,c^{\prime }}& S[i]=c\end{array}$$  没什么营养的 $\mathrm{D}\mathrm{P}$。

import java.io.*;

public class Test {

    public static void main(String[] args) { new Test().run(); }

    String str = "";

    void run() {
        try (BufferedReader in = new BufferedReader(new InputStreamReader(new FileInputStream("inc.txt")))) {
            for (String line = in.readLine(); line != null; line = in.readLine()) str += line;
            int N = str.length(), ans = 0;
            int[][] dp = new int[N + 1][0x7F];
            for (int i = 1; i <= N; i++) {
                for (char c = 'a'; c <= 'z'; c++)
                    dp[i][c] = dp[i - 1][c];
                char now = str.charAt(i - 1);
                dp[i][now] = 1;
                for (char c = 'a'; c < now; c++)
                    dp[i][now] += dp[i - 1][c];
            }
            for (char c = 'a'; c <= 'z'; c++)
                ans += dp[N][c];
            System.out.println(ans);
        } catch (Exception e) {
            e.printStackTrace();
        }
    }
}

---

#F 天干地支

时间限制: 1.0s 内存限制: 512.0MB 本题总分：15 分

---

问题描述

  古代中国使用天干地支来记录当前的年份。
  天干一共有十个，分别为：甲（$\text{jiaˇ}$）、乙（$\text{yıˇ}$）、丙（$\text{bıˇng}$）、丁（$\text{dıˉng}$）、戊（$\text{wuˋ}$）、己（$\text{jıˇ}$）、庚（$\text{geˉng}$）、辛（$\text{xıˉn}$）、壬（$\text{reˊn}$）、癸（$\text{guıˇ}$）。
  地支一共有十二个，分别为：子（$\text{zıˇ}$）、丑（$\text{choˇu}$）、寅（$\text{yıˊn}$）、卯（$\text{maˇo}$）、辰（$\text{cheˊn}$）、巳（$\text{sıˋ}$）、午（$\text{wuˇ}$）、未（$\text{weˋi}$）、申（$\text{sheˉn}$）、酉（$\text{yoˇu}$）、戌（$\text{xuˉ}$）、亥（$\text{haˋi}$）。

  将天干和地支连起来，就组成了一个天干地支的年份，例如：甲子。
  $2020$ 年是庚子年。
  每过一年，天干和地支都会移动到下一个。例如 $2021$ 年是辛丑年。
  每过 $60$ 年，天干会循环 $6$ 轮，地支会循环 $5$ 轮，所以天干地支纪年每 $60$ 年轮回一次。例如 $1900$ 年，$1960$ 年，$2020$ 年都是庚子年。
  给定一个公元纪年的年份，请输出这一年的天干地支年份。

---

输入格式

  输入一行包含一个正整数，表示公元年份。

---

输出格式

  输出一个拼音，表示天干地支的年份，天干和地支都用小写拼音表示（不表示声调），之间不要加入任何多余的字符。

---

测试样例₁

Input：
2020

Output：
gengzi

---

评测用例规模与约定

  对于所有评测用例,输入的公元年份为不超过 $9999$ 的正整数。

---

  签到题，

  别看了。

import java.util.Scanner;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    public void run() {
        String[] stems = { "jia", "yi", "bing", "ding", "wu", "ji", "geng", "xin", "ren", "gui" },
                 branches = { "zi", "chou", "yin", "mao", "chen", "si", "wu", "wei", "shen", "you", "xu", "hai" };
        int n = new Scanner(System.in).nextInt();
        System.out.print(stems[(n + 6)% 10] + branches[(n + 8) % 12]);
    }
}

  以 $2020$ 为基准算一下偏移量就行。

---

#G 皮亚诺曲线距离

时间限制: 1.0s 内存限制: 512.0MB 本题总分：20 分

---

问题描述

  皮亚诺曲线是一条平面内的曲线。
  下图给出了皮亚诺曲线的 $1$ 阶情形，它是从左下角出发，经过一个 $3\times 3$ 的方格中的每一个格子，最终到达右上角的一条曲线。

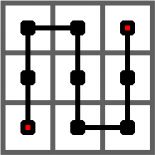
  下图给出了皮亚诺曲线的 $2$ 阶情形，它是经过一个 $3^2\times 3^2$ 的方格中的每一个格子的一条曲线。它是将 $1$ 阶曲线的每个方格由 $1$ 阶曲线替换而成。

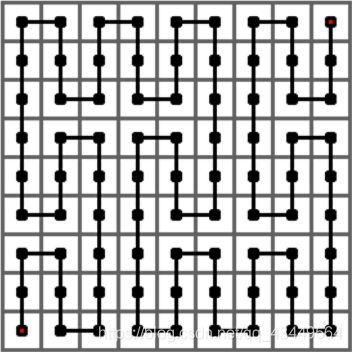
  下图给出了皮亚诺曲线的 $3$ 阶情形，它是经过一个 $3^3\times 3^3$ 的方格中的每一个格子的一条曲线。它是将 $2$ 阶曲线的每个方格由 $1$ 阶曲线替换而成。

  皮亚诺曲线总是从左下角开始出发，最终到达右上角。
  我们将这些格子放到坐标系中，对于 k 阶皮亚诺曲线，左下角的坐标是
($0$, $0$)，右上角坐标是 ($3^k-1$, $3^k-1$)，右下角坐标是 ($3^k-1$, $0$)，左上角坐标是($0$, $3^k-1$)。
  给定 k 阶皮亚诺曲线上的两个点的坐标，请问这两个点之间，如果沿着皮亚诺曲线走，距离是到少？

---

输入格式

  输入的第一行包含一个正整数 $k$，皮亚诺曲线的阶数。
  第二行包含两个整数 $x_1$, $y_1$，表示第一个点的坐标。
  第三行包含两个整数 $x_2$, $y_2$，表示第二个点的坐标。

---

输出格式

  输出一个整数，表示给定的两个点之间的距离。

---

测试样例₁

Input：
1
0 0
2 2

Output：
8

测试样例₂

Input：
2
0 2
0 3

Output：
13

---

评测用例规模与约定

  对于 $30$% 的评测用例，$0\le k\le 10$。
  对于 $50$% 的评测用例，$0\le k\le 20$。
  对于所有评测用例，$0\le k\le 100,0\le x_1,y_1,x_2,y_2<3^k,x_1,y_1,x_2,y_2\le 10^{18}$。
  数据保证答案不超过 $10^{18}$。

---

分形问题

---

  如 $\mathrm{P}\mathrm{e}\mathrm{a}\mathrm{n}\mathrm{o}\mathrm{C}\mathrm{u}\mathrm{r}\mathrm{v}\mathrm{e}$ 这种，以一定规律无限包含自身的图，可以被称为分形图。

  其衍生出的问题，自然是分形问题。

  我们设 $calc(x,y)=(0,0)$ 到 $(x,y)$ 的距离，

  显然答案等于 $abs(calc(x_1,y_1)-calc(x_2,y_2))$。

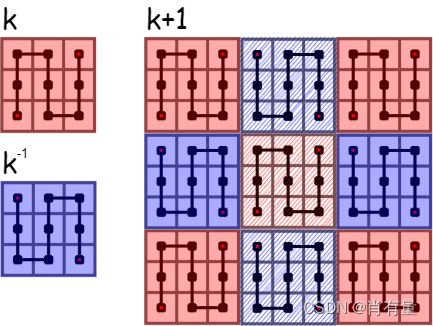
  不难看出，一个 $k+1$ 阶皮亚诺曲线由 $2$ 种 $k$ 阶皮亚诺曲线连接构成，$k>0$。

  相信大伙看到这个图就已经知道程序怎么实现了，过。

  其中一种 $k$ 阶皮亚诺曲线为另一种的水平翻转，即 $y$ 轴坐标取反，而中线这段皮亚诺曲线与其他曲线的区别在于起点与终点相反，我可以计算出其中一种，再用曲线的大小减去它。

  综上我们可以选择一个策略，

  先按离原点的距离将 $k$ 阶皮亚诺曲线分成 $0\sim 8$ 块 $k-1$ 阶曲线，显然在这个意义上 $k-1$ 阶曲线与 $k-1$ 阶曲线的水平翻转交替出现，如果坐标落在 $k-1$ 阶曲线的水平翻转上，$y$ 取其模 $3^{k-1}$ 的补数。

  再递归计算坐标所在的 $k-1$ 曲线离其原点的距离，如果坐标落在中线上则用 $k-1$ 阶曲线的长度减去递归计算到的距离，最后加上编号乘以 $k-1$ 阶曲线的长度，

  就得到了一个点到原点的距离。

import java.util.Scanner;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    long[] pow;

    void run() {
        Scanner in = new Scanner(System.in);
        int k = in.nextInt(), i;
        long x1 = in.nextLong();
        long y1 = in.nextLong();
        long x2 = in.nextLong();
        long y2 = in.nextLong();
        pow = new long[k + 2];
        for (i = 2, pow[1] = 1; i <= k; i++)
            pow[i] = pow[i - 1] * 3;
        System.out.println(Math.abs(calc(k, x1, y1) - calc(k, x2, y2)));
    }

    long calc(int k, long x, long y) {
        if (k == 0) return 0;
        long offset = x /  pow[k] * 3;
        boolean flag = offset == 3;
        offset += flag ? (3 - y /  pow[k] - 1) : (y /  pow[k]);
        if ((offset & 1) == 1)
            x =  pow[k] - x %  pow[k] - 1;
        return flag ? ((offset + 1) * pow[k] * pow[k] - calc(k - 1, x %  pow[k], y %  pow[k]) - 1) :
                (offset *  pow[k] * pow[k] + calc(k - 1, x %  pow[k], y %  pow[k])) ;
    }
}

  不过显然这个程序是不能通过全部数据的。

  因为 $k$ 最大为 $100$，也就是皮亚诺曲线最长为 $3^{200}$，

  只使用基本数据类型的话，

  装不下，怎么想都装不下吧。

  因此我们需要在此基础上继续完善。

---

两种完善

---

  一种朴素的思路是，

  不多逼逼，

  BigInteger 走起。

import java.math.BigInteger;
import java.util.Scanner;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    BigInteger[] pow;

    void run() {
        Scanner in = new Scanner(System.in);
        int k = in.nextInt(), i;
        pow = new BigInteger[k + 2];
        for (i = 2, pow[1] = BigInteger.valueOf(1); i <= k; i++)
            pow[i] = pow[i - 1].multiply(BigInteger.valueOf(3));
        System.out.println(
        	calc(k, in.nextBigInteger(), in.nextBigInteger()).
            subtract(
            calc(k, in.nextBigInteger(), in.nextBigInteger())).
            abs());
    }

    BigInteger calc(int k, BigInteger x, BigInteger y) {
        if (k == 0) return BigInteger.valueOf(0);
        long offset = x.divide(pow[k]).multiply(BigInteger.valueOf(3)).longValue();
        boolean flag = offset == 3;
        offset += (flag ? (BigInteger.valueOf(2).subtract(y.divide(pow[k]))) : y.divide(pow[k])).longValue();
        if ((offset & 1) == 1)
            x = pow[k].subtract(x.mod(pow[k])).subtract(BigInteger.valueOf(1));
        return flag ? BigInteger.valueOf(offset + 1).multiply(pow[k]).multiply(pow[k]).subtract(calc(k - 1, x.mod(pow[k]), y.mod(pow[k]))).subtract(BigInteger.valueOf(1)) : 
        			  BigInteger.valueOf(offset).multiply(pow[k]).multiply(pow[k]).add(calc(k - 1, x.mod(pow[k]), y.mod(pow[k])));
    }
}

  当然这份程序能否全部测试用例，

  也还是存疑的，

  毕竟曲线的长度呈指数增长，

  复合到高精度整形的乘法上，常数较大且复杂度最低也为 $O(n^3\log n)$。

  当然 100 还是不算大，并且蓝桥叫你用个 BigInteger 已经顶了天了。

  因此我们需要结合一些其他的信息，将数的操作范围控制在长整形可操作范围之内。

  比如数据保证答案不超过 $10^{18}$。

  在一个 $k$ 阶皮亚诺曲线中，相距最远的两个点为起点和终点，也就是说，

  若数据给定的两点分别在 $k$ 阶曲线中起点和终点所在的 $k-1$ 阶曲线中，那么这个 $k$ 不会大于 $19$，因为 $k^{2\times 19}\approx 1.3E18$，

  而若数据给定两点在 $k$ 阶曲线中相邻的两个 $k-1$ 阶曲线中，则 $k$ 不会大于 $20$，因为当两点需要通过三个 $k-1$ 阶曲线连通时，$k-1$ 阶曲线的长度不会大于 $10^{18}$。

  先求三进制公共最长前缀将问题缩放至一个 $k$ 阶皮亚诺曲线，使得曲线包含数据给定两点且 $k$ 最小。

  虽然 $9\times k^{2\times 19}$ 显然超过了 $2^{63}-1$ 即一个长整形可表示的正整数的范围，但我们可以在此基础上继续采取一些策略，

  比如手写int128，或者根据两点所在的块之间的位置关系做特判等等。

  这里我要采取的策略是重新定义答案的表示形式，

  不想打字了，直接看代码吧。

import java.util.Scanner;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    long N = 450283905890997363L, ans = 0;

    int[][] idx = {{0, 1, 2}, {5, 4, 3}, {6, 7, 8}};

    void run() {
        Scanner in = new Scanner(System.in);
        in.next();
        long x1 = in.nextLong();
        long y1 = in.nextLong();
        long x2 = in.nextLong();
        long y2 = in.nextLong();
        boolean sign1 = true, sign2 = true, turn1, turn2;
        int offset1, offset2;
        for (int i = 38; i > 0; i--) {
            offset1 = idx[(int)(x1 / N)][(int)(y1 / N)];
            offset2 = idx[(int)(x2 / N)][(int)(y2 / N)];
            turn1 = (offset1 & 1) == 1;
            turn2 = (offset2 & 1) == 1;
            if (x1 / N == 1) {
                offset1++;
                if (sign1) ans--; else ans++;
            }
            if (x2 / N == 1) {
                offset2++;
                if (sign2) ans++; else ans--;
            }
            ans += ((sign1 ? offset1 : -offset1) - (sign2 ? offset2 : -offset2)) * N * N;
            if (x1 / N == 1) sign1 = !sign1;
            if (x2 / N == 1) sign2 = !sign2;
            if (turn1) x1 = N - x1 % N - 1;
            else x1 %= N;
            if (turn2) x2 = N - x2 % N - 1;
            else x2 %= N;
            y1 %= N;
            y2 %= N;
            N /= 3;
        }
        System.out.println(ans > 0 ? ans : -ans);
    }
}

  主要是 $\mathrm{J}\mathrm{a}\mathrm{v}\mathrm{a}$ 不能指针乱飞，

  写的不是很舒服，

  摆烂了。

---

#H 蓝肽子序列

时间限制: 1.0s 内存限制: 512.0MB 本题总分：20 分

---

问题描述

  $L$ 星球上的生物由蛋蓝质组成，每一种蛋蓝质由一类称为蓝肽的物资首尾连接成一条长链后折叠而成。
  生物学家小乔正在研究 $L$ 星球上的蛋蓝质。她拿到两个蛋蓝质的蓝肽序列，想通过这两条蓝肽序列的共同特点来分析两种蛋蓝质的相似性。
  具体的，一个蓝肽可以使用 $1$ 至 $5$ 个英文字母表示，其中第一个字母大写，后面的字母小写。一个蛋蓝质的蓝肽序列可以用蓝肽的表示顺序拼接而成。
  在一条蓝肽序列中，如果选取其中的一些位置，把这些位置的蓝肽取出，并按照它们在原序列中的位置摆放，则称为这条蓝肽的一个子序列。蓝肽的子序列不一定在原序列中是连续的，中间可能间隔着一些未被取出的蓝肽。
  如果第一条蓝肽序列可以取出一个子序列与第二条蓝肽序列中取出的某个子序列相等，则称为一个公共蓝肽子序列。
  给定两条蓝肽序列，找出他们最长的那个公共蓝肽子序列的长度。

---

输入格式

  输入两行，每行包含一个字符串，表示一个蓝肽序列。字符串中间没有空格等分隔字符。

---

输出格式

  输出一个整数，表示最长的那个公共蓝肽子序列的长度。

---

测试样例₁

Input：
LanQiaoBei
LanTaiXiaoQiao

Output：
2

Explanation：
最长的公共蓝肽子序列为 LanQiao，共两个蓝肽。

---

评测用例规模与约定

  对于 $20$% 的评测用例，两个字符串的长度均不超过 $20$。
  对于 $50$% 的评测用例，两个字符串的长度均不超过 $100$。
  对于所有评测用例，两个字符串的长度均不超过 $1000$。

---

  $\mathrm{L}\mathrm{C}\mathrm{S}$，签到，送分。

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    void run() {
        try (BufferedReader in = new BufferedReader(new InputStreamReader(System.in))) {
            String A = in.readLine();
            String B = in.readLine();
            int[] AUpper = new int[0x3FF];
            int[] BUpper = new int[0x3FF];
            int N = 0, M = 0;
            for (int i = 0; i < A.length(); i++)
                if (Character.isUpperCase(A.charAt(i))) AUpper[++N] = i;
            for (int i = 0; i < B.length(); i++)
                if (Character.isUpperCase(B.charAt(i))) BUpper[++M] = i;
            int[][] dp = new int[N + 1][M + 1];
            AUpper[N + 1] = A.length();
            BUpper[M + 1] = B.length();
            boolean flag;
            for (int i = 1; i <= N; i++)
                for (int j = 1; j <= M; j++) {
                    if (flag = AUpper[i + 1] - AUpper[i] == BUpper[j + 1] - BUpper[j]) {
                        for (int i1 = AUpper[i], i2 = BUpper[j]; i1 < AUpper[i + 1]; i1++, i2++)
                            if (A.charAt(i1) != B.charAt(i2)) {
                                flag = false;
                                break;
                            }
                        if (flag) dp[i][j] = dp[i - 1][j - 1] + 1;
                    }
                    if (!flag) dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                }
            System.out.println(dp[N][M]);
        } catch (IOException e) {
            e.printStackTrace();
        }
    }

    int max(int a, int b) { return a > b ? a : b; }
}

---

#I 画廊

时间限制: 1.0s 内存限制: 512.0MB 本题总分：25 分

---

问题描述

  小蓝办了一个画展，在一个画廊左右两边陈列了他自己的作品。为了使画展更有意思，小蓝没有等距陈列自己的作品，而是按照更有艺术感的方式陈列。
  在画廊的左边陈列了 $L$ 幅作品，在画廊的右边陈列了 $R$ 幅作品，左边的作品距离画廊的起点依次为 u₁, u₂, · · · , u_L，右边的作品距离画廊起点依次为 v₁, v₂, · · · , v_R。
  每周，小蓝要整理一遍自己的每一幅作品。整理一幅作品的时间是固定的，但是要带着沉重的工具。从一幅作品到另一幅作品之间的距离为直线段的长度。
  小蓝从画廊的起点的正中央（左右两边的中点）出发，整理好每一幅画，最终到达画廊的终点的正中央。已知画廊的宽为 $w$。
  请问小蓝最少带着工具走多长的距离？

---

输入格式

  输入的第一行包含四个整数 $L,R,d,w$，表示画廊左边和右边的作品数量，以及画廊的长度和宽度。
  第二行包含 $L$ 个正整数 u₁, u₂, · · · , u_L，表示画廊左边的作品的位置。
  第三行包含 $R$ 个正整数 v₁, v₂, · · · , v_R，表示画廊右边的作品的位置。

---

输出格式

  输出一个实数，四舍五入保留两位小数，表示小蓝最少带着工具走的距离。

---

测试样例₁

Input：
3 3 10 2
1 3 8
2 4 6

Output：
14.71

Explanation：
小蓝从起点开始，首先到达左边第一幅作品（走动距离 √2），然后到达左
边第二幅作品（走动距离 2），然后到达右边第一幅作品（走动距离 √5），然后
到达右边第二幅和第三幅作品（走动距离 2 和 2），然后到达左边第三幅作品（走动距离 2√2），最后到达画廊终点（走动距离 √5）。
总共距离为 √2 + 2 + √5 + 2 + 2 + 2 √2 + √5 ≈ 14.71。

---

评测用例规模与约定

  对于 $40$% 的评测用例，$1\le L,R\le 10,1\le d\le 100,1\le w\le 100$。
  对于 $70$% 的评测用例，$1\le L,R\le 100,1\le d\le 1000,1\le w\le 1000$。
  对于所有评测用例，$1\le L,R\le 500,1\le d\le 100000,1\le w\le 100000,0\le$ u₁ $<$ u₂ $<\cdot \cdot \cdot <$ u_L $\le d,0\le$ v₁ $<$ v₂ $<\cdot \cdot \cdot <$ v_R $\le d$。

---

动态规划

---

  $\mathrm{T}\mathrm{S}\mathrm{P}$，$\mathrm{N}\mathrm{P}$ 完全问题，

  从这个意义上来看，

  只能 $\mathrm{D}\mathrm{P}$ 求解了，

  毕竟蓝桥嘛，dddd。

import java.io.IOException;
import java.io.InputStream;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

import static java.lang.Math.hypot;
import static java.lang.Math.min;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    void run() {
        InputReader in = new InputReader(System.in);
        int L = in.readInt(), R = in.readInt(), d = in.readInt();
        double w = in.readInt();
        int[] left = new int[L + 1];
        int[] right = new int[R + 1];
        for (int i = 1; i <= L; i++)
            left[i] = in.readInt();
        for (int i = 1; i <= R; i++)
            right[i] = in.readInt();
        double[][][] dp = new double[2][L + 1][R + 1];
        for (int i = 1; i <= L; i++) {
            dp[1][i][0] = Double.POSITIVE_INFINITY;
            dp[0][i][0] = hypot(w / 2, left[1]) + left[i] - left[1];
        }
        for (int i = 1; i <= R; i++) {
            dp[0][0][i] = Double.POSITIVE_INFINITY;
            dp[1][0][i] = hypot(w / 2, right[1]) + right[i] - right[1];
        }
        for (int i = 1; i <= L; i++)
            for (int j = 1; j <= R; j++) {
                dp[0][i][j] = min(dp[0][i - 1][j] + left[i] - left[i - 1], dp[1][i - 1][j] + hypot(w, right[j] - left[i]));
                dp[1][i][j] = min(dp[0][i][j - 1] + hypot(w, left[i] - right[j]), dp[1][i][j - 1] + right[j] - right[j - 1]);
            }
        System.out.printf("%.2f", min(dp[0][L][R] + hypot(w / 2, d - left[L]), dp[1][L][R] + hypot(w / 2, d - right[R])));
    }

    class InputReader {

        BufferedReader reader;
        StringTokenizer token;

        InputReader(InputStream in) {
            this.reader = new BufferedReader(new InputStreamReader(in));
        }

        String read() {
            while (token == null || !token.hasMoreTokens()) {
                try {
                    token = new StringTokenizer(reader.readLine());
                } catch (IOException e) {
                    e.printStackTrace();
                }
            }
            return token.nextToken();
        }

        int readInt() { return Integer.parseInt(read()); }
    }
}

---

#J 答疑

时间限制: 3.0s 内存限制: 512.0MB 本题总分：25 分

---

问题描述

  有 $n$ 位同学同时找老师答疑。每位同学都预先估计了自己答疑的时间。
  老师可以安排答疑的顺序，同学们要依次进入老师办公室答疑。
  一位同学答疑的过程如下：
  1. 首先进入办公室，编号为 $i$ 的同学需要 $s_i$ 毫秒的时间。
  2. 然后同学问问题老师解答，编号为 $i$ 的同学需要 $a_i$ 毫秒的时间。
  3. 答疑完成后，同学很高兴，会在课程群里面发一条消息，需要的时间可以忽略。
  4. 最后同学收拾东西离开办公室，需要 $e_i$ 毫秒的时间。一般需要 $10$ 秒、$20$ 秒或 $30$ 秒，即 $e_i$ 取值为 $10000$，$20000$ 或 $30000$。

  一位同学离开办公室后，紧接着下一位同学就可以进入办公室了。
  答疑从 $0$ 时刻开始。老师想合理的安排答疑的顺序，使得同学们在课程群里面发消息的时刻之和最小。

---

输入格式

  输入第一行包含一个整数 $n$，表示同学的数量。
  接下来 $n$ 行，描述每位同学的时间。其中第 $i$ 行包含三个整数 $s_i$, $a_i$, $e_i$，意义如上所述。

---

输出格式

  输出一个整数，表示同学们在课程群里面发消息的时刻之和最小是多少。

---

测试样例₁

Input：
3
10000 10000 10000
20000 50000 20000
30000 20000 30000

Output：
280000

Explanation：
按照 1, 3, 2 的顺序答疑，发消息的时间分别是 20000, 80000, 180000。

---

评测用例规模与约定

  对于 $30$% 的评测用例，$1\le n\le 20$。
  对于 $60$% 的评测用例，$1\le n\le 200$。
  对于所有评测用例，$1\le n\le 1000$，$1\le s_i\le 60000$，$1\le a_i\le 1000000$，$e_i\in \{10000,20000,30000\}$，即 $e_i$ 一定是 $10000、20000、30000$ 之一。

---

  题目大意就是，求出一个 $n$ 级排列 $S$，

  使得 $\sum _{I=0}^n(\sum _{i=0}^{I-1}(s_{S_i}+a_{S_i}+e_{S_i})+s_{S_I}+a_{S_I})$ 最小，

  简单将公式变形后

  $\sum _{I=1}^n\sum _{i=1}^I(s_{S_i}+a_{S_i}+e_{S_i})-\sum _{i=1}^n{e}_i$

  我们会发现任意情况下，结果都与 $e$ 相对无关，而在前项中 $\forall i\in [1,n]$ 对结果的贡献为 $在当前排列倒序所处位置\times (s_i+a_i+e_i)$，

  显然，$s_i+a_i+e_i$ 越大的学生的答疑放在越后面，结果最小。

  签到题。

import java.io.IOException;
import java.io.InputStream;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
import java.util.Arrays;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    void run() {
        InputReader in = new InputReader(System.in);
        int n = in.readInt();
        long offset = 0, ans = 0;
        Mate[] mates = new Mate[n];
        for (int i = 0; i < n; i++)
            mates[i] = new Mate(in.readInt(), in.readInt(), in.readInt());
        Arrays.sort(mates);
        for (int i = 0; i < n; i++) {
            ans += offset + mates[i].offset;
            offset += mates[i].block;
        }
        System.out.println(ans);
    }

    class Mate implements Comparable<Mate> {

        int offset, block;

        Mate(int s, int a, int e) { block = e + (offset = s + a); }

        public int compareTo(Mate mate) { return this.block - mate.block; }
    }

    class InputReader {

        BufferedReader reader;
        StringTokenizer token;

        InputReader(InputStream in) {
            this.reader = new BufferedReader(new InputStreamReader(in));
        }

        String read() {
            while (token == null || !token.hasMoreTokens()) {
                try {
                    token = new StringTokenizer(reader.readLine());
                } catch (IOException e) {
                    e.printStackTrace();
                }
            }
            return token.nextToken();
        }

        int readInt() { return Integer.parseInt(read()); }
    }
}

  还用 TreeMap 写另一个版本。

import java.io.IOException;
import java.io.InputStream;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
import java.util.TreeMap;
import java.util.Map;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    void run() {
        InputReader in = new InputReader(System.in);
        int n = in.readInt(), e, m, t, sae;
        long ans = 0;
        TreeMap<Integer, Integer> tree = new TreeMap();
        for (int i = 0; i < n; i++) {
            sae = in.readInt() + in.readInt();
            sae += e = in.readInt();
            tree.put(sae, tree.getOrDefault(sae, 0) + 1);
            ans -= e;
        }
        for (Map.Entry<Integer, Integer> entry : tree.entrySet()) {
            t = entry.getKey();
            m = entry.getValue();
            ans += ((n -= m) * m + m * (m + 1L) / 2) * t;
        }
        System.out.println(ans);
    }

    class InputReader {

        BufferedReader reader;
        StringTokenizer token;

        InputReader(InputStream in) {
            this.reader = new BufferedReader(new InputStreamReader(in));
        }

        String read() {
            while (token == null || !token.hasMoreTokens()) {
                try {
                    token = new StringTokenizer(reader.readLine());
                } catch (IOException e) {
                    e.printStackTrace();
                }
            }
            return token.nextToken();
        }

        int readInt() { return Integer.parseInt(read()); }
    }
}