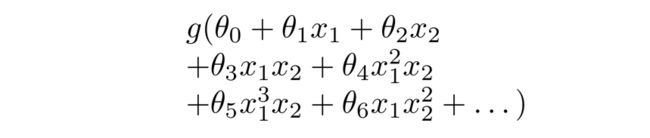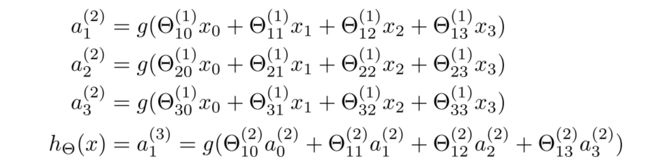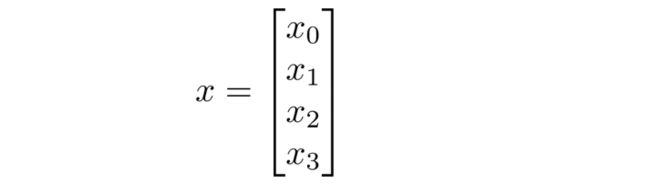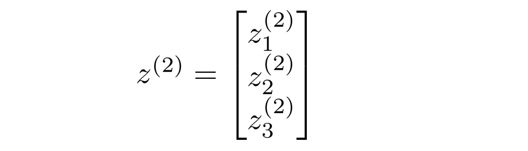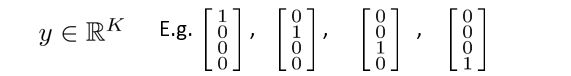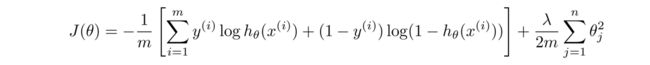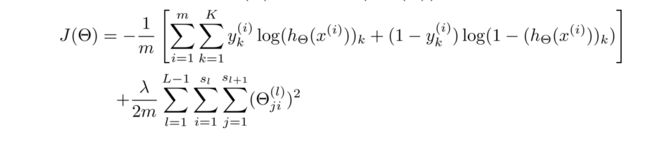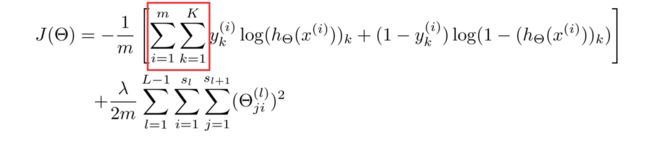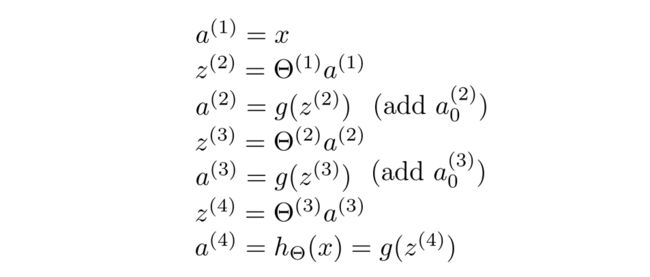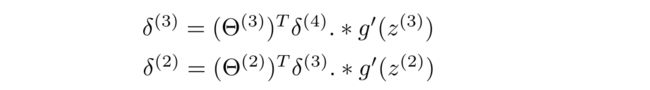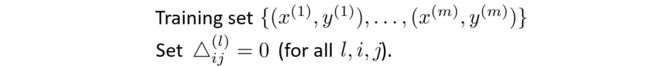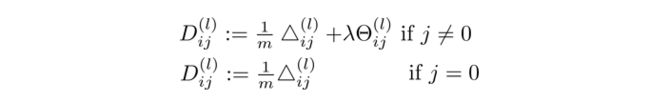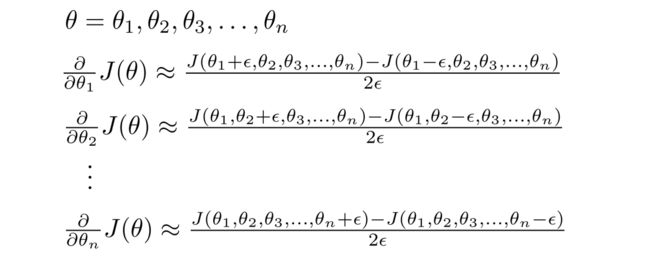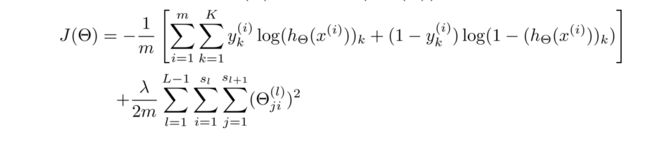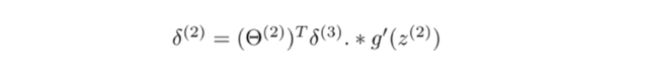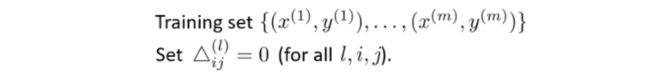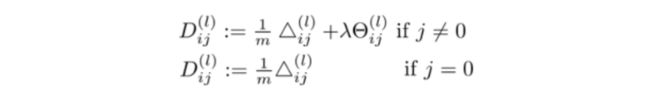【机器学习】神经网络识别手写数字(附python源码)
专栏持续更新中,欢迎订阅~
Linux
数据结构与算法
机器学习
文章目录
-
- 非线性假设
- 神经元与大脑
- 正向传播:向量化实现
- 神经网络中的特征值
- 代价函数
- 反向传播算法
- 梯度检测
- 训练神经网络过程总结
- 吴恩达机器学习练习4
- 源文件领取
非线性假设
我们先来说一下在有线性回归和Logistic回归的基础上,为什么还要用神经网络。
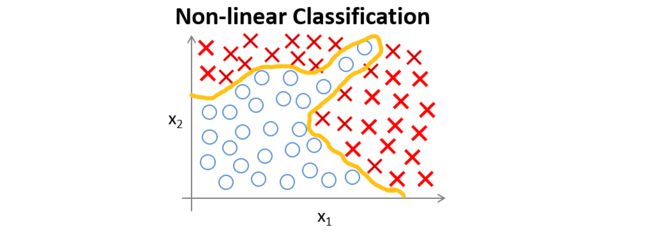
假如有一个如下图所示的监督学习分类问题。
如果运用Logistic回归来解决,则需要构造一个如下图所示包含很多非线性项的Logistic回归函数,当项数足够多时,就能够将样本进行分类。
但我们也发现了,这个分类问题仅仅包含两个特征值而已,我们暂且还能将两个特征值的所有交互项包含到多项式中。
但很多时候我们面临的分类问题所包含的特征值远不止两项,如果还用Logistic回归,那么要添加的项是非常多的。
下面我们来看看神经网络是如何解决这一问题的。
神经元与大脑
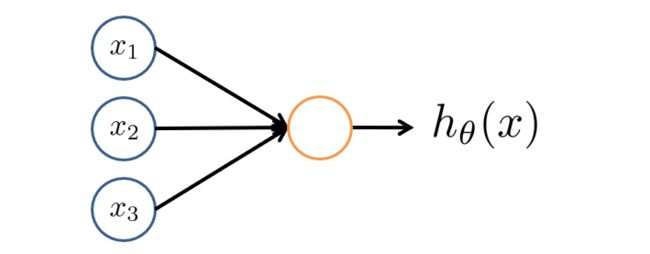
现在我们用如下模型来将神经元模拟成一个逻辑单元,左边箭头为输入,右边箭头为输出。
有时我们会称该逻辑单元为带有sigmoid或者logistic激活函数的人工神经元。
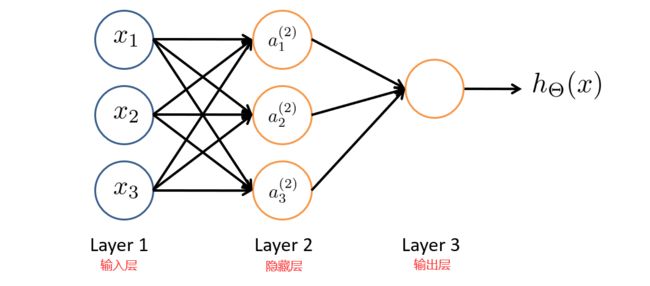
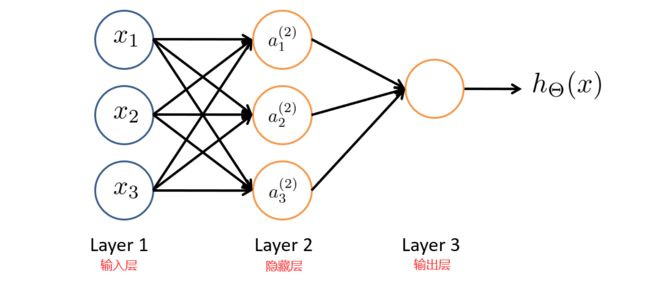
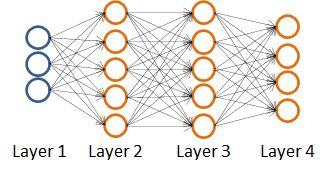
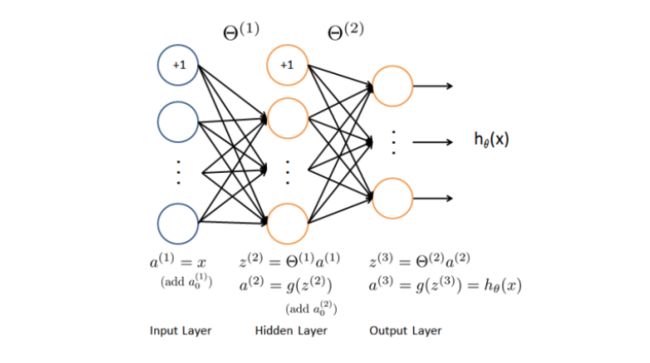
神经网络就是由多个神经元连接在一起的集合,如下图所示。
神经网络的第一层称为输入层,输入特征值。
第二层称为隐藏层,实际上任何非输入层和非输出层都被称为隐藏层,后面我们会提到。
第三层称为输出层,输出假设结果。
为了解释这个神经网络具体的计算步骤我们再解释一下上图中的一些记号。
a i ( j ) a^{(j)}_i ai(j):表示第 j j j层的第 i i i个激活项。
θ ( j ) \theta^{(j)} θ(j):表示权重矩阵,控制第 j j j层到第 j + 1 j+1 j+1层的映射。
那么,隐藏层三个激活值可表示成如下sigmoid函数值:
这样我们就更直观地看出了权重矩阵 θ ( 1 ) \theta^{(1)} θ(1)控制着第一层到第二层的映射,并且 θ ( 1 ) \theta^{(1)} θ(1)是一个 3 × 4 3×4 3×4的矩阵。
权重矩阵 θ ( 2 ) \theta^{(2)} θ(2)控制着第二层到第三层的映射,并且 θ ( 2 ) \theta^{(2)} θ(2)是一个 1 × 4 1 ×4 1×4的矩阵。
如果一个神经网络的第 j j j层有 s j s_j sj个单元,第 j + 1 j+1 j+1层有 s j + 1 s_{j+1} sj+1个单元,则权重矩阵 θ ( j ) \theta^{(j)} θ(j)是一个 s j + 1 × ( s j + 1 ) s_{j+1}×(s_j+1) sj+1×(sj+1)的矩阵。
经过上面的分析,我们得出了以下步骤:先通过前三个方程计算出三个隐藏单元的激活值,然后利用这些激活值计算 h θ ( x ) h_{\theta}(x) hθ(x),最后输出。
正向传播:向量化实现
为了实现向量化,接下来我们定义一些额外的项。
我们做如下替换
现在我们发现了上面的的数字块似乎对应了矩阵向量乘法,接下来我们就能进行
神经网络的向量化了。
下面我们将 x x x定义为:
将 z ( 2 ) z^{(2)} z(2)定义为:
于是有
z ( 2 ) = θ ( 1 ) x z^{(2)}=\theta^{(1)}x z(2)=θ(1)x
求出了 z ( 2 ) z^{(2)} z(2), a ( 2 ) a^{(2)} a(2)也就可以求出来了
a ( 2 ) = g ( z ( 2 ) ) a^{(2)}=g(z^{(2)}) a(2)=g(z(2))
至此,第一层到第二层的映射解决了,现在来看第二层到第三层的映射:
我们需要在前面求得的 a ( 2 ) a^{(2)} a(2)中添加一个偏置项 a 0 ( 2 ) = 1 a^{(2)}_0=1 a0(2)=1
那么 z ( 3 ) = θ ( 2 ) a ( 2 ) z^{(3)}=\theta^{(2)}a^{(2)} z(3)=θ(2)a(2)
最终 h θ ( x ) = a ( 3 ) = g ( z ( 3 ) ) h_{\theta}(x)=a^{(3)}=g(z^{(3)}) hθ(x)=a(3)=g(z(3))
好了,来到这里估计大家都晕了,再来回顾一下整个求算过程吧。
从输入单元的激活项开始,向前传播给隐藏层,计算出隐藏层的激活项,然后继续向前传播,再计算输出层的激活项,这个从输入层到隐藏层再到输出层的过程就叫向前传播。
神经网络中的特征值
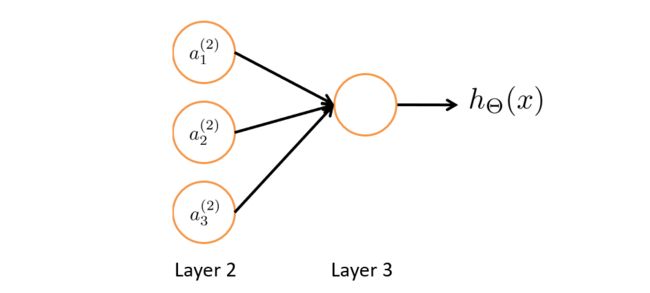
如下图我们先把输入层暂时去掉,其实思路就和Logistic回归一样了,就是通过第二层的特征值,然后利用第三层的逻辑回归单元来预测 h θ ( x ) h_{\theta}(x) hθ(x)的值。
神经网络和Logistic回归不同的是,Logistic回归的特征值 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3是数据集直接给出的,但神经网络的特征值并不是原来的特征值 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3,还要向前传播计算得到新的 a 1 ( 2 ) 、 a 2 ( 2 ) 、 a 3 ( 2 ) a^{(2)}_1、a^{(2)}_2、a^{(2)}_3 a1(2)、a2(2)、a3(2)作为新的特征值。
代价函数
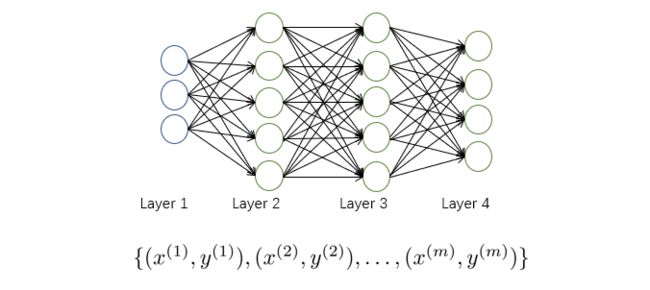
假设我们有如下训练集:
我们用 L L L表示神经网络的层数, s l s_l sl表示第 l l l层中神经元的个数(不包含偏置项)。
这里的输出单元有四个,输出的 h θ ( x ) h_{\theta}(x) hθ(x)是一个四维向量,即输出的预测值 y y y为以下几个情况:
在神经网络中,我们使用的代价函数 是逻辑回归中使用的代价函数的一般形式:
但由于 y y y是一个k(k=4)维向量,因此代价函数改造为:
这里稍微解释一下这个代价函数,首先看第一项的求和,这里输出有四个单元,故k=4,其实就是在逻辑函数的输出的基础上,依次把4个代价函数加起来。
再看看正规项的求和,这里有三个求和号,由于权重矩阵 θ ( j ) \theta^{(j)} θ(j)是一个 s j + 1 × ( s j + 1 ) s_{j+1}×(s_j+1) sj+1×(sj+1)的矩阵,但由于不包含偏差项,少了一列,所以变成 s j + 1 × s j s_{j+1}×s_j sj+1×sj,故正规项是对每一层的权重矩阵求和,再加起来。
反向传播算法
在得到神经网络的代价函数后,按照惯例下一步我们我们要做的就是最小化函数,而导数项的计算则需要用到反向传播算法。
首先我们来回顾一下正向传播:
计算步骤如下:
下面来介绍一下这个反向传播:
首先我们用 δ j ( l ) \delta^{(l)}_j δj(l)表示第 l l l层第 j j j个单元的激活值的误差。
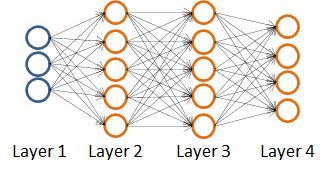
我们以上图四层(L=4)的神经网络为例
如第四层第 j j j个激活项的误差为:
δ j ( 4 ) = a j ( 4 ) − y j \delta^{(4)}_j=a^{(4)}_j-y_j δj(4)=aj(4)−yj
这个误差就是假设输出值与真实值之间的差。
同样我们可以进行向量化变成:
δ ( 4 ) = a ( 4 ) − y \delta^{(4)}=a^{(4)}-y δ(4)=a(4)−y
求出 δ ( 4 ) \delta^{(4)} δ(4)后,我们再进行反向传播求出 δ ( 3 ) \delta^{(3)} δ(3)、 δ ( 2 ) \delta^{(2)} δ(2),输入层不需要考虑误差项,故不需要计算 δ ( 1 ) \delta^{(1)} δ(1),以下过程不作证明:
其中
g ′ ( z ( 3 ) ) = a ( 3 ) . ∗ ( 1 − a ( 3 ) ) g^{'}(z^{(3)})=a^{(3)}.*(1-a^{(3)}) g′(z(3))=a(3).∗(1−a(3))
g ′ ( z ( 2 ) ) = a ( 2 ) . ∗ ( 1 − a ( 2 ) ) g^{'}(z^{(2)})=a^{(2)}.*(1-a^{(2)}) g′(z(2))=a(2).∗(1−a(2))
最后总结起来,对于一个训练集,我们首先令所有的偏导为0,注意这里的△就是代表 δ \delta δ.
跳出循环后,我们再计算以下式子:
这里的 D i j ( l ) D^{(l)}_{ij} Dij(l)就是代价函数关于每个参数的偏导了。
梯度检测
刚刚我们说了如何用向前传播和反向传播来计算导数,但反向传播算法实现起来很困难,而且很容易出现bug,和梯度下降结合到一起后,它运行得还不错,并且在每次迭代之后,代价函数也在不断缩小,但如果存在一些bug,那最终得出的神经网络会有一个较大的误差。
那么如何去验证我们使用的反向传播是正确的呢,现在提出了一种梯度检测的思想,几乎可以解决所有这种问题,下面我们就在看看什么是梯度检测。
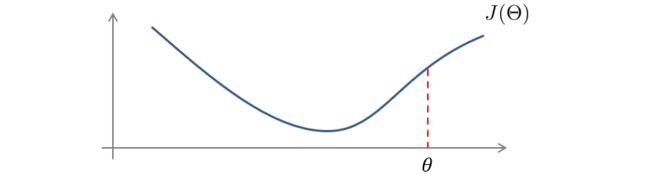
如果要计算 θ \theta θ对应点的正切,我们可以利用数值上的近似来求。
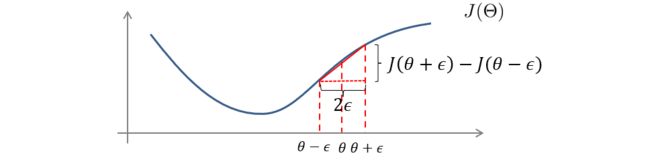
首先我们取一个很小的值 ϵ \epsilon ϵ,然后计算出 θ + ϵ \theta+\epsilon θ+ϵ和 θ − ϵ \theta-\epsilon θ−ϵ对应点的数值,这两点连线的斜率就近似等于 θ \theta θ的正切。
d d θ J ( θ ) ≈ J ( θ + ϵ ) − J ( θ − ϵ ) 2 ϵ \frac{d}{d\theta}J(\theta)≈\frac{J(\theta+\epsilon)-J(\theta-\epsilon)}{2\epsilon} dθdJ(θ)≈2ϵJ(θ+ϵ)−J(θ−ϵ)
刚刚我们只考虑了 θ \theta θ为实数的时候,接下来我们再推广到 θ \theta θ为向量参数的情况,则计算过程如下所示。
(假设 θ \theta θ是一个n维向量)
总结:
- 通过反向传播来求出 D i j ( l ) D^{(l)}_{ij} Dij(l).
- 通过梯度检测求出偏导(gradApprox)。
- 验证 D i j ( l ) D^{(l)}_{ij} Dij(l)是否近似等于 g r a d A p p r o x gradApprox gradApprox。
- 完成前面的步骤,也就是验证了我们的反向传播算法是正确的。在进行神经网络的学习时,注意要去掉梯度检测,因为这是一个计算量大,计算时间长的过程。
训练神经网络过程总结
选择合适的神经网络架构
- 确定输入单元的数量,也就是输入特征值的维度 x ( i ) x^{(i)} x(i)
- 确定输出单元的个数,即有几个类别。
- 一般来说,隐藏层的层数我们会选1层,如果大于一层,则令每层的单元数相同。
训练神经网络
- 随机初始化 θ \theta θ.
- 应用向前传播计算出每个 x ( i ) x^{(i)} x(i)对应的 h θ ( x ( i ) ) h_{\theta}(x^{(i)}) hθ(x(i)).
- 计算出代价函数 J ( θ ) J(\theta) J(θ).
- 应用反向传播计算出每个偏导数项 ∂ ∂ θ j k ( l ) J ( θ ) \frac{∂}{∂\theta_{jk}^{(l)}}J(\theta) ∂θjk(l)∂J(θ).
- 使用梯度检测将用反向传播求出的偏导项和用数值求出的偏导项进行比较.
- 利用优化算法求出最小化代价函数对应的参数 θ \theta θ.
吴恩达机器学习练习4
import numpy as np
import matplotlib.pyplot as plt
import scipy.optimize as opt
import matplotlib
from scipy.io import loadmat
from sklearn.metrics import classification_report
画几张图看看
def load_data(transpose=True):
data = loadmat('E:\\happy\\ML&DL\\My_exercise\\ex4-neural network\\ex4data1')
y = data.get('y') # (5000,1)
X = data.get('X') # (5000,400)
if transpose:
# 按行遍历,先转置得到一个正确的向量,再重新展开,否则画出来的图片会倒过来
X = np.array([image.reshape((20, 20)).T for image in X])
X = np.array([image.reshape(400) for image in X])
return X, y
题目中说到,每个训练样本有400个特征值,这400个特征值是通过一个手写数字转化为一个20×20的像素矩阵,再展开得到的,要还原这个手写数字,我们要先把每一行的特征值压缩成一个20×20的矩阵,在利用matshow函数画出来。
#画100张图
def plot_image(X):
size = int(np.sqrt(X.shape[1]))
# 随机选100个训练样本
index = np.random.choice(np.arange(X.shape[0]), 100) # 100*400
sample_images = X[index, :]
fig, ax_array = plt.subplots(nrows=10, ncols=10, sharey=True, sharex=True, figsize=(8, 8))
for r in range(10):
for c in range(10):
ax_array[r, c].matshow(sample_images[10 * r + c].reshape((size, size)),
cmap=matplotlib.cm.binary)
plt.xticks(np.array([]))
plt.yticks(np.array([]))
X, y = load_data()
plot_image(X)
数据处理
data = loadmat('E:\\happy\\ML&DL\\My_exercise\\ex4-neural network\\ex4data1')
data
X = data['X']
y = data['y']
X.shape,y.shape
下面我们用OneHotEncoder将y的1-10进行重新编码,用0和1表示,该函数的具体说明链接放在这里,如果你感兴趣的话可以去看看这篇文章哦。
https://www.cnblogs.com/zhoukui/p/9159909.html
from sklearn.preprocessing import OneHotEncoder
enc = OneHotEncoder()
enc.fit(y)
y_onehot = enc.transform(y).toarray()
y_onehot
y_onehot.shape
![]()
模型表示
我们用到的神经网络有三层,第一层是输入层,有400个单元(不包含偏置单元),第二层为隐藏层,有25个单元(不包含偏置单元),第三层是输出层,有10个单元。其中权重矩阵分别是一个25×401和10×26的矩阵。
#将矩阵重塑为(25, 401)和(10, 26)的矩阵
def deserialize(seq):
return seq[:25 * 401].reshape(25, 401), seq[25 * 401:].reshape(10, 26)
#读取权重矩阵
theta = loadmat('E:\\happy\\ML&DL\\My_exercise\\ex4-neural network\\ex4weights')
#将权重矩阵扁平化
theta = np.concatenate((np.ravel(theta['Theta1']), np.ravel(theta['Theta2'])))
#digmoid函数
def sigmoid(z):
return 1 / (1 + np.exp(-z))
#向前传播
def feed_forward(theta, X):
theta1, theta2 = deserialize(theta)
theta1 = np.matrix(theta1)
theta2 = np.matrix(theta2)
X = np.matrix(X)
a1 = np.insert(X, 0, values = np.ones(X.shape[0]), axis = 1)
z2 = a1 * theta1.T
a2 = np.insert(sigmoid(z2), 0, values = np.ones(X.shape[0]), axis = 1)
z3 = a2 * theta2.T
h = sigmoid(z3)
return a1, z2, a2, z3, h
#代价函数
def cost(theta, X, y):
m = X.shape[0]
_, _, _, _, h = feed_forward(theta, X)
y = np.matrix(y)
return np.sum(-np.multiply(y, np.log(h)) - np.multiply((1 - y), np.log(1 - h))) / m
cost(theta, X, y_onehot)
#正规化代价函数
def reg_cost(theta, X, y, lam=1):
m = X.shape[0]
theta1, theta2 = deserialize(theta)
#不计算第一列
reg_theta1 = np.sum(np.power(theta1[:, 1:], 2)) * (float(lam) / (2 * m))
reg_theta2 = np.sum(np.power(theta2[:, 1:], 2)) * (float(lam) / (2 * m))
return cost(theta, X, y) + reg_theta1 + reg_theta2
reg_cost(theta, X, y_onehot)
反向传播
由于参数矩阵已经知道,我们只要求出每一层sigmoid函数的梯度即可求出对应层的误差项
sigmoid函数梯度
g ′ ( z ( 2 ) ) = a ( 2 ) . ∗ ( 1 − a ( 2 ) ) g^{'}(z^{(2)})=a^{(2)}.*(1-a^{(2)}) g′(z(2))=a(2).∗(1−a(2))
#sigmoid函数的梯度
def sigmoid_gradient(z):
return np.multiply(sigmoid(z), (1 - sigmoid(z)))
下面来正式实现反向传播算法,首先将所有误差项△置0
然后不断循环累加,最终求出偏导。
跳出循环后,我们再计算以下式子:
这里的 D i j ( l ) D^{(l)}_{ij} Dij(l)就是代价函数关于每个参数的偏导了。
def reg_gradient(theta, X, y, lam=1):
theta1, theta2 = deserialize(theta)
theta1 = np.matrix(theta1)
theta2 = np.matrix(theta2)
X = np.matrix(X)
y = np.matrix(y)
m = X.shape[0]
#误差项初始化为0
delta1 = np.zeros(theta1.shape) #(25, 401)
delta2 = np.zeros(theta2.shape) #(10, 26)
#向前传播
a1, z2, a2, z3, h = feed_forward(theta, X)
#反向传播
for i in range(m):
a1i = a1[i,:] #(1, 401)
z2i = z2[i,:] #(1, 25)
a2i = a2[i,:] #(1, 26)
hi = h[i,:] #(1, 10)
yi = y[i,:] #(1, 10)
d3i = hi - yi #(1, 10)
z2i = np.insert(z2i, 0, np.ones(1)) #(1, 26)
d2i = np.multiply((theta2.T * d3i.T).T, sigmoid_gradient(z2i))
delta1 = delta1 + (d2i[:,1:]).T * a1i
delta2 = delta2 + d3i.T * a2i
delta1 = delta1 / m
delta2 = delta2 / m
#加入正规项
delta1[:,1:] = delta1[:,1:] + (theta1[:,1:] * lam) / m
delta2[:,1:] = delta2[:,1:] + (theta2[:,1:] * lam) / m
#将导数项展开成1行
grad = np.concatenate((np.ravel(delta1), np.ravel(delta2)))
return grad
grad= reg_gradient(theta, X, y_onehot)
grad.shape
![]()
利用scipy最小化函数
def random_init(size):
return np.random.uniform(-0.12, 0.12, size)
init_theta = random_init(10285)
res = opt.minimize(fun=reg_cost, x0=init_theta, args=(X, y_onehot),
method='TNC', jac=reg_gradient,options={'maxiter':400})
res
#预测
_, _, _, _, h = feed_forward(res.x, X)
y_pred = np.array(np.argmax(h, axis=1) + 1) #返回最大值的索引值+1
y_pred
#准确率
Accuracy = np.mean([1 if a == b else 0 for (a, b) in zip(y_pred, y)])
print('Accuracy = {}%'.format(Accuracy * 100))
![]()
源文件领取
关注公众号“大拨鼠Code”,回复“机器学习”可领取上面例题的源文件,jupyter版本的,例题和数据也一起打包了,之前的练习也在里面,感谢支持。
参考资料:
[1] https://www.bilibili.com/video/BV164411b7dx
[2] https://github.com/fengdu78/Coursera-ML-AndrewNg-Notes
[3] https://www.cnblogs.com/zhoukui/p/9159909.html