多元线性回归：波士顿房价预测问题TesnsorFlow实战

慕课：《深度学习应用开发-TensorFlow实践》
章节：第六讲 多元线性回归：波士顿房价预测问题TesnsorFlow实战
TensorFlow版本为2.3

问题介绍

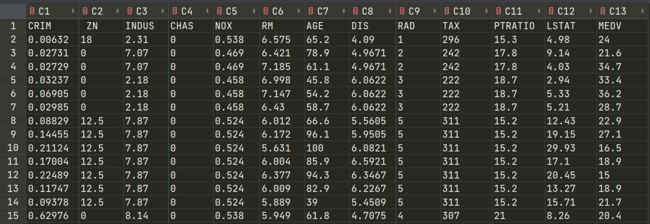
波士顿房价数据集包括506个样本，每个样本包括12个特征变量和该地区的平均房价房价（单价），显然和多个特征变量相关，不是单变量线性回归（一元线性回归）问题。选择多个特征变量来建立线性方程，这就是多变量线性回归（多元线性回归）问题

数据集介绍

数据集放在下面链接了，也可以去慕课上下
链接：https://pan.baidu.com/s/1CYTQSYUNi4U04i26wLYR9w
提取码：ymfa

简单看一下数据集

各个参数的含义

• CRIM: 城镇人均犯罪率
• ZN：住宅用地超过 25000 sq.ft. 的比例
• INDUS: 城镇非零售商用土地的比例
• CHAS: 边界是河流为1，否则0
• NOX: 一氧化氮浓度
• RM: 住宅平均房间数
• AGE: 1940年之前建成的自用房屋比例
• DIS：到波士顿5个中心区域的加权距离
• RAD: 辐射性公路的靠近指数
• TAX: 每10000美元的全值财产税率
• PTRATIO: 城镇师生比例
• LSTAT: 人口中地位低下者的比例
• MEDV: 自住房的平均房价，单位：千美元

接下来，代码走起来！！

数据处理

数据读取

首先，下载数据集，然后把csv文件和你的python文件放在同一个目录下，下面的代码里，一些显而易见的注释就不写了哈
第一步还是常规的导入包

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import pandas as pd
from sklearn.utils import shuffle
from sklearn.preprocessing import scale#导入sklearn的相关包
print(tf.__version__)

这里用到了两个新的库：pandas和sklearn，所以呢，如果出现了下面这些报错

不要慌，pandas没装，打开终端，进入环境，下面代码跑一跑

pip install pandas

10.2MB，可能还有一丢丢的慢，怎么办？换个源，走起

pip install pandas -i  https://pypi.doubanio.com/simple/

接着几秒之后就好了。
顺带的，动动手指把sklearn也装了，自己看网络，下面俩选一个

pip install sklearn
或者
pip install sklearn -i  https://pypi.doubanio.com/simple/

装完回来，就发现它好了

接下来，数据集保存在CSV文件中，所以我们这里用pandas库去读取相应的数据，至于pandas，这里就不介绍了，自行百度教程吧，用到的也不多，其实就一两个方法

df = pd.read_csv("boston.csv",header=0)

它读入的是pandas.core.frame.DataFrame类型，但是我们后面要处理他，所以要把它转换成我们所需要的np.array类型才可以，我们可以获取它对应的values值来实现我们要的效果，顺带看一下规格

df=df.values#返回np.array
df.shape

输出

(506, 13)

分离特征和标签

在数据集里面，前十二列是特征值，最后一列是标签，我们需要把它们分隔开来

x_data=df[:,:12]
y_data=df[:,12]
print(f"x_data shape:{x_data.shape},y_data shape:{y_data.shape}")

输出

x_data shape:(506, 12),y_data shape:(506,)

归一化操作，在上面那一段代码后面加一个for循环，如果不做这一步，后果会在后面的训练部分讲到

for i in range(12):
    x_data[:,i]=(x_data[:,i]-x_data[:,i].min())/(x_data[:,i].max()-x_data[:,i].min())

划分训练集、验证集和测试集

为啥要划分数据集呢？

构建和训练机器学习模型是希望对新的数据做出良好预测。那么，如果我们将所有的数据都去用于训练，这就好像我们考试前给你一份题库，并且告诉你所有考试题目都从上面出，一个字都不带改的，那么只要好好看过了，这不人均90+？
机器也是这样，你将所有数据都给它训练，那么他在这个数据集上的效果就会非常的好，但如果给它一份新的数据，那么效果就不得而知了。
既然如此，我们就把数据集划分一下，只给它一部分用来训练，测试的时候就可以给他新的数据了

一般而言，我们会将一个数据集划分成训练集和测试集

• 训练集 - 用于训练模型的子集
• 测试集 - 用于测试模型的子集

在测试集上表现是否良好是衡量能否在新数据上表现良好的有用指标，前提是：测试集足够大、不会反复使用相同的测试集来作假
此外，要确保测试集满足以下两个条件：

• 规模足够大，可产生具有统计意义的结果
• 能代表整个数据集，测试集的特征应该与训练集的特征相同

差不多流程就是这个样子的

不过这里有个问题，在每次迭代时，都会对训练数据进行训练并评估测试数据，并以基于测试数据的评估结果为指导来选择和更改各种模型超参数，那么…多次重复执行该流程可能导致模型不知不觉地拟合了特定测试集的特性
怎么办呢？

简单，再划分一个验证集出来，让验证集来进行上面流程中测试集的任务，而测试集只在最后测试一次，确保测试集机器只看到一次，然后工作流程就变成了这样
ok，原理讲完，代码走起

train_num=300# 训练集数量
valid_num=100# 验证集数量
test_num=len(x_data)-train_num-valid_num# 测试集数量

# 训练集划分
x_train=x_data[:train_num]
y_train=y_data[:train_num]

# 验证集划分
x_valid=x_data[train_num:train_num+valid_num]
y_valid=y_data[train_num:train_num+valid_num]

# 测试集划分
x_test=x_data[train_num+valid_num:train_num+valid_num+test_num]
y_test=y_data[train_num+valid_num:train_num+valid_num+test_num]

由于我们之后要将数据放入模型中训练、计算损失啥的，所以我们这里把它转换成tf.float32

x_train=tf.cast(x_train,dtype=tf.float32)
x_valid=tf.cast(x_valid,dtype=tf.float32)
x_test=tf.cast(x_test,dtype=tf.float32)

构建模型

定义模型

模型其实和我们上次一次做的单变量线性回归是一毛一样的，只不过这里的w和b不再是一个标量，而是一个矩阵罢了

def model(x,w,b):
    return tf.matmul(x,w)+b

创建变量

w=tf.Variable(tf.random.normal([12,1],mean=0.0,stddev=1.0,dtype=tf.float32))
b=tf.Variable(tf.zeros(1),dtype=tf.float32)
print(w,b)

训练模型

设置超参数

training_epochs=50
lr=0.001
batch_size=10

定义均方差损失函数

def loss(x,y,w,b):
    err=model(x,w,b)-y#计算预测值和真实值之间的差异
    squarred_err=tf.square(err)#求平方，得出方差
    return tf.reduce_mean(squarred_err)#求均值，得出均方差

定义梯度计算函数

def grad(x,y,w,b):
    with tf.GradientTape() as tape:
        loss_=loss(x,y,w,b)
    return tape.gradient(loss_,[w,b])# 返回梯度向量

选择优化器

这里我们选择了预制的一个SGD优化器

optimizer=tf.keras.optimizers.SGD(lr)

迭代训练

接下来就是训练的过程了

loss_list_train=[]#train loss
loss_list_valid=[]#val loss
total_step=int(train_num/batch_size)

for epoch in range(training_epochs):
    for step in range(total_step):
        xs=x_train[step*batch_size:(step+1)*batch_size,:]
        ys=y_train[step*batch_size:(step+1)*batch_size]
        grads=grad(xs,ys,w,b)#计算梯度
        optimizer.apply_gradients(zip(grads,[w,b]))#优化器调参
    loss_train=loss(x_train,y_train,w,b).numpy()
    loss_valid=loss(x_valid,y_valid,w,b).numpy()
    loss_list_train.append(loss_train)
    loss_list_valid.append(loss_valid)
    print(f"epoch={epoch+1},train_loss={loss_train},valid_loss={loss_valid}")

但是，你如果将数据直接就开始这样训练，那么就会出现下面这样的输出

epoch=1,train_loss=nan,valid_loss=nan
epoch=2,train_loss=nan,valid_loss=nan
epoch=3,train_loss=nan,valid_loss=nan
epoch=4,train_loss=nan,valid_loss=nan
epoch=5,train_loss=nan,valid_loss=nan
epoch=6,train_loss=nan,valid_loss=nan
epoch=7,train_loss=nan,valid_loss=nan
epoch=8,train_loss=nan,valid_loss=nan
epoch=9,train_loss=nan,valid_loss=nan
epoch=10,train_loss=nan,valid_loss=nan
epoch=11,train_loss=nan,valid_loss=nan
epoch=12,train_loss=nan,valid_loss=nan
epoch=13,train_loss=nan,valid_loss=nan
epoch=14,train_loss=nan,valid_loss=nan
epoch=15,train_loss=nan,valid_loss=nan
epoch=16,train_loss=nan,valid_loss=nan
epoch=17,train_loss=nan,valid_loss=nan
epoch=18,train_loss=nan,valid_loss=nan
epoch=19,train_loss=nan,valid_loss=nan
epoch=20,train_loss=nan,valid_loss=nan
epoch=21,train_loss=nan,valid_loss=nan
epoch=22,train_loss=nan,valid_loss=nan
epoch=23,train_loss=nan,valid_loss=nan
epoch=24,train_loss=nan,valid_loss=nan
epoch=25,train_loss=nan,valid_loss=nan
epoch=26,train_loss=nan,valid_loss=nan
epoch=27,train_loss=nan,valid_loss=nan
epoch=28,train_loss=nan,valid_loss=nan
epoch=29,train_loss=nan,valid_loss=nan
epoch=30,train_loss=nan,valid_loss=nan
epoch=31,train_loss=nan,valid_loss=nan
epoch=32,train_loss=nan,valid_loss=nan
epoch=33,train_loss=nan,valid_loss=nan
epoch=34,train_loss=nan,valid_loss=nan
epoch=35,train_loss=nan,valid_loss=nan
epoch=36,train_loss=nan,valid_loss=nan
epoch=37,train_loss=nan,valid_loss=nan
epoch=38,train_loss=nan,valid_loss=nan
epoch=39,train_loss=nan,valid_loss=nan
epoch=40,train_loss=nan,valid_loss=nan
epoch=41,train_loss=nan,valid_loss=nan
epoch=42,train_loss=nan,valid_loss=nan
epoch=43,train_loss=nan,valid_loss=nan
epoch=44,train_loss=nan,valid_loss=nan
epoch=45,train_loss=nan,valid_loss=nan
epoch=46,train_loss=nan,valid_loss=nan
epoch=47,train_loss=nan,valid_loss=nan
epoch=48,train_loss=nan,valid_loss=nan
epoch=49,train_loss=nan,valid_loss=nan
epoch=50,train_loss=nan,valid_loss=nan

可以看到，loss输出都是nan，他的原因就是输出太大了，那么我们要避免这个问题就需要对数据进行一定的标准化，因此，在这里我们要对数据做一个归一化操作，归一化测操作我在分离特征和标签这个步骤里已经写了，归一化之后，再重新运行，就好了

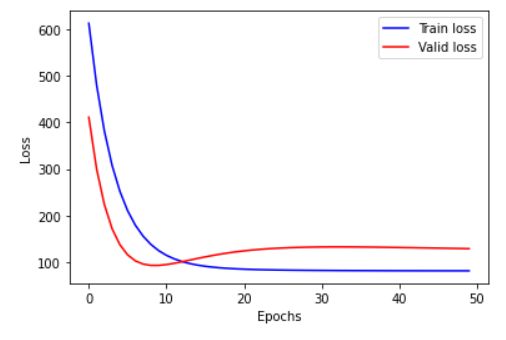
epoch=1,train_loss=611.9638061523438,valid_loss=410.65576171875
epoch=2,train_loss=480.1791076660156,valid_loss=300.2012634277344
epoch=3,train_loss=381.4595642089844,valid_loss=223.76609802246094
epoch=4,train_loss=307.4804992675781,valid_loss=171.88424682617188
epoch=5,train_loss=252.01597595214844,valid_loss=137.6017303466797
epoch=6,train_loss=210.4091796875,valid_loss=115.82573699951172
epoch=7,train_loss=179.17657470703125,valid_loss=102.8398666381836
epoch=8,train_loss=155.71231079101562,valid_loss=95.94418334960938
epoch=9,train_loss=138.06668090820312,valid_loss=93.18765258789062
epoch=10,train_loss=124.78082275390625,valid_loss=93.16976165771484
epoch=11,train_loss=114.76297760009766,valid_loss=94.89347839355469
epoch=12,train_loss=107.19605255126953,valid_loss=97.6563949584961
epoch=13,train_loss=101.46824645996094,valid_loss=100.97039031982422
epoch=14,train_loss=97.12144470214844,valid_loss=104.50247192382812
epoch=15,train_loss=93.81257629394531,valid_loss=108.03101348876953
epoch=16,train_loss=91.28462982177734,valid_loss=111.41390991210938
epoch=17,train_loss=89.34487915039062,valid_loss=114.56527709960938
epoch=18,train_loss=87.84889221191406,valid_loss=117.43827819824219
epoch=19,train_loss=86.68826293945312,valid_loss=120.01301574707031
epoch=20,train_loss=85.78163146972656,valid_loss=122.2874755859375
epoch=21,train_loss=85.06792449951172,valid_loss=124.2712631225586
epoch=22,train_loss=84.50117492675781,valid_loss=125.98110961914062
epoch=23,train_loss=84.04681396484375,valid_loss=127.43778991699219
epoch=24,train_loss=83.67878723144531,valid_loss=128.66384887695312
epoch=25,train_loss=83.3774642944336,valid_loss=129.68228149414062
epoch=26,train_loss=83.12799072265625,valid_loss=130.5154571533203
epoch=27,train_loss=82.91910552978516,valid_loss=131.18463134765625
epoch=28,train_loss=82.74230194091797,valid_loss=131.70956420898438
epoch=29,train_loss=82.59107971191406,valid_loss=132.10824584960938
epoch=30,train_loss=82.46050262451172,valid_loss=132.39715576171875
epoch=31,train_loss=82.34676361083984,valid_loss=132.59092712402344
epoch=32,train_loss=82.24696350097656,valid_loss=132.70252990722656
epoch=33,train_loss=82.1588363647461,valid_loss=132.74366760253906
epoch=34,train_loss=82.08061981201172,valid_loss=132.72451782226562
epoch=35,train_loss=82.01095581054688,valid_loss=132.6539764404297
epoch=36,train_loss=81.94876861572266,valid_loss=132.53993225097656
epoch=37,train_loss=81.89318084716797,valid_loss=132.38919067382812
epoch=38,train_loss=81.84352111816406,valid_loss=132.2075958251953
epoch=39,train_loss=81.79922485351562,valid_loss=132.00039672851562
epoch=40,train_loss=81.75981140136719,valid_loss=131.7720489501953
epoch=41,train_loss=81.72492980957031,valid_loss=131.52635192871094
epoch=42,train_loss=81.69425201416016,valid_loss=131.26663208007812
epoch=43,train_loss=81.66749572753906,valid_loss=130.99574279785156
epoch=44,train_loss=81.64443969726562,valid_loss=130.71609497070312
epoch=45,train_loss=81.6248779296875,valid_loss=130.42990112304688
epoch=46,train_loss=81.6086196899414,valid_loss=130.1387939453125
epoch=47,train_loss=81.59551239013672,valid_loss=129.84445190429688
epoch=48,train_loss=81.58541107177734,valid_loss=129.5481414794922
epoch=49,train_loss=81.57818603515625,valid_loss=129.2509307861328
epoch=50,train_loss=81.5737075805664,valid_loss=128.953857421875

接下来我们可以可视化一下loss

plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.plot(loss_list_train,'blue',label="Train loss")
plt.plot(loss_list_valid,'red',label='Valid loss')
plt.legend(loc=1)

测试模型

查看测试集损失

print(f"Test_loss:{loss(x_test,y_test,w,b).numpy()}")

输出：

Test_loss:115.94937133789062

应用模型

测试集里随机选一条

# use model
test_house_id=np.random.randint(0,test_num)
y=y_test[test_house_id]
y_pred=model(x_test,w,b)[test_house_id]
y_predit=tf.reshape(y_pred,()).numpy()
print(f"House id {test_house_id} actual value {y} predicted value {y_predit}")

输出

House id 34 actual value 11.7 predicted value 23.49941062927246

到这里就算结束了，建议去看看慕课。

学习笔记，仅供参考，如有错误，敬请指正！