Sobolev空间-广义函数的概念（二）

Sobolev空间-广义函数的概念（二）

广义函数的提出源于对扩充微商定义以及傅里叶变换定义的需求，基于此，本文首先复习一下广义函数的起源和广义函数的相关概念，然后详细阐述一下广义函数的运算（广义微商、乘法、平移算子与反射算子）和扩充后傅里叶变换的定义。

1. 广义函数的提出

本节主要简单回顾一下Sobolev空间-从Delta函数到广义函数的内容，即Delta函数以及广义函数的起源与发展。

内容一：Delta函数的提出让人们认识到函数概念（从近代科学技术和数学本身要求来看）已不敷需要，从而产生扩充函数概念的要求。

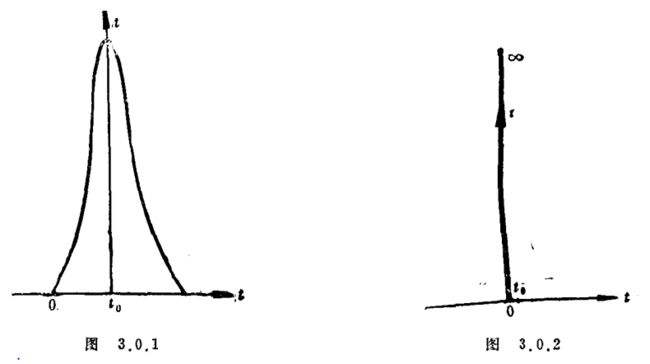
Delta函数的提出：工程师Heaviside在解电路方程时，提出了一种被称为算子演算（运算微积）的运算方法，它对如下的Heaviside函数
$$Y(x)=\{\begin{array}{ll}1& (x⩾0)\\ 0& (x<0)\end{array}$$
求微商, 并把这微商记作$\delta (x)$。

• $Y(x)$不可微(在$x=0$点不连续), 因此$\delta (x)$不可能是函数。它除了作为一个记号进行形式演算外, 在数学上没有意义。
• 图3.0.1表示实际单位脉冲的电流$i$和时间$t$的关系图, 在$t=0$时接通电源; 在$t=t_0$时截断电源, 总电量：${\int }_{-\infty }^{\infty }i(t)dt=1$。
• 图3.0.2表示理想化了的瞬间单位脉冲（$\delta (x)$在实际中的意义），“单位”是指总电量为1，“瞬时”是指$t_0\to 0$。代表瞬时单位脉冲的电流符号$\delta (t)$实际上代表一串实际单位脉冲电流函数$i_n(t)$在某种意义下的极限。
  

Dirac符号的另一种理解：在微观世界中, 把可观测到的物质的状态用波函数来描述，最简单的波函数具有形式 ${\mathrm{e}}^{i\lambda z}(-\infty <$ $r<\infty ),\lambda$ 是实数。通常要老虑如下形式的积分$\frac{1}{2\pi }{\int }_{-\infty }^{\infty }{\mathrm{e}}^{\mathrm{i}\lambda x}dx$，
可以把它按下列方式来理解：
$$\begin{array}{rl}\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }{e}^{i\lambda x}dx& =\underset{n\to \infty }{\lim }\frac{1}{2\pi }{\int }_{-\infty }^n{e}^{i\lambda x}dx\\ & =\underset{n\to \infty }{\lim }\frac{1}{\pi }\frac{\sin n\lambda }{\lambda }.\end{array}$$
该极限不存在，但物理学家们认为这是前面所说的瞬时单位脉冲“函数", 记作$\delta (\lambda )$。

内容二：$\delta (t)$本身不是一个函数，然而Heaviside的算法还要求对$\delta (t)$求微商和作其它运算，那么这一切在数学上究竟应当怎样解释呢? 特别是它的一些运算法则推导的根据是什么呢?

思路：问题不仅在于要引进一些理想的函数，更重要的在于要使这些 “理想的函数” 能够比较自由地进行分析运算。特别是要使“理想的函数”全部在新的意义下可微, 微商后还是某个“理想的函数”。

广义微商的提出：在数学本身的发展中, 也时常要求冲破古典分析对一些基本运算(如求微商和Fourier变换等)使用范围所加的限制。苏联数学家С.Л. Соболев 为确定偏微分方程解的存在性和唯一性, 发现如果仅限在古典意义下来理解微商及其所对应的方程，会造成很多不必要的限制并且排斥了很多近代数学工具使用的可能性。因而推广了微商，引进了广义微商的概念，提出了广义函数的思源（为泛函分析应用到微分方程理论建立了桥梁）。

2. 广义函数的定义及性质

本节首先引入广义函数定义的空间：基本空间 $\mathcal{D}(\Omega )$，以此，给出了广义函数的定义及其等价定义，易知$f(x)\to f$是1-1对应关系，广义函数包含$\delta$函数，局部可积函数等，但不是所有函数都是广义函数，最后介绍广义函数的收敛性。

2.1 基本空间 $\mathcal{D}(\Omega )$

定义（支集）设$\Omega \subset {\mathbb{R}}^n$是一个开集, $u\in C(\bar{\Omega })$, 称集合
$$F=\{x\in \Omega \mid u(x)\ne 0\}$$
的闭包(关于$\Omega$)为$u$的关于$\Omega$的支集，记作$supp\mu$，即连续函数$u$的支集是在此集外$u$恒为0的相对$\mathrm{E}\Omega$的最小闭集。

定义（${\mathrm{C}}_0^k(\Omega )$）：对于整数$k⩾0$(可以是$\infty$), ${\mathrm{C}}_0^k(\Omega )$表示支集在$\Omega$内紧的全体${\mathrm{C}}^k(\bar{\Omega })$ 函数所组成的集合,
$$C_0^{\infty }(\Omega )\subset \cdots \subset C_0^{k+1}(\Omega )\subset C_0^k(\Omega )\subset \cdots \subset C_0^0(\Omega )$$

内容一：$C_0^{\infty }(\Omega )$非空，即$C_0^{\infty }(\Omega )$中的函数构造。

示例 令$C_n\triangleq {\left({\int }_{|x|<1}{e}^{-\frac{1}{1-|x{|}^2}}dx\right)}^{-1}$是一个仅依赖于维数的常数。设
$$j(x)\triangleq \{\begin{array}{ll}{C}_n{\mathrm{e}}^{-\frac{1}{1-|x{|}^2}}& (|x|<1),\\ 0& (|x|⩾1),\end{array}$$
那么$j(x)\in C_0^{\infty }\left({\mathbb{R}}^n\right)$，且${\int }_{{\mathbf{R}}^n}j(x)dx=1$。

由此可以构造出许多$C_0^{\infty }\left(R^n\right)$的函数,

命题（$C_0^{\infty }(\Omega )$中函数的构造） 设$u(x)$是一个可积函数，在$\Omega$的一个紧子集$K$外恒为0，$j_{\delta }(x)\triangleq \frac{1}{{\delta }^n}\cdot j\left(\frac{x}{\delta }\right)$，则当$\delta >0$足够小时，则函数
$$u_{\delta }(x)\triangleq {\int }_{\Omega }u(y)j_{\delta }(x-y)dy$$
属于$C_0^{\infty }(\Omega )$中的函数。

定理（$u_{\delta }(x)$的性质）若 $u\in C_0^k(\Omega )$, 则
$${\Vert u_{\delta }(x)-u(x)\Vert }_C^k(\bar{\Omega })\to 0(\delta \to 0)\text{. }$$

推论 如果$\mu$ 是 $\Omega$ 上的一个完全可加测度, 由
$${\int }_{\Omega }\phi d\mu =0\left(\forall \phi \in C_0^{\infty }(\Omega )\right)$$
便能推出
$${\int }_{\Omega }\phi d\mu =0\left(\forall \phi \in C_0^0(\Omega )\right)$$

内容二：基本空间$\mathcal{D}(\Omega )$的定义

定义（基本空间$\mathcal{D}(\Omega )$） 在集合$C_0^{\infty }(\Omega )$上定义收敛性如下: 称序列$\left\{{\phi }_j\right\}$收敛于${\phi }_0$, 如果

1. 存在一个相对于$\Omega$的紧集$K\subset \Omega$, 使得$\mathrm{supp}\left({\phi }_j\right)\subset K(j=0,1,2,\cdots )$;
2. 对于任意指标 $a=\left(a_1,\cdots ,a_n\right)$ 都有
   $$\underset{\mathbf{\beta }\in \mathbf{X}}{\max }\left|{\partial }^{\mathbf{a}}{\phi }_j(x)-{\partial }^{\mathbf{a}}{\phi }_0(x)\right|\to 0(j\to \infty )\text{. }$$
   带上述收敛性的线性空间$C_0^{\infty }(\Omega )$, 称为基本空间$\mathcal{D}(\Omega )$ 。

注释：我们只在$\mathcal{D}(\Omega )$上引进了收敛性, 并没有给定拓扑, 而上述收敛性不能由任何模, 甚至准模所导出。$\mathcal{D}(\Omega )$不是$B^{\ast }$空间!

命题（$\mathcal{D}(\Omega )$是序列完备的） 若${\left\{{\psi }_j\right\}}_0^{\infty }$ 是一个基本列, 它适合

1. $\exists$ 公共紧支集 $K$, 使 $\mathrm{supp}{\phi }_j\subset K;$
2. $\forall \epsilon >0,\forall a,\exists .\mathrm{V}=N(\epsilon ,a)\in \mathbf{N}$, 使得
   $$\underset{\epsilon \in K}{\max }\left|{\partial }^{\alpha }{\phi }_n(x)-{\partial }^{\alpha }{\phi }_m(x)\right|<\epsilon (\text{当}m,n>N)$$
   则必有 ${\phi }_0\in \mathcal{D}(\Omega )$, 使得${\phi }_j\to {\phi }_0(j\to \infty )$。

2.2 广义函数的定义与性质

本节主要给出以下两部分内容：

1. 广义函数的定义及其等价条件，$f(x)\to f$是1-1对应关系；
2. 广义函数包含$\delta$函数，局部可积函数等，但不是所有函数（例如普通的不可测的函数）都是广义函数。

内容一：广义函数的定义及其等价条件

定义（广义函数集合${\mathcal{D}}^{\prime }(\Omega )$） $\mathcal{D}(\Omega )$上的一切线性连续泛函都称为广义函数, 即广义函数是满足以下条件的泛函$f:\mathcal{D}(\Omega )\to {\mathbb{R}}^1$，

1. 线性:
   $$\begin{array}{rl}& ⟨f,{\lambda }_1{\phi }_1+{\lambda }_2{\phi }_2⟩={\lambda }_1⟨f,{\phi }_1⟩+{\lambda }_2⟨f,{\phi }_2⟩\\ & \left(\forall {\phi }_1,{\phi }_2\in \mathcal{D}(\Omega ),\forall {\lambda }_1,{\lambda }_2\in {\mathbb{R}}^1\right);\end{array}$$
2. 对于任意的 $\left\{{\phi }_j\right\}\subset \mathcal{D}(\Omega )$, 只要 ${\phi }_j\to {\phi }_0(\mathcal{D}(\Omega ))$, 都有
   $$⟨f,{\phi }_j⟩\to ⟨f,{\phi }_0⟩(j\to \infty )$$
   一切广义函数所组成的集合记作${\mathcal{D}}^{\prime }(\Omega )$ 。

定理(广义函数的等价定义) 为了 $f\in {\mathcal{D}}^{\prime }(\Omega )$, 必须且仅须对任意相对于$\Omega$的紧集$K$，存在着常数$C$及非负整数 $m$, 使得
$$|⟨f,\phi ⟩|⩽C\sum _{|\alpha |\le m}\underset{x\in K}{\sup }\left|{\partial }^a\phi (x)\right|\left(\forall \phi \in \mathcal{D}(\Omega ),{\mathrm{supp}}^{\phi }\subset K\right)$$

定理（$f(x)\to f$是1-1对应关系）若把几乎处处相等的局部可积函数不加区别, 则
$$f(x)\to f,\left(L_{loc}^1(\Omega )\to {\mathcal{D}}^{\prime }(\Omega )\right)$$
是1-1对应的。

证明: 要证明若$f\in L_{Loc}^1(\Omega )$，且${\int }_{\Omega }f\phi dx=0,(\forall \phi \in \mathcal{D}(\Omega ))$，则$f(x)=0$。这只要证任意球$B\left(x_0,\delta \right))\subset \Omega$，都有$f(x)=0$。为此考察函数
$$\tilde{f}(x)\triangleq \{\begin{array}{ll}\mathrm{sign}f(x)& \left(x\in B\left(x_0,\delta \right)\right)\\ 0& \left(x\bar{\in }B\left(x_0,\delta \right)\right)\end{array}$$

显然有 $\tilde{f}\in L^1(\Omega )$, 且在$\Omega$的一个紧集$B\left(x_0,\delta \right)$外为0。由于$C_0^{\infty }(\Omega )$在 $L^p(\Omega )$中稠密, $C_0^{\infty }(\Omega )$ 函数可以任意逼近这个函数, 即函数
$${\tilde{f}}_{\delta }(x)\triangleq {\int }_{\Omega }\tilde{f}(y)j_{\delta }(x-y)dy,$$
当 $\delta >0$ 足够小时, 有
$${\Vert {\tilde{f}}_{\delta }-\tilde{f}\Vert }_{L^1(\Omega )}\to 0(\delta \to 0),$$
且 ${\tilde{f}}_{\delta }\in \mathcal{D}(\Omega )$. 从而由Riesz定理和Lebesgue控制收敛定理，可得
$${\int }_{B(x_0,\delta )}|f(x)|dx={\int }_{\Omega }f(x)\tilde{f}(x)dx=\underset{{\delta }_i\to 0}{\lim }{\int }_{\Omega }f(x){\tilde{f}}_{{\delta }_i}(x)dx=0$$
其中$\left\{{\delta }_i\right\}$是使得 ${\tilde{f}}_{{\delta }_i}\to \tilde{f}(\mathrm{p}.\mathrm{p}.\text{于}\Omega )$ 的正数列。即得
$$f(x)=0\left(\mathrm{p}.\mathrm{p}.\text{于}B\left(x_0,\delta \right)\right)$$

内容二：广义函数包含$\delta$函数，局部可积函数等，但是不是所有的函数都是广义函数。

示例1（广义函数包含$\delta$函数）设 $\theta \in \Omega$, 定义
$$⟨\delta ,\phi ⟩=\phi (\theta )(\forall \phi \in \mathcal{D}(\Omega ))$$
显然$\delta$是线性的, 而且当 ${\phi }_j\to {\phi }_0(\mathcal{D})$ 时, 有
$$\left|{\phi }_j(\theta )-{\phi }_0(\theta )\right|\to 0(j\to \infty )$$
从而 $⟨\delta ,{\varphi }_j⟩={\phi }_j(\theta )\to {\phi }_0(\theta )=⟨\delta ,{\phi }_0⟩(j\to \infty )$，即$\delta$在$\mathcal{D}(\Omega )$上是连续的, 所以$\delta$是一个广义函数。

示例2：对任意多重指标$\alpha =\left(a_1,\cdots ,a_n\right)$, 定义
$$⟨{\delta }^{⟨\alpha ⟩},\phi ⟩=(-1{)}^{|\alpha |}\left({\partial }^{\alpha }\phi \right)(\theta ),(\forall \phi \in \mathcal{D}(\Omega ))$$
则${\delta }^{(a)}$也是一个广义函数。

示例3（广义函数是局部可积函数的推广）：设$f(x)$是$\Omega$上的一个局部可积函数, 即对于任意相对于$\Omega$的紧集$K$, 积分${\int }_K|f(x)|dx<\infty$，记作$f(x)\in L_{loc}^1(\Omega )$，那么$f(x)$对应着一个广义函数
$$⟨f,\phi ⟩={\int }_{\Omega }f(x)\phi (x)dx,(\forall \phi \in \mathcal{D}(\Omega ))$$

由此可知, 广义函数只是局部可积函数的推广。在这个意义上, 我们说每个局部可积函数都是一个广义函数，凡将一局部可积函数看成广义函数时, 都按这种方式定义。这种对应并非在上的, 也就是说${\mathcal{D}}^{\prime }(\Omega )$含有比$L_{loc}^1(\Omega )$更多的元素。因此, 我们才把${\mathcal{D}}^{\prime }(\Omega )$中的元素称为广义函数。

示例4 若$\mu$是$\Omega$上的一个完全可加测度, 则$⟨f,\phi ⟩={\int }_{\Omega }\phi (x)d\mu (x),(\forall \phi \in \mathcal{D}(\Omega ))$定义了一个广义函数。

示例5 若$\Omega =(0,1)$, 则$
\langle f, \varphi\rangle=\sum_{j=1}^{\infty} \varphi(j)(\frac{1}{j}),(\forall \varphi \in \mathscr{D}(\Omega))$是一个广义函数。

定理：不是所有函数都是广义函数，普通的不可测的函数不能看成是广义函数。

2.3 广义函数的收敛性

内容一：广义函数收敛性的定义

在${\mathcal{D}}^{\prime }(\Omega )$上可以规定加法与数乘;
$$\begin{array}{c}⟨\left({\lambda }_1{f}_1+{\lambda }_2{f}_2\right),\phi ⟩={\lambda }_1⟨f_1,\phi ⟩+{\lambda }_2⟨f_2,\phi ⟩\\ \left(\forall \phi \in \mathcal{D}(\Omega ),\forall {\lambda }_1,{\lambda }_2\in {\mathbf{R}}^1\right),\end{array}$$
从而${\mathcal{D}}^{\prime }(\Omega )$构成一个线性空间。

定义（弱$\ast$收敛） 称 $\left\{f_j\right\}\subset {\mathcal{D}}^{\prime }(\Omega )$ 收敛到$f_0\in {\mathcal{D}}^{\prime }(\Omega )$, 是指:
$$⟨f_j,\phi ⟩\to ⟨f_0,\phi ⟩(\forall \phi \in \mathcal{D}(\Omega ))\text{. }$$

内容二：广义函数收敛性的示例

广义函数意义下的收敛是十分弱的收敛，举例可得

示例1：在${\mathbb{R}}^1$，以下是一串$L_{Loc}^1\left({\mathbb{R}}^1\right)$函数
$$f_j(x)=\frac{\sin jx}{\pi x}(j=1,2,\cdots )$$
从而可以看成是广义函数列，有$f_j\to$ $\delta \left({\mathcal{D}}^{\prime }(\Omega )\right)$.

示例2：当$\delta \to 0$（$\delta >0$）时, $j_{\delta }$作为广义函数列（见2.1节）收敛到$\delta (x)\left({\mathcal{D}}^{\prime }\left({\mathbb{R}}^n\right)\right)$。
若用${\delta }_{x_0}$表示广义函数
$$⟨{\delta }_{x_0},\phi ⟩=\phi \left(x_0\right)\left(\forall \phi \in \mathcal{D}\left({\mathbb{R}}^n\right)\right),$$
则$j_{\delta }\left(x-x_0\right)\to {\delta }_{x_0}$。

示例3：设$f_j(x)$是$\Omega$上的一串局部可积函数列, 且对任意相对于$\Omega$的紧集$K$, 存在常数$M_k$, 使得
$$\left|f_j(x)\right|⩽M_k(\forall x\in K,j=0,1,2,\cdots ),$$
且 $f_j(x)\to f_0(x)(j\to \infty )(\mathrm{p}.\mathrm{p}.x\in \Omega )$; 则作为广义函数列$f_j$,
$$⟨f_j,\phi ⟩={\int }_0{f}_j(x)\phi (x)dx(j=0,1,2,\cdots ),$$
在广义函数意义下收敛到 $f_0$ 。

证：由Lebesgue 控制收敛定理直接得到。

示例4：设 $f_1(x)={\mathrm{e}}^{-\pi |x{|}^2}$, 令
$$f_j(x)=j^{-n/2}{f}_1(\sqrt{j}x)=j^{n/2}{\mathrm{e}}^{-j\pi |x{|}^2},(j=2,3,\cdots )$$
则有$⟨f_j,\phi ⟩\to ⟨\delta ,\phi ⟩,\left(\forall \phi \in \mathcal{D}\left({\mathbb{R}}^n\right)\right)$，其中$f_j$是函数$f_j(x)$所对应的广义函数 $(j=1,2,3,\cdots )$。

3. 广义函数的运算（广义微商等）

内容一：$\mathcal{D}(\Omega )$ 上的连续线性算子的定义

定义（连续） 称一个线性算子$A:\mathcal{D}(\Omega )\to \mathcal{D}(\Omega )$是连续的, 是指
$${\phi }_j\to \phi (\mathcal{D}(\Omega ))\Rightarrow A{\phi }_j\to A\phi (\mathcal{D}(\Omega ))$$

• 示例（微分算子）任意微分算子 ${\partial }^{\alpha }$ 是 $\mathcal{D}(\Omega )$ 上的连续线性算子。

• 示例（乘法算子）设$\psi \in C^{\infty }(\Omega )$, 由$\psi$决定一个乘法算子线性连续
  $$A:\phi \mapsto \psi \cdot \phi \left(\forall \phi \in C^{\infty }(\Omega )\right)$$

内容二：我们利用以下算子给出广义函数的各种运算：广义微商、乘法、平移算子与反射算子

定理（${\mathcal{D}}^{\prime }(\Omega )$上连续算子$A^{\ast }$）在${\mathcal{D}}^{\prime }(\Omega )$上定义算子$A^{\ast }$ 如下：
$$⟨A^{\ast }f,\phi ⟩=⟨f,A\phi ⟩\left(\forall \phi \in \mathcal{D}(\Omega ),\forall f\in {\mathcal{D}}^{\prime }(\Omega )\right)$$
那么$A^{\ast }:{\mathcal{D}}^{\prime }(\Omega )\to {\mathcal{D}}^{\prime }(\Omega )$是连续的。

证明：如果 $f_j\to$ $f(\mathcal{D}(\Omega ))$, 那么対$\forall \phi \in \mathcal{D}(\Omega )$, 有
$$⟨A^{\ast }{f}_j,\phi ⟩=⟨f_j,A\phi ⟩\to ⟨f,A\phi ⟩=⟨A\ast f,\phi ⟩;$$
即得 $A\ast f_j\to A\ast f$ 。

3.1 广义微商

内容一：广义微商的定义

定义(广义微商) 称${\tilde{\partial }}^a=(-1{)}^a{\left({\partial }^a\right)}^{\ast }$为$a$阶广义微商运算, 即$\forall f\in {\mathcal{D}}^{\prime }(\Omega )$,
$$⟨{\tilde{\partial }}^{a}f,\phi ⟩=(-1{)}^{|a|}⟨f,{\tilde{\partial }}^a\phi ⟩,(\forall \phi \in \mathcal{D}(\Omega ))$$

1. 广义函数对微商运算是封闭的, 即任意广义函数$f\in$ ${\mathcal{D}}^{\prime }(\Omega )$ 都可以作任意次广义微商。
2. 若 $\alpha ,\beta$是任意两个多重指标, 则${\tilde{\partial }}^{\alpha }\cdot {\tilde{\partial }}^{\beta }={\tilde{\partial }}^{\alpha +\beta }={\tilde{\partial }}^{\beta }\cdot {\tilde{\partial }}^{\alpha }$
3. 由${\tilde{\partial }}^a$ 的连续性,$
   f_{j} \rightarrow f_{0} \Rightarrow \tilde{\partial}^{\alpha} f_{j} \rightarrow \tilde{\partial}^{\alpha} f_{0} .
   $，可见广义微商与极限可交换。

内容二：广义微商的示例

示例（一阶广义微商）：若$f(x)\in C^1(\Omega )$，对应
$$⟨f,\phi ⟩={\int }_{\Omega }f(x)\phi (x)dx,(\forall \phi \in \mathcal{D}(\Omega ))$$
产生的广义函数$f$有广义微商${\tilde{\partial }}_{x_i}f$，即${\tilde{\partial }}^{\alpha }f,\alpha =\stackrel{i}{(0,\cdots ,0,1},0,...,0))$。

证明：$f(x)$有普通的微商${\partial }_{x_i}f$, ${\tilde{\partial }}_{x_i}f$是${\partial }_{x_i}f$对应的广义函数，因为
$$\begin{array}{rl}⟨{\tilde{\partial }}_{x_i}f,\phi ⟩& =-⟨f,{\partial }_{x_i,}\phi ⟩=-{\int }_{\Omega }f(x){\partial }_{x_i}\phi (x)dx\\ & ={\int }_{\Omega }{\partial }_{x_i}f(x)\phi (x)dx(\forall \phi \in \mathcal{D}(\Omega ))\end{array}$$

示例（广义微商为$\delta$函数）若
$$Y(x)=\{\begin{array}{ll}1& (x>0)\\ 0& (x⩽0)\end{array}$$
则 ${\partial }_{x}Y(x)=\delta (x)$。

示例 若 ${\delta }^{(\alpha )}$ 是2.2节例2引进的广义函数, 即对任意多重指标$\alpha =\left(a_1,\cdots ,a_n\right)$, 定义
$$⟨{\delta }^{⟨\alpha ⟩},\phi ⟩=(-1{)}^{|\alpha |}\left({\partial }^{\alpha }\phi \right)(\theta ),(\forall \phi \in \mathcal{D}(\Omega ))$$
则 ${\tilde{\partial }}^a\delta ={\delta }^{(a)}$。

示例 设 $\tilde{\Delta }={\tilde{\partial }}_{x_1}^2+\cdots +{\tilde{\partial }}_{s_n}^2$, 那么
$$\begin{array}{ll}\tilde{\Delta }|x{|}^{2-n}=(2-n){\Omega }_n\delta (x)& (n⩾3),\\ \tilde{\Delta }\ln |x|=2\pi \delta (x)& (n=2),\end{array}$$
其中${\Omega }_n$是${\mathbb{R}}^n$中单位球面的面积。

3.2 广义函数的乘法

内容一：广义函数乘法的定义

定义（广义函数的乘法）对于任意的 $\psi \in C^{\infty }(\Omega )$, 以及 $f\in {\mathcal{D}}^{\prime }(\Omega )$, 定义
$$⟨\psi f,\phi ⟩=⟨f,\psi \phi ⟩(\forall \phi \in \mathcal{D}(\Omega )),$$
即定义广义函数对$C^{\infty }(\Omega )$函数的乘法为$\mathcal{D}(\Omega )$上乘法算了的共轭算子。显然它也是连续算子。

• 一般不能定义两个广义函数的乘积, 特别是两个$\delta$函数相乘, 因其结果不再是广义函数。

内容二：广义函数乘法的示例

示例：
$$x^n{\tilde{\partial }}^m\delta (x)=\{\begin{array}{ll}(-1{)}^n\frac{m!}{(m-n)!}{\delta }^{(m-n)}(x)& (m⩾n),\\ 0& (m<n).\end{array}$$

容易看出, 当 $f\in L_{loc}^1(\Omega )$, 对 $\forall \psi \in C^{\infty }(\Omega ),\psi f$的通常定义与作为广义函数的定义是一致的。

3.3 平移算子与反射算子

内容一：平移算子的推广

定义（平移算子） $\forall x_0\in {\mathbb{R}}^n$, 定义 ${\tau }_{x_0}:\mathcal{D}\left({\mathbb{R}}^n\right)\to \mathcal{D}\left({\mathbb{R}}^n\right)$ 为
$$\left({\tau }_{x_0}\phi \right)(x)=\phi \left(x-x_0\right)\left(\forall \phi \in \mathcal{D}\left({\mathbb{R}}^n\right)\right)$$
称 ${\tau }_{x_0}$ 为平移算子。易见 ${\tau }_{x_0}\in \mathcal{L}\left(\mathcal{D}\left({\mathbb{R}}^n\right)\right)$

定义（平移算子的推广）$\forall x_0\in {\mathbb{R}}^n,{\tilde{\tau }}_{x_0}\triangleq {\left({\tau }_{-x_0}\right)}^{\ast }$，即对 $\forall f\in {\mathcal{D}}^{\prime }\left({\mathbb{R}}^n\right)$，有
$$⟨{\tilde{\tau }}_{x_0}f,\phi ⟩=⟨f,{\tau }_{-x_0}\phi ⟩=⟨f,\phi \left(x+x_0\right)⟩\left(\forall \phi \in \mathcal{D}\left({\mathbb{R}}^{\ast }\right)\right)$$
${\tilde{\tau }}_{x_0}$ 是平移算子的推广。

证明：若 $f(x)\in L_{loc}\left({\mathbb{R}}^n\right)$, 则对 $\forall x_0\in {\mathbb{R}}^n$，有
$$\begin{array}{rl}{\int }_{R^n}f& \left(x-x_0\right)\phi (x)dx={\int }_{{\mathbb{R}}^n}f(x)\phi \left(x+x_0\right)dx\\ =& ⟨f,{\tau }_{-x_0}\phi ⟩=⟨{\tilde{\tau }}_{x_0}f,\phi ⟩\left(\forall \phi \in \mathcal{D}\left({\mathbb{R}}^{\prime }\right)\right),\end{array}$$
即得 ${\tilde{\tau }}_{x_0}f=f\left(x-x_0\right)={\tau }_{x_0}f$。

内容二：反射算子的推广

定义（反射算子）$\sigma :\mathcal{D}\left({\mathbb{R}}^n\right)\to \mathcal{D}\left({\mathbb{R}}^n\right)$定义为
$$(\sigma \phi )(x)=\phi (-x)\left(\forall \phi \in {\mathbb{R}}^n\right),$$
称 $\sigma$ 为反射算子。易见 $\sigma \in \mathcal{L}\left(\mathcal{D}\left({\mathbb{R}}^{\ast }\right)\right)$ 。

定理（反射算子的推广） $\tilde{\sigma }\triangleq {\sigma }^{\ast }$，即对 $\forall f\in {\mathcal{D}}^{\prime }\left({\mathbb{R}}^n\right)$,
$$⟨\tilde{\sigma }f,\phi ⟩=⟨{\sigma }^{\ast }f,\phi ⟩=⟨f,\sigma \phi ⟩\left(\forall \phi \in \mathcal{D}\left({\mathbb{R}}^n\right)\right).$$
$\tilde{\sigma }$ 是反射算子的推广。

证明：若 $f(x)\in L_{loc}^1\left({\mathbb{R}}^n\right)$，有
$$\begin{array}{rl}{\int }_{{\mathbb{R}}^n}f(& -x)\phi (x)dx={\int }_{{\mathbb{R}}^n}f(x)\phi (-x)dx\\ =& ⟨f,\sigma \phi ⟩=⟨\tilde{\sigma }f,\phi ⟩\left(\forall \phi \in \mathcal{D}\left({\mathbb{R}}^n\right)\right),\end{array}$$
即得 $\tilde{\sigma }f=f(-x)=\sigma f$ 。