K-Means 聚类算法应用
K-Means 聚类
监督学习被用于解决分类和回归问题,而无监督学习主要是用于解决聚类问题。聚类,顾名思义就是将具有相似属性或特征的数据聚合在一起。聚类算法有很多,最简单和最常用的就算是 K-Means 算法了。
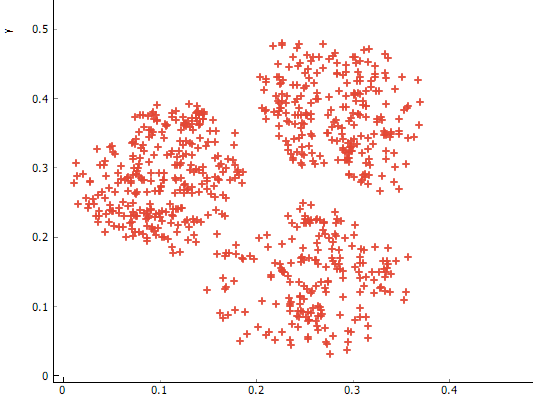
K-Means 算法在应用时,相对来上面的例子要复杂一些。现在,假设有如下图所示的一组二维数据。接下来,我们就一步一步演示 K-Means 的聚类过程。
首先,正如我们前面介绍无监督学习时所说,无监督学习面对的数据都是没有标签的。如果我们把下方示例数据的颜色看作是标签,那么只有一种颜色。
第一步,确定要聚为几类?也就是 K 值。假设,这里我们想将样本聚为 3 类。当然,你也完全可以将其聚为 2 类或 4 类,不要受到视觉上的误导。
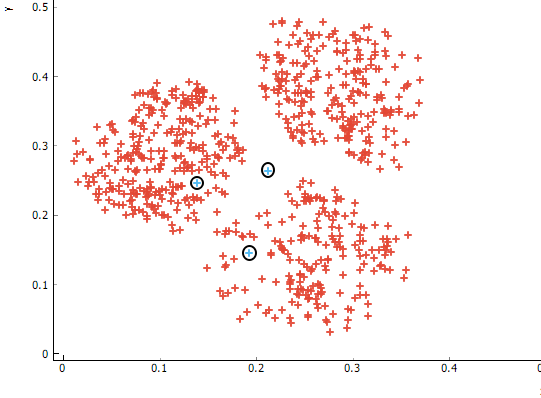
这里,我们以 3 类为例。当确定聚为 3 类之后,我们在特征空间上,随机初始化 3 个类别中心。这里的 3 也就对应着 K 值的大小。
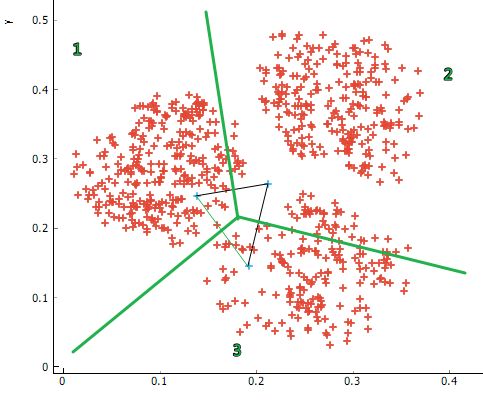
第二步,我们依据这三个随机初始化的中心,将现有样本按照与最近簇中心点之间的距离进行归类。图中绿线将全部样本划分为三个类别。(中间小三角形是参考线,可以忽略。)
这样,我们的样本被划为为三个区域。现在,我们就要用到上面提到的均值来重新求解 3 个区域对应的新的样本中心。
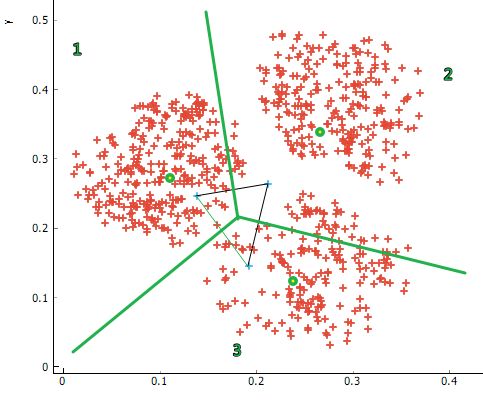
如上图所示,假设我们求解的新样本中心为三个绿点所示的位置。然后,又重新回到上一步,根据这三个中心重新划分样本,再求解中心。
依次迭代,直到样本中心变化非常小时终止。最终,就可以将全部样本聚类为三类。我们通过下面的动图来演示完整的 K-Means 的聚类过程。
https://doc.shiyanlou.com/courses/uid214893-20190523-1558591867573
让我们看一下 K-Means 如何在我们之前看过的简单数据集上运行。为了表示这是无监督的,我们将不绘制群集的颜色:
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs # 导入聚类数据生成器
%matplotlib inline
plt.style.use('seaborn') # 样式美化
# 生成 300 个可分成 4 类的数据
X, y = make_blobs(n_samples=300, centers=4,
random_state=0, cluster_std=0.60)
plt.scatter(X[:, 0], X[:, 1], s=50)
用肉眼看,挑选四个集群相对容易。但是,如果要对数据的不同分段执行详尽搜索,则搜索空间的点数将是指数级的,我们看看 K-Means 的聚类效果如何。接下来,导入 KMeans 估计器进行聚类。scikit-learn 中的聚类算法都包含在 sklearn.cluster 方法下,这里 KMeans 估计器最重要的参数就是 n_clusters,即我们选择聚类的类别数 k 值,完整的参数可参考 官方文档。
# 导入 KMeans 估计器
from sklearn.cluster import KMeans
est = KMeans(n_clusters=4) # 选择聚为 4 类
est.fit(X)
y_kmeans = est.predict(X) # 预测类别,输出为含0、1、2、3数字的数组
# 为预测结果上色并可视化
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis')
centers = est.cluster_centers_ # 找出中心
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.5) # 绘制中心点
该算法以与我们肉眼所见非常相似的方式识别四个点的聚类。
K均值算法:期望最大化
K-Means 是使用期望最大化方法得出结果的算法。期望最大化可解释成两步,其工作原理如下:
1.猜测一些簇中心点。
2.重复直至收敛。
期望步骤(E-step):将点分配至离其最近的簇中心点。
最大化步骤(M-step):将簇中心点设置为所有点坐标的平均值。
from sklearn.metrics import pairwise_distances_argmin # 最小距离函数
import numpy as np
def find_clusters(X, n_clusters, rseed=2):
# 1.随机选择簇中心点
rng = np.random.RandomState(rseed)
i = rng.permutation(X.shape[0])[:n_clusters]
centers = X[i]
while True:
# 2a.基于最近的中心指定标签
labels = pairwise_distances_argmin(X, centers)
# 2b.根据点的平均值找到新的中心
new_centers = np.array([X[labels == i].mean(0)
for i in range(n_clusters)])
# 2c.确认收敛
if np.all(centers == new_centers):
break
centers = new_centers
return centers, labels
centers, labels = find_clusters(X, 4)
plt.scatter(X[:, 0], X[:, 1], c=labels,
s=50, cmap='viridis') # 绘制聚类结果
上面是我们用期望最大化方法聚类出的结果,可以看到和我们直接用 K-Means 聚类是一样的。
K-Means在手写数字数据集中的应用
为了更加接近实际案例应用,让我们再次看一下手写数字数据集。在这里,我们将使用 K-Means 对 64 个维度的数据进行聚类,然后查看簇中心,观察其聚类效果。
from sklearn.datasets import load_digits # 导入数据集
digits = load_digits() # 加载数据集
est = KMeans(n_clusters=10) # 选择聚为 10 类
clusters = est.fit_predict(digits.data) # 返回每个数据对应的标签
est.cluster_centers_.shape # 输出簇中心参数
我们看到 64 个维度的 10 个群集。让我们可视化这些簇中心,看看它们代表什么:
fig = plt.figure(figsize=(8, 3)) # 创建画布,设置画布参数
for i in range(10):
ax = fig.add_subplot(2, 5, 1 + i, xticks=[], yticks=[]) # 创建子图
ax.imshow(est.cluster_centers_[i].reshape((8, 8)), cmap=plt.cm.binary)
我们看到,即使没有标签,K-Means 仍能找到 10 个簇的中心数字显示(数字 8 显示得不太明显)。聚类后的数据的标签的顺序按照类别排列了,我们先将其恢复到原来数据的顺序,再看看 K-Means 的准确性如何:
# scipy.stats.mode 寻找数组或者矩阵每行/每列中最常出现成员以及出现的次数
from scipy.stats import mode
from sklearn.metrics import accuracy_score # 导入评估模块
labels = np.zeros_like(clusters) # 变成全 0 数组
# 置换聚类后的数据标签顺序
for i in range(10):
mask = (clusters == i)
labels[mask] = mode(digits.target[mask])[0]
# 评估 K-Means 的准确性
accuracy_score(digits.target, labels)
可以看到准确性将近 80%,这个结果还是很不错的。
K-Means 用于色彩压缩
聚类的还有一种有趣的应用是用于彩色图像压缩。假设有一张具有数百万种颜色的图像(彩色图像中,每个像素的大小为 3 字节(RGB),可以表示的颜色总数为256×256×256),但其实大多数图像中的很大一部分色彩通常是不会被眼睛注意到的,而且图像中的很多像素都拥有类似或者相同的颜色。
通过数据集模块可以访问 scikit-learn 的许多图像。比如 load_sample_image 模块包含大量内置的图像,这里我们加载其中一张名为 'china' 的图片:
from sklearn.datasets import load_sample_image # 导入图像数据集
china = load_sample_image("china.jpg")
plt.imshow(china) # 图像显示
plt.grid(False) # 不显示网格线
china.shape
该图像存储在一个三维数组 (height, width, RGB) 中,以 0~255 的整数表示红 / 蓝 / 绿信息。我们将像素值缩小到 0 到 1 之间,然后将数组重塑为典型的 scikit-learn 输入 (n_samples,n_features):
X = (china / 255.0).reshape(-1, 3) # 指定新数组列为 3
print(X.shape)
我们现在使用 K-means 聚类,将 1600 万种颜色(256^3)缩减到 64 种颜色。这个原理是在数据中找到 Ncolor 个簇,并创建一个新图像,其中用最接近的簇的颜色替换真实的输入颜色,即一个簇(类)只有一种颜色。因为这里数据量较大,所以使用更加复杂的 MiniBatchKMeans 估计器。
# 导入 MiniBatchKMeans 估计器
from sklearn.cluster import MiniBatchKMeans
# 缩减到的颜色数量
n_colors = 64
X = (china / 255.0).reshape(-1, 3) # 重塑输入
model = MiniBatchKMeans(n_colors)
labels = model.fit_predict(X) # 返回每个数据对应的标签
colors = model.cluster_centers_ # 得到簇中心颜色
new_image = colors[labels].reshape(china.shape) # 新图像生成
new_image = (255 * new_image).astype(np.uint8) # 像素值恢复
# 绘制新图像
with plt.style.context('seaborn-white'): # 绘图风格
plt.figure()
plt.imshow(china)
plt.title('input: 16 million colors')
plt.figure()
plt.imshow(new_image)
plt.title('{0} colors'.format(n_colors))
我们比较上面两个图像输出,将颜色从 256 ^ 3种缩减到了 64 种,但最后成像差别不大,颜色数量的大幅减少可以提高模型运行速度,你还可以将上面代码中 n_colors 改为 8、16 或者 32,看看最后新图像效果。
K 值选择
前面我们举的例子的类别都是事先知道的,所以我们模型训练时的 K 值都是可知的,但面对分类不明确甚至基本完全不知其分布规律的数据,我们在进行聚类的 K 值要怎么选择呢?
有一种评估方法,叫 轮廓系数。轮廓系数综合了聚类后的两项因素:内聚度和分离度。内聚度就指一个样本在簇内的不相似度,而分离度就指一个样本在簇间的不相似度。
在 scikit-learn 中,同样也提供了直接计算轮廓系数的方法。我们使用实验一开始生成的可分成 4 类的简单数据集,绘制出轮廓系数与聚类 K 值变化的折线图。
from sklearn.metrics import silhouette_score # 导入轮廓系数计算模块
index2 = [] # 横坐标
silhouette = [] # 轮廓系数列表
# 生成 300 个可分成 4 类的数据
X, y = make_blobs(n_samples=300, centers=4,
random_state=0, cluster_std=0.60)
# K 从 2 ~ 10 聚类
for i in range(8):
est = KMeans(n_clusters=i + 2)
index2.append(i + 2)
silhouette.append(silhouette_score(X, est.fit_predict(X)))
print(silhouette) # 输出不同聚类下的轮廓系数s
# 绘制折线图
plt.plot(index2, silhouette, "-o")
轮廓系数越接近于 1,代表聚类的效果越好。我们可以很清楚的看出,K=4 对应的轮廓系数最大,也更接近于 1 。