PCA 主成分分析应用
主成分分析
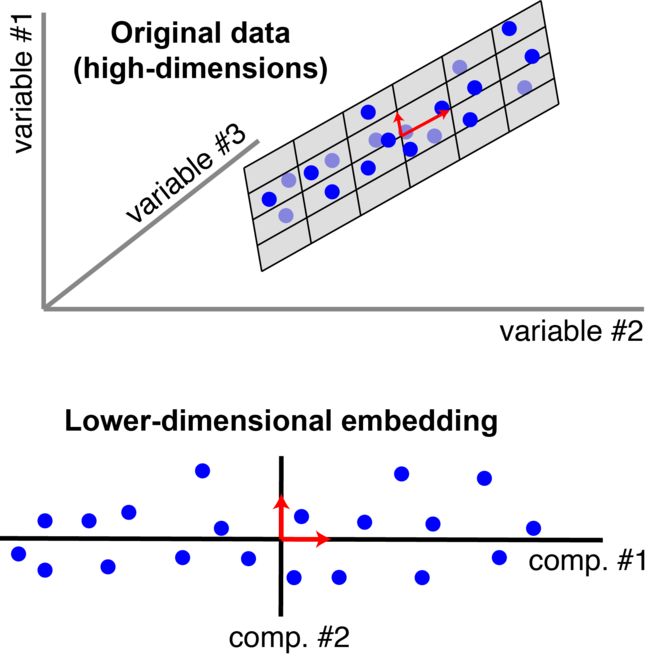
主成分分析 是多元线性统计里面的概念,它的英文是 Principal Components Analysis,简称 PCA。主成分分析旨在降低数据的维数,通过保留数据集中的主要成分来简化数据集。简化数据集在很多时候是非常必要的,因为复杂往往就意味着计算资源的大量消耗。通过对数据进行降维,我们就能在结果不受影响或受略微影响的同时,减少模型学习时间。
特别强调的是,本次实验所说的降维,不是指降低 NumPy 数组的维度,而是特指减少样本的特征数量。
上图展示了把三维空间的数据降维到二维空间的过程。
下面,介绍一下 scikit-learn 中 PCA 方法的参数定义及简单使用,这是完成 PCA 主成分分析的基础。
sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False, svd_solver='auto')
其中:
n_components= 表示需要保留主成分(特征)的数量。
copy= 表示针对原始数据降维还是针对原始数据副本降维。当参数为 False 时,降维后的原始数据会发生改变,这里默认为 True。
whiten= 白化表示将特征之间的相关性降低,并使得每个特征具有相同的方差。
svd_solver= 表示奇异值分解 SVD 的方法。有 4 个参数,分别是:auto, full, arpack, randomized。
我们生成一个最容易可视化降维过程的二维数据集来看下:
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
%matplotlib inline
plt.style.use('seaborn') # 样式美化
# 当我们设置相同的seed时,每次生成的随机数也相同,如果不设置seed,则每次生成的随机数都会不一样
np.random.seed(1)
X = np.dot(np.random.random(size=(2, 2)),
np.random.normal(size=(2, 200))).T # 生成二维数据
plt.plot(X[:, 0], X[:, 1], 'o')
plt.axis('equal')
我们可以看到数据有一个明确的趋势。PCA 要做的就是在数据中找到主轴,并解释这些轴在描述数据分布中的重要性:
# 导入 PCA 估计器
from sklearn.decomposition import PCA
pca = PCA(n_components=2) # 保留两个特征(维度)
pca.fit(X)
print(pca.explained_variance_)
print(pca.components_)
我们看到了两个输出,要了解这些数字的含义,让我们将其视为向量在数据点上绘制出来:
plt.plot(X[:, 0], X[:, 1], 'o', alpha=0.5)
for length, vector in zip(pca.explained_variance_, pca.components_):
v = vector * 3 * np.sqrt(length)
plt.plot([0, v[0]], [0, v[1]], '-k', lw=3) # lw设置线宽
plt.axis('equal')
绘图结果来看,一个向量比另一个向量长。从某种意义上讲,这告诉我们数据中的这个方向比另一个方向更“重要”,而这种方向上的“重要性”是用方差来量化的。当然这也告诉我们,在不损失大量信息的情况下完全可以忽略第二个主要成分。让我们看看如果仅保留 95%的方差,数据将是什么样子:
clf = PCA(0.95) # 保存 95%的方差
X_trans = clf.fit_transform(X)
print(X.shape)
print(X_trans.shape)
在使用 PCA 降维时,我们也会使用到 PCA.fit() 方法。.fit() 是 scikit-learn 训练模型的通用方法,但是该方法本身返回的是模型的参数。所以,通常我们会使用 PCA.fit_transform() 方法直接返回降维后的数据结果。
上面结果来看,通过舍弃 5%的方差,数据从 2 维变成了 1 维,相当于压缩了 50%。让我们看看压缩后的数据是什么样的:
# 将降维后的数据转换成原始数据的维度,才能绘图
X_new = clf.inverse_transform(X_trans)
plt.plot(X[:, 0], X[:, 1], 'o', alpha=0.2)
plt.plot(X_new[:, 0], X_new[:, 1], 'ob', alpha=0.8)
plt.axis('equal')
暗一点的是原始数据,而亮一点的是投影版本。我们看到将这个数据集的方差截断 5%再重新投影之后,数据“最重要”的功能得以保留,并且我们将数据压缩了 50%,这也就是降维的意义:如果可以在较低维度上得到近似数据集,则我们可以更轻松地查看它或将更复杂的模型拟合到数据中。
PCA 手写数字数据集应用
降维在二维数据上似乎表现得没有那么重要,但是在可视化高维数据时,投影和降维非常有用。让我们看一下 PCA 在我们之前看过的手写数字识别数据中的应用:
# 导入数据集模块
from sklearn.datasets import load_digits
digits = load_digits() # 载入数据集
X = digits.data
y = digits.target
pca = PCA(n_components=2) # 从 64 维降维到 2 维
Xproj = pca.fit_transform(X)
print(X.shape) # 查看原数据
print(Xproj.shape) # 查看降维后的数据
# 绘制降维后的数据散点图
plt.scatter(Xproj[:, 0], Xproj[:, 1], c=y, edgecolor='none', alpha=0.5,
cmap=plt.cm.get_cmap('nipy_spectral', 10))
plt.colorbar() # 绘制色标
我们将 64 维的数据降到了 2 维,并将其可视化绘制出来,这使我们对数字之间的关系有了一个概念,并且使我们无需参考标签即可查看数字的布局。
之前,我们用支持向量机完成了分类,即预测哪一张图像代表哪一个数字。现在,我们采用相同的数据集完成聚类分析,即将全部数据集聚为 10 个类别。
我们将降到 2 维后的数据聚为 10 类,并将聚类后的结果、聚类中心点、聚类决策边界绘制出来。
from sklearn.cluster import KMeans
pca = PCA(n_components=2) # 从 64 维降维到 2 维
Xproj = pca.fit_transform(X)
# 建立 K-Means 并输入数据
model = KMeans(n_clusters=10)
model.fit(Xproj)
# 计算聚类过程中的决策边界
x_min, x_max = Xproj[:, 0].min() - 1, Xproj[:, 0].max() + 1
y_min, y_max = Xproj[:, 1].min() - 1, Xproj[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, .05),
np.arange(y_min, y_max, .05)) # 生成网格点坐标矩阵
result = model.predict(np.c_[xx.ravel(), yy.ravel()])
# 绘制决策边界
result = result.reshape(xx.shape)
plt.figure(figsize=(10, 5))
plt.contourf(xx, yy, result, cmap=plt.cm.Greys) # 绘制填充色
plt.scatter(Xproj[:, 0], Xproj[:, 1], c=y, edgecolor='none', alpha=0.5,
cmap=plt.cm.get_cmap('nipy_spectral', 10)) # 绘制数据散点图
plt.colorbar() # 绘制色标
# 绘制聚类中心点
center = model.cluster_centers_
plt.scatter(center[:, 0], center[:, 1], marker='p',
linewidths=2, color='b', edgecolors='w', zorder=20)
# 图像参数设置
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
图中,不同的色块区域代表一类。这里色块的颜色没有意义,只表示类别。散点代表数据,散点的颜色表示数据原始类别。我们可以看出,虽然原始数据已经降到了 2 维,但某几个数字的依旧有明显的成团现象。
除此之外,我们还可以使用分类方法来对比降维前后的数据表现。我们使用随机森林方法对数据进行分类,并通过交叉验证得到准确度结果。
from sklearn.ensemble import RandomForestClassifier # 导入随机森林估计器
from sklearn.model_selection import cross_val_score # 导入交叉验证
model = RandomForestClassifier()
# 5 折交叉验证平均准确度
s1 = cross_val_score(model, X, y, cv=5).mean() # 原始维度数据
s2 = cross_val_score(model, Xproj, y, cv=5).mean() # 降维后的数据
print(s1)
print(s2)
你可以看到,实际上准确度并不是特别低。也就是说,在客观条件限制下,我们往往可以以更少维度的数据训练出准确度可以勉强接受的模型。
其他降维估计器
scikit-learn 还包含许多其他无监督学习的降维估计器,你可以尝试其他的降维方法:
sklearn.decomposition.IncrementalPCA:增量主成分分析(IPCA)
sklearn.decomposition.SparsePCA:PCA 变体,包括 L1 正则
sklearn.decomposition.FastICA:独立成分分析
sklearn.decomposition.NMF:非负矩阵分解
sklearn.manifold.LocallyLinearEmbedding:基于局部邻域几何的非线性流形学习
sklearn.manifold.IsoMap:基于稀疏图算法的非线性流形学习