算法题（二）

目录        
    1 左神部分集锦        
    2 Leetcode前150题        
    3 牛客网剑指offer        
    4 JavaG        
    5 题目中的细节处理 

2 Leetcode前150题

2.1 动态规划

通过金矿模型介绍动态规划 - 刘永辉 - 博客园

小结：

（1）通用步骤：定义dp数组意义->初始化边界条件->状态转移方程，通常采用迭代解题

（2） 一维dp数组初始化条件为dp[0]，二维dp数组初始化条件为矩阵的亮条边界（均为dp前进方向起点）

（3）遇到特殊条件，在初始化时也要特殊处理，在状态转移方程中也一般作为方程的分段条件

（4）可以应用动态规划求解的问题主要由四个特点：

        · 问题是求最优解

        · 整体问题的最优解依赖于各个子问题的最优解

        · 大问题分解成若干小问题，这些小问题之间还有相互重叠的更小的子问题

        · 从上往下分析问题，从下往上求解问题

2.1.1 code032 最长有效括号

    思路：dp[i]表示以i为子字符串末尾时的最大长度，最后的结果就是dp中的最大值。如果不是空字符串，则dp[0]=0，因为一个括号肯定无法正确匹配

（1）定义dp数组，长度同字符串长度

（2）定义起始条件，dp[0]

（3）遍历查找“)”，因为有效子串的最后结尾一定为")"

（4）往前找dp[i-1]的有效子串长度的前一个，看看是否为"("

（5）为"("则，当前dp值加2

（6）如果当前位置前还有有效子串，要加上其长度，如()(())，左边这对括号要加上长度

2.1.2 code053 最大子序和

（1）定义dp数组为对应下标时的最大和子数组，长度为数组长度

（2）定义起始条件，dp[0]

（3）遍历数组

        状态转移方程：

dp[i] =dp[i-1] + s[i] (dp[i-1] >=0)

dp[i] =s[i] (dp[i-1] <0)

2.1.3 code062 不同路径

（1）定义dp[m][n]数组代表此位置所有的路径个数

（2）初始化列边界，初始化行边界

（3）状态转移方程，上方和左边路径之和

2.1.4 code063 不同路径II

（1）定义dp[m][n]数组代表此位置所有的路径个数

（2）初始化列边界，初始化行边界，对边界的特殊情况处理

（3）状态转移方程，以obstacleGrid作为分段条件

2.1.5 code064 最小路径和

（1）定义dp[m][n]数组代表此位置的最小路径和

（2）初始化列边界，初始化行边界

（3）状态转移方程，取两个方向的最小值

2.1.6 code070 爬楼梯

（1）定义dp数组，长度为给定长度+1

（2）初始化边界条件

（3）状态转移方程,前1阶或者前2阶dp值之和

 这题用递归算法做也很简单，能看到递归转换为dp的模型。

2.1.7 code072编辑距离

（1）定义dp数组，分别为两个字符串长度 + 1，代表前i个操作符长度的最少操作数

        这里如果定义为字符串长度，对i = 0位置需要进行判断，定义为 length + 1可以简化逻辑。

（2）边界条件，其中一个字符串为空

（3）状态转移方程，判断在增加、删除、替换一个字符中，哪个是最少操作数

2.1.8 code087 扰乱字符串

    本题较难，如果使用DP算法，则需要使用三维dp

（1）定义三维dp数组：dp[k][i][j]表示s1(i。。。i+k)是否可以由s2(j。。。j+k)变化来

            ·第一维：子串的剩余长度

            ·第二维：s1的起始索引

            ·第三维：s2的起始索引

（2）初始化边界条件，子串剩余长度为0，代表只考虑当前字符

（3）状态转移方程：任意长度的字符串，把s1分为a1和b1,把s2分为a2和b2，则满足(a1~a2 && b1~b2)||(a1~b2 && a2~b1)

2.1.9 code091 解码方法

    本题难点在特殊条件的查找，如10、20分界线.

（1）定义dp数组，长度为字符串长度+1，dp[i]表示i长度时的解码方法

（2）初始化边界，空子串和一个字符时的解码方法

（3）a = Integer.valueOf(s.substring(i - 2, i))只看最后两位字符的解码

（4）状态转移方程

    · a > 10 && a <= 26 && s.charAt(i - 1) != '0'此范围时，两种解码方法AB --> A B, AB

    · a == 10 || a== 20这种情况，只能合并解码

    · 否则s.charAt(i - 1) != '0'时，只能分开解码

    · 其他情况无法解码

2.1.10 code096 不同的二叉搜索树

（1）定义dp数组，dp[i]表示1--i的数表示的BST数量

（2）初始化边界条件，空数，单节点，双节点

（3）状态转移方程

        Count[3] = Count[0]*Count[2] (1为根的情况) + Count[1]*Count[1] (2为根的情况) + Count[2]*Count[0] (3为根的情况)

 所以发现规律也很重要

2.1.11 code097 交错字符串

（1）定义dp数组，dp[i][j]表示s1为i长度，s2为j长度时，是否可以交错

（2）初始化空字符串情况，初始化边界，一个字符串为空，另一个字符串是否与s3相等

（3）状态转移方程，当前位置哪个字符串的值与s3相等，若相等并比较去掉当前字符串的情况

2.1.12 code115 不同的子序列

（1）定义dp数组,长度为字符串长度+1，dp[i][j]表示，当前下标的子序列出现个数

（2）初始化边界条件，当目标子序列为空时，子序列也唯一是空

（3）状态转移方程，当前字符相等，要么匹配要么跳过；当前字符不相等，只能跳过

2.1.13 code120 三角形最小路径和

（1）定义dp列表，并初始化为最底层列表

（2）状态转移方程，相邻的两个数中最小数与当前数相加

2.1.14 code121 买卖股票的最佳时机

（1）定义dp数组，dp[i]表示当前下标时的最大利润

（2）状态转移方程，取前一天利润和今天最大利润（减去之前最低价格）的最大值

2.1.15 code123 买卖股票的最佳时机III

思路：开辟两个数组f1和f2，f1[i]表示在price[i]之前进行一次交易所获得的最大利润，f2[i]表示在price[i]之后进行一次交易所获得的最大利润。则f1[i]+f2[i]的最大值就是所要求的最大值（代码中则是从后往前寻找降幅最大）

（1）定义dp1数组，dp1[i]表示在price[i]之前的最大利润

（2）状态转移方程

（3）定义dp2数组，dp2[i]表示在price[i]之前的最大利润

（4）状态转移方程

（5）遍历判断最大值

2.1.16 code132 分割回文串II

（1）定义一个缓存数组，isPal[i][j]表示字符串s(j,i+1)是否是回文串（优化性能）

（2）定义dp数组，dp[i]表示到当前下标时，所需要的最少切割次数

（3）边界初始化，i + 1的字符每次最多切i次就满足要求

（4）状态转移方程，如果一个字符串与尾部字符相同，且中间也是回文串，或者长度为1或者2，进而比较得到当前最小分割：之前最小与dp[j]之前的最小分割+1比较

2.1.17 code139 单词拆分

（1）定义dp数组,dp[i]表示到当前下标位置的字符串是否在列表中

（2）状态转移方程，当(j, i + 1)的子串匹配时，检测dp[j - 1]是否也满足

2.1.18 code140 单词拆分II

    动态规划+DFS

（1）与code139一样构造check方法，判断是否拆分有效

（2）dfs的终止条件：子串长度为0

（3）dfs分割

if(wordDict.contains(s.substring(0, i))) {

    dfs(s.substring(i, s.length()), wordDict, str + (str.equals("")? "" : " ") + s.substring(0, i));

}

2.1.19 Code005 最长回文子串

（1）定义dp数组   dp[i][j] 表示 s[i,j]是否是回文串

（2）边界条件初始化，i==j都为true

（3）遍历 字符串

（4）状态转移方程和边界条件 dp[i][j] = (s[i] == s[j]) and dp[i + 1][j - 1]

（5）如果两个下标对应字符串不相等，则dp[i][j] = false;

（6）如果相等，分类讨论。若i和j下标之间距离小于3，直接置为ture；否则，需要判断dp[i+1][j-1]是否是回文

（7）若i到j之间是回文，更新全局最大长度和记录当前起始下标

（8）返回最大长度子串

2.1.20 Code010 正则表达式匹配

思路：

（1）如果 p.charAt(j) == s.charAt(i) : dp[i][j] = dp[i-1][j-1]；

（2）如果 p.charAt(j) == '.' : dp[i][j] = dp[i-1][j-1]；

（3）如果 p.charAt(j) == '*'：

    · 如果 p.charAt(j-1) != s.charAt(i) : dp[i][j] = dp[i][j-2] //in this case, a* only counts as empty

    · 如果 p.charAt(i-1) == s.charAt(i) or p.charAt(i-1) == '.'：

        ·dp[i][j] = dp[i-1][j] //in this case, a* counts as multiple a

        ·or dp[i][j] = dp[i][j-1] // in this case, a* counts as single a

        ·or dp[i][j] = dp[i][j-2] // in this case, a* counts as empty

2.1.21 Code044 通配符匹配

（1）定义dp数组，dp[i][j] 表示字符串 s 的前 i 个字符和模式 p 的前 j 个字符是否能匹配

（2）初始化边界条件，s为空，p前面是否是连续的*

（3）状态转移方程

2.1.22 Code085 最大矩形

思路：

· 我们可以以常数时间计算出在给定的坐标结束的矩形的最大宽度。我们可以通过记录每一行中每一个方块连续的“1”的数量来实现这一点。每遍历完一行，就更新该点的最大可能宽度。通过以下代码即可实现。 row[i] = row[i - 1] + 1 if row[i] == '1'

· 一旦我们知道了每个点对应的最大宽度，我们就可以在线性时间内计算出以该点为右下角的最大矩形。当我们遍历列时，可知从初始点到当前点矩形的最大宽度，就是我们遇到的每个最大宽度的最小值

（1）定义dp数组，dp[i][j]表示以当前元素结尾的连续同行1的个数

（2）遍历二维数组

（3）若当前元素为1，进行运算

（4）状态转移方程 dp[i][j] = j == 0 ? 1 : dp[i][j - 1] + 1

（5）从当前行往上遍历

（6）找到所有行中的最小值

（7）更新最大面积变量

2.2 二叉树

    看到树的题，首先想到可能要用递归来解题。

小结：

（1）二叉树遍历

· 二叉树的前序、中序、后序遍历（深度优先遍历DFS） 

    遍历即将树的所有结点都访问且仅访问一次。按照根结点访问次序的不同，可以分为前序遍历，中序遍历，后序遍历。 

前序遍历：根结点 -> 左子树 -> 右子树  abdefgc 

中序遍历：左子树 -> 根结点 -> 右子树  debgfac 

后序遍历：左子树 -> 右子树 -> 根结点  edgfbca

图2-1 二叉树的遍历

· 层次遍历（广度优先遍历BFS） 

    层次遍历：abcdfeg

（2）有关于二叉搜索树的性质，可以多考虑使用中序遍历为升序来解题。

 一定要注意元素也不能相等。

2.2.1 Code105 从前序与中序遍历序列构造二叉树

（1）递归停止条件，树为空

（2）对特殊情况直接处理，只有根节点

（3）前序遍历的第一个元素为root节点

（4）在中序遍历中找到根节点,同时其下标index也是左子树节点个数

（5）对左右子树递归，根据前面得到的左子树长度index，划分两个数组进行递归

2.2.2 Code106 从中序与后序遍历序列构造二叉树

（1）递归停止条件，树为空

（2）对特殊情况直接处理，只有根节点

（3）后序遍历的最后一个元素为root节点

（4）在中序遍历中找到根节点,同时其下标index也是左子树节点个数

（5）对左右子树递归，根据前面得到的左子树长度index，划分两个数组进行递归

2.2.3 Code108 将有序数组转换为二叉搜索树

（1）递归停止条件, 数组长度为0

（2）取有序数组最中间的点作为根节点

（3）以中间点划分左右子树，递归求得

2.2.4 Code109 有序链表转换为二叉搜索树

（1）构造辅助方法，进行递归，因为和数组不同的是，链表需要一个节点指示分组中点，需要两个参数

（2）递归停止条件，输入链表到达尾节点

（3）快慢指针法找到链表中点，作为数的根节点

（4）以中间点划分左右子树，递归求解，注意每个分组的尾节点

2.2.5 Code095 不同的二叉搜索树II

（1）构造辅助数组，指示子树的起始和终止位置

（2）递归结束条件, start > end，start == end new(node)

（3）遍历每个数组作为根节点

（4）生成左右子树的所有可能组合

（5）组合左右子树的可能情况

2.2.6 Code144 二叉树的前序遍历

（1）递归停止条件，节点为空

（2）添加节点到结果中

（3）递归左节点

（4）递归右节点

2.2.7 Code145 二叉树的后序遍历

（1）递归停止条件，节点为空

（2）递归左节点

（3）递归右节点

（4）添加节点到结果

2.2.8 Code094 二叉树的中序遍历

（1）递归停止条件，节点为空

（2）递归左节点

（3）添加节点到结果

（4）递归右节点

2.2.9 Code102 二叉树的层序遍历

    注意：由于结果需要每层保存在一个单独的链表中，故在遍历队列时，需要记录每层的元素个数。

（1）定义队列

（2）存放头节点，开启算法

（3）迭代条件，队列不为空

（4）创建链表保存该层节点

（5）遍历当前队列长度len个元素

（6）弹出头元素

（7）若左节点不为空，加入队列

（8）若右节点不为空，加入队列

（9）当前头元素存放结果

2.2.10 Code107 二叉树的层次遍历II

    与上一题不同的是，需要从底层向上遍历。只需要最后倒置链表即可。

（1）二叉树的层序遍历

（2）Collections.reverse(res)使用集合类翻转链表

2.2.11 Code103 二叉树的锯齿形层次遍历

（1）定义队列

（2）存放头节点，开启算法

（3）定义标识，区别两个遍历方向

（4）迭代条件，队列不为空

（5）创建链表保存该层节点

（6）遍历当前队列长度len个元素

（7）弹出头元素

（8）若左节点不为空，加入队列

（9）若右节点不为空，加入队列

（10）当前头元素存放结果

（11）遍历len个元素后，根据flag翻转当前链表

（12）取反flag标识

2.2.12 Code112 路径总和

（1）递归停止条件，左节点和右节点为空，即为叶节点

（2）递归左子树和右子树，输入参数每次减去当前节点的值。两个分支可以直接用或||相连

2.2.13 Code113 路径之和II

（1）构造辅助方法，参数为root，sum, list，进行递归

（2）递归停止条件，节点为空

（3）当前节点加入列表

（4）递归停止条件，到达叶节点，且sum == val

（5）满足停止条件，将链表加入结果集（这里注意不可以加return，因为需要回溯）

（6）递归左子树，输入参数每次减去当前节点值

（7）递归右子树，输入参数每次减去当前节点值

（8）左右子树执行完要去掉最后一个节点，为下一次迭代做准备

2.2.14 Code104 二叉树的最大深度

（1）递归停止条件，节点为空

（2）对左右子树进行递归，每次递归将左右子树的最大深度+1返回

2.2.15 Code111 二叉树的最小深度

（1）递归停止条件，到达叶节点

（2）递归，特殊情况1 只有左子树，无右子树，需要继续对左子树递归

（3）递归，特殊情况1 只有右子树，无左子树，需要继续对右子树递归

（4）递归，正常情况，左右子树最小深度+1递归

2.2.16 Code098 验证二叉搜索树

（1）中序遍历结果存储链表

（2）判断链表元素是否是升序排列

2.2.17 Code099 恢复二叉搜索树

（1）定义三个节点，用于保存错位的节点

（2）定义一个方法，找到顺序错误的两个节点

（3）递归停止条件，节点为空

（4）递归，左子树

（5）若prev节点不为空，且prev大于当前节点，赋值n1和n2节点

（6）将当前节点赋值prev

（7）递归，右子树

（8）找到错位节点后，交换两个节点的数值val

2.2.18 Code100 相同的树

（1）递归停止条件1 两个节点都为空，返回true

（2）递归停止条件2 一个节点为空，一个节点不为空，返回false

（3）递归左右子树，且节点值相等时，返回true

2.2.19 Code101 对称二叉树

（1）构造辅助方法递归，传入参数为左右节点

（2）递归停止条件1 左右子树都为空

（3）递归停止条件2 左右子树其中一个空一个不为空

（4）递归, 节点值相同，交换左右节点参数位置，递归结果仍相同，则返回true

2.2.20 Code110 平衡二叉树

（1）构造辅助方法，计算一个树或者子树的深度

（2）递归，当左右子树的深度差不大于1，且递归左右子树都成立，返回true

2.2.21 Code114 二叉树展开为链表

    思路：递归实现，暂存右结点，将左结点接在根结点右边，然后把暂存的右结点接在后面

可以看出来变化后每个节点其实都是指向了在先序遍历中的后一个节点。所以就通过栈的方式来先序遍历原树，如果一个节点有左节点，那么把它的右节点压栈（如果有的话），右指针指向原来的左节点；如果一个节点没有子节点，应该把它的右指针指向栈顶的节点

（1）定义一个point指针，方便算法中修改指针，初始化为头节点

（2）定义一个栈

（3）将头节点入栈，开启算法

（4）迭代条件，栈不为空

（5）弹出头节点

（6）当前节点右节点不为空，压栈

（7）当前节点左节点不为空，压栈

（8）当point指针不是当前节点时，point右指针指向当前节点，左指针指向Null

（9）当前节点赋值point节点，推动算法进行

2.2.22 Code129 求根到叶节点数字之和

（1）构造辅助方法，传入参数为根节点和当前和

（2）递归停止条件1，输入节点为空，这里必须返回0，代表没有到达叶节点，不能返回sum

（3）计算当前和 sum = sum * 10 + root.val

（4）递归停止条件2 ， 到达叶节点，返回当前和

（5）递归，左子树的和 + 右子树的和

2.2.23 Code124 二叉树的最大路径和

（1）定义全局遍历最大值变量，初始化为Integer.MIN_VALUE

（2）递归停止条件，节点为空

（3）递归，左子树

（4）递归，右子树

（5）若左右子树递归结果不大于0 ，赋值为0

（6）取当前最大值和l + r + root.val中的最大值

（7）方法返回值为左右子树的最大值+当前节点值

2.2.24 Code116 填充每个节点的下一个右侧节点指针

（1）递归停止条件，节点为空

（2）若有左节点。左节点指针指向右节点

（3）若有左节点，且当前节点的next指针不为空，右节点的next指针，指向当前节点next节点的左节点

（4）递归，左节点

（5）递归，右节点

2.2.25 Code117 填充每个节点的下一个右侧节点指针II

（1）递归停止条件 节点为空

（2）左右节点都不为空时

（3）左节点next指针指向右节点

（4）顺着root的next指针找，知道找到一个节点有左子树或者右子树，用root的右子树连上

（5）如果当前节点右子树为空，左子树不为空时

（6）顺着root的next指针找，知道找到一个节点有左子树或者右子树，用root的左子树连上

（7）如果当前节点左子树为空，右子树不为空时

（8）顺着root的next指针找，知道找到一个节点有左子树或者右子树，用root的右子树连上

（9）递归,必须先递归右子树

（10）递归左子树

2.3 链表

小结：

（1）很多时候需要修改或者变动表头节点，可以构造一个新的辅助表头节点指向头节点进行算法运算。

（2）链表大多使用迭代进行运算

2.3.1 Code002 两数相加

（1）构造辅助头节点

（2）定义一个对应位置的和变量，初始化为

（3）迭代条件：l1或者l2节点不为空，或者和变量大于0（有进位，这个条件不能忘）

（4）和变量赋值局部变量sum

（5）l1不为空，则sum值加上l1节点值，l1指向下一个节点

（6）l2不为空，则sum值加上l2节点值，l2指向下一个节点

（7）如果sum > 9进行进位,s =1 ,sum-= 10

（8）构造新节点赋值sum

（9）新节点加在辅助节点后面，辅助节点后移一位进行下一次迭代

（10）返回辅助头节点的下一个节点

2.3.2 Code019 删除链表的倒数第N个节点

思路：加一个虚假头结点dummy，并使用双指针p1和p2。p1先向前移动n个节点（从dummy节点开始移动，所以移动了n其实是移动到了前一位），然后p1和p2同时移动，当p1.next==None时，此时p2.next指的就是需要删除的节点前面一个节点，将其指向.next.next即可。

    相当于让p1指针永远比p2指针多走len-n个节点，则p1到表尾时，p2刚好到倒数第N个。

（1）构造辅助头节点

（2）辅助头节点的下一个节点指向头节点

（3）定义两个指针p1和p2，初始化指向辅助头节点

（4）p1先顺着链表前进n个节点

（5）迭代条件 p1是否到达表尾

（6）p1和p2一起向表尾移动

（7）此时p2为倒数第N个节点的前一个指针，调整next指针即可

（8）返回辅助节点的下一个节点

2.3.3 Code021 合并两个有序链表

    类似归并排序

（1）构造辅助头节点

（2）迭代条件：l1和l2不为空节点

（3）比较l1和l2当前节点的值，较小值添加到辅助头节点后面，且其指针后移一位

（4）l1和l2剩下的部分加入辅助节点后面

（5）返回辅助头节点的下一个节点

2.3.4 Code023 合并K个升序链表

    思路：最小堆方法。用一个大小为K的最小堆（用优先队列+自定义降序实现）(优先队列就是大顶堆，队头元素最大,自定义为降序后，就变成小顶堆，队头元素最小)，先把K个链表的头结点放入堆中，每次取堆顶元素，然后将堆顶元素所在链表的下一个结点加入堆中。

（1）定义最小堆

（2）将lists数组中的头节点全部放入优先级队列中

（3）构造辅助头节点

（4）迭代条件，队列不为空

（5）弹出对顶元素

（6）将弹出元素加入辅助节点后面

（7）若弹出元素下一个节点不为空则加入最小堆中

（8）返回辅助头节点的下一个节点

2.3.5 Code024 两两交换链表中的节点

（1）构造辅助头节点

（2）定义p1指针指向头节点

（3）辅助头节点Next指针指向头节点

（4）定义p2指针指向头节点的下一个节点

（5）迭代条件，p1和p2指针不为空

（6）保存p2的next节点为p3,进行节点交换

（7）移动辅助节点和p1节点的位置，为下一次遍历

（8）若p2节点不为空，则p2指向p3，为下一次遍历

（9）返回辅助节点的下一个节点

2.3.6 Code025 K个一组翻转链表

（1）构造辅助头节点，将一下个节点指向头节点

（2）迭代条件，输入节点不为空

（3）构建辅助方法，用于翻转k个链表，传入元素为当前k个元素的前一个节点

（4）检测是否有>=k个元素剩下

（5）不够k个节点直接返回

（6）当前k个节点的第一个节点

（7）为当前k个元素的前一个节点,为传入节点

（8）此时curr指向下一组k节点的头节点

（9）辅助方法，返回下一组k个节点的前一个节点，继续迭代

（10）返回辅助头节点的下一个节点

2.3.7 Code061 旋转链表

（1）构造辅助节点，下一个节点指向头节点

（2）统计链表长度，利用指针p

（3）计算哪个节点应该作为尾节点，step=链表长度-右移个数

（4）此时p指向链表最后一个节点，其next指针指向头节点

（5）循环移动节点

（6）此时P指向旋转后，应该作为结尾的节点

（7）尾节点的next指针作为头节点

（8）尾节点的next指针指向null

（9）返回找到的头节点

2.3.8 Code082 删除排序链表中的重复元素II

（1）构造辅助头节点，下一个节点指向头节点

（2）定义两个指针p和cur，分别指向辅助头节点和头节点

（3）迭代条件p.next不为空

（4）循环，若cur.next不为空，且两个指针的next节点值相等，cur节点后移

（5）若无重复节点即cur = p.next，两个指针都后移

（6）若有重复节点，P.next指针指向cur.next节点

（7）返回辅助头节点的下一个节点

2.3.9 Code083 删除排序链表中的重复元素

（1）定义一个set集合

（2）定义一个辅助头节点

（3）定义cur指针，指向辅助头节点

（4）迭代条件，链表没有遍历完

（5）如果set集合没有包含该节点值，则加入set中，cur的next指针指向该节点, cur指针后移

（6）head指针后移

（7）遍历结束后，cur指针指向null，作为链表结尾标志

（8）返回辅助头节点的下一个节点

2.3.10 Code086 分割链表

（1）定义辅助头节点，next指针指向头节点

（2）定义小于链表头节点

（3）定义大于等于链表头节点

（4）迭代条件，遍历节点不为空

（5）如果当前节点值小于输入值，加入小于链表，小于指针后移

（6）否则加入大于等于链表，大于等于指针后移

（7）小于链表尾指针指向大于等于链表头节点

（8）大于等于链表尾指针指向Null

（9）返回小于链表头节点

2.3.11 Code092 反转链表II

（1）构造辅助头节点，下一个节点指向头节点

（2）找到第m个节点

（3）保存m个节点的前一个节点，方便反转后接上

（4）迭代条件，遍历次数小n-m

（5）遍历结束后处理好m到n前后的节点

（6）返回辅助头节点的下一个节点

2.3.12 Code141 环形链表

（1）定义快慢指针

（2）迭代条件，fast指针和其next指针不为空

（3）快慢指针后移

（4）如果有一时快慢指针重合，则证明有环

（5）如果迭代中没有返回结果，则没有环，返回false

2.3.13 Code142 环形链表II

（1）定义快慢指针

（2）迭代条件，fast指针不为空，且其next指针也不为空

（3）快慢指针后移

（4）如果某一时刻，快慢指针重合，证明有环

（5）快指针回到头节点

（6）子迭代条件，快慢指针不重合

（7）快慢指针同幅度后移

（8）子迭代结束，返回快指针节点即为交点

（9）迭代结束时还没有返回，则没有环，返回null

2.3.14 Code143 重排链表

（1）定义快慢指针

（2）定义计数变量

（3）找到链表中点，并计数到中点的节点个数

（4）慢指针指向后半段第一个节点

（5）定义变量half保存链表一半长度

（6）迭代条件，慢指针不为空

（7）快指针指向头节点

（8）快指针后移half个长度

（9）变化后半段的头节点和前半段的尾节点关系

（10）对慢指针重新赋值，half变量减一，为下一次迭代做准备

（11）将中间节点的next指针指向Null，标志新链表结尾

2.3.15 Code147 对链表进行插入排序

（1）构造辅助头节点，下一个节点指向头节点

（2）定义指针变量p1保存头节点的next节点

（3）将头节点的next节点指向null

（4）迭代条件，p1不为空

（5）定义p2指针指向辅助头节点

（6）子迭代条件，p2的next指针不为空，且p2.next节点的值小于p1节点的值，则p2后移

（7）子迭代结束，将P1插入p2节点后

（8）赋值p1节点，为下一次迭代准备

（9）返回辅助头节点的下一个节点

2.3.16 Code148 排序链表

    链表形式的归并排序

（1）递归停止条件，头节点或者头节点的next节点为空

（2）定义快慢指针

（3）找到链表中点

（4）定义两个指针分别指向前后两端的头节点

（5）将中点节点的next指针指向null，分为两个链表

（6）递归前半段

（7）递归后半段

（8）定义辅助方法，进行归并排序，输入参数为前后两段链表的头节点

（9）如果一个链表为空直接返回另一个链表的表头节点

（10）构造辅助头节点

（11）迭代条件，两个头节点不为空

（12）哪个节点的值小，则加入辅助头节点后面，并且指针后移

（13）迭代结束，哪个节点不为空，直接加到辅助节点后面

（14）方法返回辅助头节点的下一个节点

（15）调用辅助方法排序

（16）返回归并后的新节点

2.4 DFS/回溯算法

（1）回溯法

    回溯法采用试错的思想，它尝试分步的去解决一个问题。在分步解决问题的过程中，当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候，它将取消上一步甚至是上几步的计算，再通过其它的可能的分步解答再次尝试寻找问题的答案。

回溯法通常用最简单的递归方法来实现，在反复重复上述的步骤后可能出现两种情况：

        · 找到一个可能存在的正确的答案

        · 在尝试了所有可能的分步方法后宣告该问题没有答案

    在最坏的情况下，回溯法会导致一次复杂度为指数时间的计算。

（2）有不重复要求的题目

    · 可以考虑先对数组进行排序，遇到重复元素，考虑continue关键字

    · 也可以考虑使用一个boolean数组，记录数组中的数是否被使用过

（3）可以先对题目给出的例题输出结果进行分析，看看是否有规律，或是发现递归的规律

2.4.1 Code017 电话号码的字母组合

（1）定义map集合，映射数字到字符串

（2）定义辅助方法dfs，输入参数为给定字符串、index变量记录下标、StringBuffer缓存结果

（3）递归停止条件，index下标到达给定字符串长度

（4）此时将buffer加入结果集

（5）取给定字符串中当前index下标对应的字符

（6）获取字符映射的字符串

（7）迭代条件，遍历映射字符串

（8）将当前映射字符串对应下标的字符加入buffer中

（9）递归，输入参数：给定字符串、index + 1、StringBuffer

（10）回溯，从buffer中删除当前映射字符串对应下标的字符

2.4.2 Code022 括号生成

    思路：如果左括号数量不大于 nn，我们可以放一个左括号。如果右括号数量小于左括号的数量，我们可以放一个右括号。

（1）定义辅助方法，输入参数为 StringBuffer缓存结果，左括号数量，右括号数量，左括号最大长度

（2）如果buff达到最大长度，将结果加入结果集

（3）若左括号没有到最大长度，buffer加入左括号

（4）递归左括号，输入参数，左括号数量加1

（5）回溯左括号，删除buffer最后一个字符

（6）若有括号数比左括号数小

（7）buffer加入右括号

（8）递归有括号，输入参数，右括号数量加1

（9）回溯右括号，删除buffer最后一个字符

2.4.3 Code039 组合总和

（1）定义辅助方法，输出参数为：数组，目标数，List缓存中间结果, 开始查找下标

（2）递归停止条件，target小于0

（3）递归停止条件，target递减为0

（4）将list结果加入结果集

（5）迭代，开始查找下标到数组结束的遍历

（6）若target减去当前下标对应的数组值，结果不为负

（7）将当前数加入list

（8）递归，输入参数，target值减去当前数， 开始查找下标为当前下标

（9）回溯，list链表删除最后一个元素

2.4.4 Code040 组合总和II

（1）排序数组，去掉重复的前提

（2）定义辅助方法，输入参数：数组，目标值，查找起始下标index，list缓存中间结果

（3）递归停止条件，target递减为0，将list结果加入结果集

（4）迭代，从起始下标遍历到数组结束

（5）如果target值减去当前数小于0，直接退出遍历

（6）若当前遍历第1个数后，碰到数组中数值相等直接continue

（7）将当前数加入List

（8）递归，输入参数为，target减去当前值，起始下标+1

（9）回溯，删除list最后一个数

2.4.5 Code046 全排列

（1）定义辅助方法，输入参数为：数组、list缓存中间结果

（2）递归停止条件，链表长度到达数组长度

（3）将List加入结果集

（4）遍历数组

（5）如果list中已经包含当前数，直接continue

（6）当前数加入链表

（7）递归，输入参数不变

（8）回溯，移除当前添加数

2.4.6 Code047 全排列II

（0）排序（升序或者降序都可以），排序是剪枝的前提

（1）构造辅助方法，输入参数为：数组、布尔数组、list缓存结果

（2）递归停止条件，list长度到达数组长度

（3）将list加入结果集

（4）迭代，遍历数组

（5） 如果当前数已经被使用，直接continue

（6）从第1个节点后，遇到相等的数，且相等的数已经被使用，直接continue

（7）当前数加入List中

（8）布尔数组中相应下标置为true

（9）递归，输入参数不变

（10）回溯，布尔数组中当前下标置位false

（11）回溯，删除list最后一个元素

2.4.7 Code051 N皇后

（1）定义n*n的char数组保存棋盘

（2）棋盘初始化为全 ‘.’

（3）构造辅助方法，输入参数为：char数组，变量row表示当前行

（4）递归停止条件，当前行到达数组最大行数

（5）构造将char数组，变为String输出的方法

（6）将数组转为字符串后加入结果集

（7）迭代，遍历每一列

（8）构造辅助方法，判断当前位置是否可以填充Q字符

（9）判断当前列有无皇后

（10）判断右上角有无皇后

（11）判断左上角有无皇后

（12）若可以填充Q字符

（13）当前位置变为‘Q’

（14）递归，输入参数，row + 1

（15）回溯，将当前位置置为'.'

2.4.8 Code052 N皇后II

（1）定义全局变量count，用于对结果计数

（2）定义n*n的char数组保存棋盘

（3）棋盘初始化为全 ‘.’

（4） 构造辅助方法，输入参数为：char数组，变量row表示当前行

（5）递归停止条件，当前行到达数组最大行数

（6）count加1

（7）迭代，遍历每一列

（8）构造辅助方法，判断当前位置是否可以填充Q字符

（9）判断当前列有无皇后

（10）判断右上角有无皇后

（11）判断左上角有无皇后

（12）若可以填充Q字符

（13）当前位置变为‘Q’

（14）递归，输入参数，row + 1

（15）回溯，将当前位置置为'.'

2.4.9 Code060 排列序列

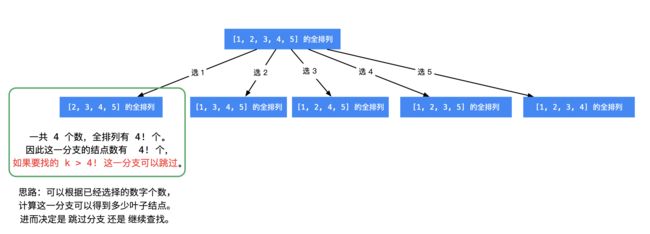
    思路：所求排列 一定在叶子结点处得到，进入每一个分支，可以根据已经选定的数的个数，进而计算还未选定的数的个数，然后计算阶乘，就知道这一个分支的 叶子结点 的个数：

    · 如果 k 大于这一个分支将要产生的叶子结点数，直接跳过这个分支，这个操作叫「剪枝」；

    · 如果 kk小于等于这一个分支将要产生的叶子结点数，那说明所求的全排列一定在这一个分支将要产生的叶子结点里，需要递归求解。

图2-1 LeetCode060

（1）定义一个阶乘数组，长度为n + 1，并将计算结果存在数组中

（2）定义布尔数组，标识下标数是否使用过，长度为n + 1，初始化为false

（3）定义辅助方法，输入参数为：元素变量index，strbuff缓存结果

（4）递归停止条件，index递增至n

（5）计算还未确定的数字的全排列的个数

（6）迭代，遍历1-n个数

（7）如果当前数被使用过，直接continue

（8）未确定数字的全排列个数小于k, k减去当前计数后，直接continue

（9）将当前数加入strbuff中

（10）将布尔数组对应位置置为true

（11）递归，输入参数，index + 1

2.4.10 Code077 组合

（1）构造辅助方法，输入参数为，n，k，起始元素index，list缓存结果

（2）若list长度到达k

（3）将list加入结果集

（4）遍历，从起始元素index到n

（5）将当前元素加入list

（6）递归，输入元素，起始元素 + 1

（7）回溯，去掉List的最后一个元素

2.4.11 Code078 子集

（1）构造辅助方法，输入参数为：数组，起始下标，list缓存结果

（2）迭代，从起始下标开始遍历到数组结束

（3）当前数加入list

（4）list加入结果集

（5）递归，输入参数为，起始下标 +  1

（6）回溯，删除list最后一个元素

2.4.12 Code079 单词搜索

（1）构造代表上下左右四个位置的二维数组

（2）定义布尔数组，代表是否使用了当前字符

（3） 双层循环遍历数组

（4）构造辅助方法，输入参数：当前行数，当前列数，字符串当前下标

（5）递归停止条件，当字符串下标到达最后一个下标，只需要判断，当前字符是否等于字符串最后一个字符

（6）若当前位置和字符串下标位置字符相等

（7）布尔数组相应位置置为true

（8）遍历，当前位置的上下左右4个位置

（9）获取周边点的位置

（10）若点在数组范围内，且没有被使用

（11）递归，输出参数，周边点的位置，字符串下标 + 1

（12）若递归返回值为true，直接返回true

（13）回溯，遍历4个位置结束后，将当前位置的布尔数组置为false

（14）若遍历中没有返回true，则方法返回false

2.4.13 Code090 子集II

（1）对数组排序

（2）将空集加入结果集

（3）构造辅助方法，输入参数为：数组，起始下标，list缓存结果

（4）迭代，从起始下标到数组结束

（5）剩余数组中遇到重复的跳过

（6）将当前数加入List

（7）将当期list加入结果集

（8）递归，输入参数为，起始下标 + 1

（9）回溯，去掉list的最后一个元素

2.4.14 Code093 复原IP地址

（1）若字符串长度大于12或小于4，直接返回

（2）构造辅助方法，输入参数为：字符串下标，地址段，list缓存中间结果

（3）递归停止条件，如果字符串下标到达末尾，地址段递减为0，将当前结果加入结果集

（4）遍历，一个节点最多只能是三位数

（5）若字符串下标超出维度，直接break

（6）如果地址段*3后长度小于剩余字符串长度，直接continue

（7）构造方法判断地址是否有效

（8）判断从begin到i位置的地址是否有效

（9）有效则将该段地址加list

（10）递归，输入参数，起始位置+1，地址段-1

（11）回溯，删掉表尾元素

2.4.15 Code131 分割回文串

（1）构造辅助方法，输入参数：字符串，字符串下标变量，list缓存结果

（2）递归停止条件，下标到达字符串尾部

（3）将list加入结果集

（4）遍历，从下标变量开始到字符串结尾

（5）编写方法检测指定段是否为回文串

（6）如果不是回文串，直接continue

（7）当前子串加入list

（8）递归，输入参数，下标+1

（9）回溯，去掉list最后一个元素

2.4.16 Code037 解数独

思路：

    · 数独首先行，列，还有 3*3 的方格内数字是 1~9 不能重复。

    · 声明布尔数组，表明行列中某个数字是否被使用了， 被用过视为 true，没用过为 false。

    · 初始化布尔数组，表明哪些数字已经被使用过了。

    · 尝试去填充数组，只要行，列， 还有 3*3 的方格内 出现已经被使用过的数字，我们就不填充，否则尝试填充。

    · 如果填充失败，那么我们需要回溯。将原来尝试填充的地方改回来。

    · 递归直到数独被填充完成。

（1）定义三个布尔数组 表明 行, 列, 还有 3*3 的方格的数字是否被使用过

（2）初始化，数组中的现有数进行判断，填充三个boolean数组

（3）构造辅助方法，输入参数：棋盘数组、三个boolean数组，行变量，列变量

（4）递归停止条件，如果列变量到达边界，列变量置为0，行变量+1，如果行变量也到达边界， 返回true, 表示一切结束

（5）判断当前位置是否是空，是空则尝试填充, 否则递归，列变量+1

（6）遍历9个数字，尝试填充1-9

（7）定义变量，判断当前数是否被填充过

（8）如果没有填充，将三个Boolean数组相应位置变为true

（9）将当前数填入棋盘

（10）递归，列变量+1，如果下一个结果也为true，直接返回true

（11）回溯，棋盘和三个数组变为原来的状态

（12）如果前述所有结果没有返回，最后返回false

（13）调用辅助方法，初始位置为0,0

2.4.17 Code126 单词接龙II

2.4.18 Code130 被围绕的区域

思路：任何边界上的 O 都不会被填充为 X。 我们可以想到，所有的不被包围的 O 都直接或间接与边界上的 O 相连。我们可以利用这个性质判断 O 是否在边界上，具体地说：

· 对于每一个边界上的 O，我们以它为起点，标记所有与它直接或间接相连的字母 O；

· 最后我们遍历这个矩阵，对于每一个字母：

    · 如果该字母被标记过，则该字母为没有被字母 X 包围的字母 O，我们将其还原为字母 O；

    · 如果该字母没有被标记过，则该字母为被字母 X 包围的字母 O，我们将其修改为字母 X。

（1）遍历左右边界，调用辅助方法

（2）遍历上下边界，调用给你辅助方法

（3）再次遍历整个数组

（4）若元素被标记为A,则变为O

（5）如果元素是O，则边为X

（6）定义dfs辅助方法，传入位置参数

（7）递归停止条件，位置参数越界或者当前元素不是O

（8）标记当前元素为A

（9）递归下上左右四个位置

2.4.19 Code133 克隆图

（1）定义哈希表

（2）递归停止条件 节点为空

（3）若当前节点在哈希表内，直接返回当前哈希表的value

（4）新建节点

（5）当前节点为key，新建节点为value，放入哈希表

（6）遍历当前节点的邻接链表

（7）递归当前邻接节点，递归返回的节点加入新建节点的邻接链表

2.5 哈希表

2.5.1 Code001 两数之和

思路： 利用哈希表保存 target-当前数 作为key，当前数下标为value

（1）定义哈希表

（2）遍历数组

（3）如果存在 target - nums[i] 的key,找到了，返回两个下标

（4）不存在，则num[i]为key，下标为value

（5）遍历结束后没有找到，返回0,0

2.5.2 Code036 有效的数独

（1）定义一个set集合

（2）判断条件1是否满足

（3）当 当前数不为'.'时，加入set，若重复直接返回false

（4）一个子循环结束，清空set集合

（5）同理，判断条件2是否满足，判断条件3是否满足

2.5.3 Code049 字母异位词分组

（1）定义一个HashMap

（2）遍历字符串数组

（3）将当前字符串转为字符数组，并排序

（4）若key不在map中，则新建链表

（5）加入对应key的链表中

2.5.4 Code128 最长连续序列

（1）定义Set集合，将数组中所有元素加入

（2）定义结果变量

（3）遍历set集合

（4）当前数的前一个数不在集合中，进行运算

（5）自迭代，判断以当前数开始的最大连续数是多少，并更新结果变量

2.5.5 Code146 LRU缓存机制

思路：

    用一个哈希表和一个双向链表维护所有在缓存中的键值对。

· 双向链表按照被使用的顺序存储了这些键值对，靠近头部的键值对是最近使用的，而靠近尾部的键值对是最久未使用的。

· 哈希表即为普通的哈希映射（HashMap），通过缓存数据的键映射到其在双向链表中的位置。

    这样以来，我们首先使用哈希表进行定位，找出缓存项在双向链表中的位置，随后将其移动到双向链表的头部，即可在 O(1) 的时间内完成 get 或者 put 操作。具体的方法如下：

· 对于 get 操作，首先判断 key 是否存在：

    · 如果 key 不存在，则返回 -1−1；

    · 如果 key 存在，则 key 对应的节点是最近被使用的节点。通过哈希表定位到该节点在双向链表中的位置，并将其移动到双向链表的头部，最后返回该节点的值。

· 对于 put 操作，首先判断 key 是否存在：

    · 如果 key 不存在，使用 key 和 value 创建一个新的节点，在双向链表的头部添加该节点，并将 key 和该节点添加进哈希表中。然后判断双向链表的节点数是否超出容量，如果超出容量，则删除双向链表的尾部节点，并删除哈希表中对应的项；

    · 如果 key 存在，则与 get 操作类似，先通过哈希表定位，再将对应的节点的值更新为 value，并将该节点移到双向链表的头部。

2.6 双指针/滑动窗口

2.6.1 Code003 无重复字符的最长子串

思路：假设我们选择字符串中的第 k 个字符作为起始位置，并且得到了不包含重复字符的最长子串的结束位置为 rk。那么当我们选择第k+1 个字符作为起始位置时，首先从k+1 到rk的字符显然是不重复的，并且由于少了原本的第 k 个字符，我们可以尝试继续增大 rk直到右侧出现了重复字符为止。

（1）定义哈希集合，记录每个字符是否出现过

（2）定义右指针和结果计数变量

（3）迭代，字符串长度

（4）若当前下标（左指针）不为0，删除set集合中的一个字符

（5）循环，停止条件为右指针越界或者set集合中已经包含当前元素

（6）不断地移动右指针，当前字符加入集合，

（7）选出结果计数变量和此次循环长度的最大值，并更新计数变量

2.6.2 Code009 回文数

思路：先将数字按位分割到一个整数数组中，利用首尾两个指针迭代判断是否相等。

2.6.3 Code015 三数之和

思路：将num[i]的相反数即-num[i]作为target，然后从i+1到len(num)-1的数组元素中寻找两个数使它们的和为-num[i]就可以了。

（1）排序数组

（2）定义下标变量，进行迭代

（3）迭代条件：index < nums.length - 2

（4）若当前数大于0直接break

（5）定义左右指针，分别指向index+1和nums最后一个数

（6）子迭代，迭代条件左指针小于右指针

（7）定义sum为index值，左右指针值的三数之和

（8）如果sum ==0 ，加入结果集，并对左右指针前后的值进行去重

（9）如果sum < 0，左指针右移

（10）如果sum > 0，右指针左移

（11）对index后面的值进行去重

2.6.4 Code016 最接近的三数之和

（1）定义下标变量

（2）排序数组

（3）定义close结果变量，代表与target的距离，可以为负数，初始化为Integer最大值

（4）迭代，迭代停止条件，index < nums.length - 2

（5）去重,设定循环条件，index == 0或者当前数大于前一个数

（6）定义左右两个指针，初始化为index + 1和数组最后一个下标

（7）子迭代条件,左指针小于右指针

（8）定义变量，sum 为index下标，左右指针下标的三数之和，减去target

（9）比较并更新close值

（10）若sum==0，直接return；若sum<0，左指针右移；若sum > 0，右指针左移

（11）下标+1

（12）close+target返回

2.6.5 Code018 四数之和

（1）排序数组

（2）for循环，下标小于nums.length-3

（3）去重,设定循环条件，i == 0或者当前数大于前一个数

（4）子迭代，下标从i+1到nums.length-2

（5）去重，设置循环条件，j==i + 1或者当前数大于前一个数

（6）定义左右指针，初始化为j+1和数组最后一个下标

（7）子迭代，左指针小于右指针

（8）定义sum为前面四个下标对应的四数之和

（9）如果sum==target，加入结果集，对左右指针去重

（10）如果sum < target，左指针右移

（11）如果 sum>target，右指针左移

2.6.6 Code026 删除排序数组中的重复项

（1）定义结果计数变量

（2）迭代，遍历整个数组长度

（3）从第二个元素，若遇到相同元素，直接continue

（4）如果下标和结果计数变量不同，则将当前下标数复制到结果变量处

（6）结果变量+1

2.6.7 Code027 移除元素

（1）定义结果指针

（2）遍历数组

（3）当当前数不等于val时，当前数复制给结果指针，结果指针+1

2.6.8 Code030串联所有单词的子串

2.6.9 Code069 x的平方根

思路： 二分法，一个数的平方根最多不会超过它的一半。

（1）定义左右指针，初始化为0和中间值

（2）迭代，左指针不大于右指针

（3）若之间值的乘积大于x，则右指针移动,否则左指针移动

（4）因为一定存在，因此无需后处理,直接返回左指针

2.6.10 Code074 搜索二维矩阵

思路：m x n 矩阵可以视为长度为 m x n的有序数组。该 虚 数组的序号可以由下式方便地转化为原矩阵中的行和列 (我们当然不会真的创建一个新数组) ，该有序数组非常适合二分查找。

row = idx / n ， col = idx % n

（1）定义左右指针，初始化为0和数组最后一个数

（2）迭代，迭代条件左指针小于等于右指针

（3）得到中间点虚数组下标

（4）得到该下标在原数组中的大小

（5）比较结果并移动指针

2.6.11 Code076最小覆盖子串

思路：一个用于「延伸」现有窗口的 r 指针，和一个用于「收缩」窗口的 l 指针。在任意时刻，只有一个指针运动，而另一个保持静止。我们在 s 上滑动窗口，通过移动 r 指针不断扩张窗口。当窗口包含 t 全部所需的字符后，如果能收缩，我们就收缩窗口直到得到最小窗口。

（1）定义两个哈希表

（2）遍历t字符串，字符作为key，出现次数作为value

（3）定义左右指针，分别初始化为-1和0

（4）定义结果的左右指针

（5）迭代条件，右指针不越界s字符串长度

（6）右指针+1

（7）若右指针没越界，且当前字符在t的哈希表中

（8）将当前字符和计数值，加入另一个哈希表中

（9）定义辅助方法，根据计数值判断是否当前区间可能满足t

（10）定义迭代器，遍历t的哈希表

（11）若s的哈希表当前字符计数值小于t的计数值，直接返回false

（12）若前面都没返回，则返回true

（13）子迭代，子迭代条件，辅助方法返回true，且左指针小于等于右指针

（14）若 当前窗口长度比之前更小，更新结果长度变量

（15）若t的哈希表包含当前窗口左指针的key，s的哈希表对应value-1

（16）左指针右移，继续子迭代

2.6.12 Code080 删除排序数组中的重复项II

（1）定义左右指针，初始化为1和nums.length

（2）定义一个计数值，初始化为1

（3）迭代，迭代条件左指针小于右指针

（4）若当前值等于前一个值，计数值+1   

（5）定义辅助方法，将但当前下标开始的所有数往前移动一位

（6）若计数值大于2,调用辅助方法移动左指针下标后的值

（7）左右指针左移一位

（8）若当前值不等于前一个值，计数值置为1

（9）返回右指针即为现有数组长度

2.6.13 Code125 验证回文串

（1）定义StrinBuff，遍历字符串将字母和数字转成小写加入

（2） 定义左右指针，初始化为一头一尾

（3）迭代，迭代条件为左指针小于右指针

（4）当左右指针对应值不等时，直接返回false

（5）迭代结束，返回true

2.7 纯思路

（1）在遇到倒置访问、对称之类的，可以考虑Stack栈的结构特性

（2）碰到排序（有序）数组时，优先考虑二分法及其变种。掌握搜索第一个大于等于一个数的方法。

        while (left <= right) {

            int mid = ((right - left) >> 1) + left;

            if (target <= nums[mid]) {

                ans = mid;

                right = mid - 1;

            } else {

                left = mid + 1;

            }

        }

2.7.1 Code004 寻找两个正序数组的中位数

2.7.2 Code006 Z字形变换

思路：根据numRows定义相应个数的StringBuffer，在后续算法中进行添加元素。定义flag为-1,并设置计数到numRows时改变flag为+1。

    public String convert(String s, int numRows) {

        if(numRows < 2) return s;

        List rows = new ArrayList();

        for(int i = 0; i < numRows; i++) rows.add(new StringBuilder());

        int i = 0, flag = -1;

        for(char c : s.toCharArray()) {

            rows.get(i).append(c);

            if(i == 0 || i == numRows -1) flag = - flag;

            i += flag;

        }

        StringBuilder res = new StringBuilder();

        for(StringBuilder row : rows) res.append(row);

        return res.toString();

    }

2.7.3 Code007 整数反转

思路：

（1）通过循环将数字x的每一位拆开，在计算新值时每一步都判断是否溢出。

（2）溢出条件有两个，一个是大于整数最大值MAX_VALUE，另一个是小于整数最小值MIN_VALUE，设当前计算结果为ans，下一位为pop。

（3）从ans * 10 + pop > MAX_VALUE这个溢出条件来看

    · 当出现 ans > MAX_VALUE / 10 且 还有pop需要添加 时，则一定溢出

    · 当出现 ans == MAX_VALUE / 10 且 pop > 7 时，则一定溢出，7是2^31 - 1的个位数

（4）从ans * 10 + pop < MIN_VALUE这个溢出条件来看

    · 当出现 ans < MIN_VALUE / 10 且 还有pop需要添加 时，则一定溢出

    · 当出现 ans == MIN_VALUE / 10 且 pop < -8 时，则一定溢出，8是-2^31的个位数

public int reverse(int x) {

        int ans = 0;

        while (x != 0) {

            int pop = x % 10;

            if (ans > Integer.MAX_VALUE / 10 || (ans == Integer.MAX_VALUE / 10 && pop > 7))

                return 0;

            if (ans < Integer.MIN_VALUE / 10 || (ans == Integer.MIN_VALUE / 10 && pop < -8))

                return 0;

            ans = ans * 10 + pop;

            x /= 10;

        }

        return ans;

    }

2.7.4 Code008 字符串转换整数

（1）字符串转为字符数组

（2）定义下标变量

（3）去掉前导空格

（4）去掉前导空格以后到了末尾了，直接返回0

（5）定义boolean变量标识符号

（6）遇到负号，符号标识为true，下标+ 1；

（7）否则，如果是“+”，下标+1；

（8）否则，如果字符不是数字，直接返回0

（9）迭代，条件为下标不越界，且当前字符为数字

（10）判断是否越界Integer范围

if (ans > (Integer.MAX_VALUE - digit) / 10) {

    // 本来应该是 ans * 10 + digit > Integer.MAX_VALUE

    // 但是 *10 和 + digit 都有可能越界，所有都移动到右边去就可以了。

    return negative? Integer.MIN_VALUE : Integer.MAX_VALUE;

}

（11）计算并更新结果，下标+1

（12）迭代结束后，根据符号标识返回结果

2.7.5 Code013 罗马数字转整数

（1）定义一个变量记录当前字符的前一个字符，初始化为第一个字符

（2）迭代，从1开始遍历字符串下标

（3）定义一个辅助方法，利用switch返回罗马字符对应的整数值；拿到当前字符对应的整数

（4）如果当前数大于前一个字符数，sum-preNum;否则相加

（5）更新pre变量为当前数，为后一次遍历准备

（6）sum加上第一个字符的数值

2.7.6 Code014 最长公共前缀

（1）定义下标变量

（2）定义StringBuffer变量

（3）迭代， 下标不越界数组第一个字符串的长度

（4）遍历数组中所有字符串

（5）若下标越界，或某个字符串当前下标字符不与第一个字符串当前下标字符相等，直接返回当前strbuff

（6）遍历结束不返回，将第一个字符串的当前下标值放入strbuf中，下标+1

2.7.7 Code020 有效的括号

（1）定义一个栈

（2）迭代整个字符串长度

（3）如果当前字符为左部分，加入栈

（4）如果当前字符为右部分，继续判断

（5）如果栈为空，直接返回false

（6）弹出栈顶元素，若不对称直接返回false

（7）迭代结束，若栈不为空，返回false

（8）前述都没有返回，则返回true

2.7.8 Code028 实现strStr()

思路：调用s.substring()方法遍历判断即可

2.7.9 Code029 两数相除

思路：可以简单概括为： 60/8 = (60-32)/8 + 4 = (60-32-16)/8 + 2 + 4 = 1 + 2 + 4 = 7

（1）如果被除数为Integer最小值，且除数为-1，返回Interger最大值

（2）异或，判断结果是不是负数

（3）考虑可能溢出问题，将除数和被除数都转为负数

（4）定义辅助方法计算结果

（5）递归停止条件，在被除数大于除数，返回0

（6）定义临时变量保存除数

（7）定义计数变量

（8）循环条件tmp + tmp < 0防止溢出且被除数小于2倍的临时变量

（9）计数变量和临时变量都翻倍

（10）递归，输入参数：被除数减去当前临时变量，除数不变 

（11）根据正负号判断结果

2.7.10 Code031 下一个排列

（1）找到从后往前第一个降序的数

（2）找到从后往前第一个比上面数大的数

（3）交换两个数

（4）定义辅助方法，从上述第一个数到数组末尾，两两交换中间的数

2.7.11 Code033 搜索旋转排序数组

思路：二分法的运用，详见JZ06

2.7.12 Code034 在排序数组中查找元素的第一个和最后一个位置

思路：二分查找中，寻找 leftIdx 即为在数组中寻找第一个大于等于target 的下标，寻找 rightIdx 即为在数组中寻找第一个大于 target 的下标，然后将下标减一。

（1）定义辅助方法找到左右下标，输入参数：数组、target、boolean值区分左右

（2）定义左右指针，初始化为数组两端

（3）迭代条件，左指针小于等于右指针

（4）定义中点变量

（5）判断中点大于和等于情况，右指针变化，结果变量复制中点变量

（6）小于情况，左指针变化

（7）得到左右指针后，判断符不符合条件

（8）不符合情况，返回两个-1

2.7.13 Code035 搜索插入位置

思路：将题目转化为“在一个有序数组中找第一个大于等于target 的下标”。参考34题即可

2.7.14 Code038 外观数列

（1）对小于2的情况，单独判断

（2）定义一个StringBuffer变量

（3）遍历0到n-2次

（4）定义计数变量，初始化为1

（5）子迭代，从1到字符串末尾

（6）如果当前字符和前一个字符不等，strbuff中加入计数变量和当前字符，计数变量初始化为1

（7）否则，计数变量+1

（8）子迭代结束后，strbuff中加入计数变量和最后一个字符

（9）更新结果字符串的值

（10）strbuff清空

2.7.15 Code041 缺失的第一个正数

（1）排序数组

（2）遍历数组

（3）若判断负数到正数的位置是否有1

（4）当当前数大于0时，判断伺候，是否不连续，否则返回缺少的数

（5）前面都没有返回，则最后返回数组末尾数+1

2.7.16 Code042 接雨水

思路：我们在遍历数组时维护一个栈。如果当前的条形块小于或等于栈顶的条形块，我们将条形块的索引入栈，意思是当前的条形块被栈中的前一个条形块界定。如果我们发现一个条形块长于栈顶，我们可以确定栈顶的条形块被当前条形块和栈的前一个条形块界定，因此我们可以弹出栈顶元素并且累加答案到ans 。

（1）定义一个栈

（2）如果栈顶元素一直相等，那么全都pop出去，只留第一个

（3）stackTop此时指向的是此次接住的雨水的左边界的位置。右边界是当前的柱体，即i。Math.min(height[stackTop], height[i]) 是左右柱子高度的min，减去height[curIdx]就是雨水的高度。 i - stackTop - 1 是雨水的宽度。

2.7.17 Code043 字符串相乘

思路：乘数 num1 位数为 M，被乘数 num2 位数为 N， num1 x num2 结果 res 最大总位数为 M+N

（1）定义一个m+n长的数组

（2）从后往前遍历两个字符串

（3）两两相乘从后往前放入新数组

（4）从后往前遍历新数组

（5）若当前数大于10，进行进位拆分

（6）讲数组用StringBuffer转为字符串

2.7.18 Code048 旋转图像

思路：将给定的矩阵分成四个矩形并且将原问题划归为旋转这些矩形的问题

2.7.19 Code50 Pow（x, n）

思路： 

    ·当我们要计算 x^n 时，我们可以先递归地计算出 y = x^⌊n/2⌋，其中⌊a⌋ 表示对 a 进行下取整；

    · 根据递归计算的结果，如果 n 为偶数，那么 x^n = y^2；如果 nn 为奇数，那么 x^n = y^2 * x

    · 递归的边界为 n = 0，任意数的 0 次方均为 1。

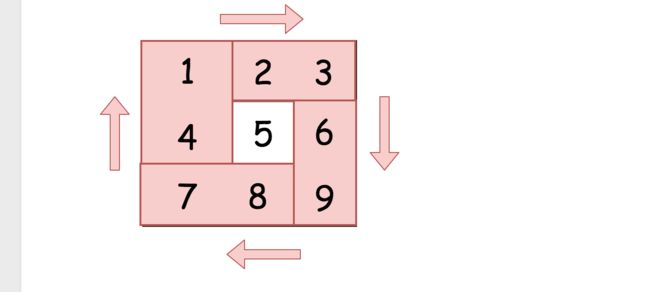
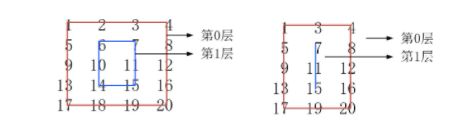
2.7.20 Code54 螺旋矩阵

思路：从外到内，按层打印

（1）定义一层的左上和右下顶点，确定矩形

（2）迭代，迭代条件：左上和右下顶点相对位置不变

（3）若在一条横线上，直接打印

（4）若在一条竖线上，直接打印

（5）正常情况，定义临时变量(r,c)

（6）按照顺时针方向遍历

2.7.21 Code056 合并区间

思路：首先，我们将列表中的区间按照左端点升序排序。然后我们将第一个区间加入 merged 数组中，并按顺序依次考虑之后的每个区间：

· 如果当前区间的左端点在数组 merged 中最后一个区间的右端点之后，那么它们不会重合，我们可以直接将这个区间加入数组 merged 的末尾；

· 否则，它们重合，我们需要用当前区间的右端点更新数组 merged 中最后一个区间的右端点，将其置为二者的较大值。

（1）利用Comparator设计二维数组的左端点排序

（2）定义结果链表

（3）遍历数组

（4）如果结果链表最后一个点的右区间小于当前点左区间，将当前点加入结果集

（5）否则，比较链表最后一个点的右区间和当前点的右区间，更新最后一个点的右区间

2.7.22 Code057 插入区间

思路：

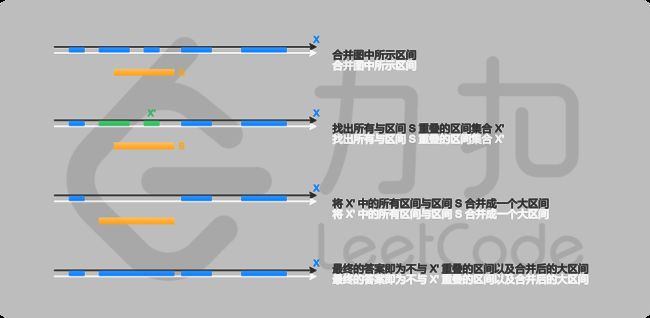
在给定的区间集合X 互不重叠的前提下，当我们需要插入一个新的区间 S =[left,right] 时，我们只需要：

· 找出所有与区间 S 重叠的区间集合X‘；

· 将X′中的所有区间连带上区间 S 合并成一个大区间；

· 最终的答案即为不与X′重叠的区间以及合并后的大区间。

（1）遍历二维数组

（2）第一次当前端点左区间大于给定区间右区间时，将给定区间加入结果集

2.7.23 Code058 最后一个单词的长度

（1）定义一个计数变量

（2）遍历整个字符串

（3）若当前字符不为空格，计数+1

（4）若当前字符为空格，下一个字符不为空格,计数变量置为0

2.7.24 Code59 螺旋矩阵II

思路：按层遍历

（1）定义一层的左上和右下点

（2）定义计数变量

（3）迭代，迭代条件：左上和右下点保持相对顺序

（4）当左上和右下点在同一行时，赋值n*n

2.7.25 Code065 有效数字

思路：先设定numSeen，dotSeen和eSeen三种boolean变量，分别代表是否出现数字、点和E

然后遍历目标字符串

· 判断是否属于数字的0~9区间

· 遇到点的时候，判断前面是否有点或者E，都需要return false

· 遇到E的时候，判断前面数字是否合理，是否有E，并把numSeen置为false，防止E后无数字

· 遇到-+的时候，判断是否是第一个，如果不是第一个判断是否在E后面，都不满足则return false

·其他情况都为false

· 最后返回numSeen的结果即可

（1）定义三个布尔值，标识数字、点和e

（2）将字符串去掉首尾空格后，转为字符数组

（3）遍历

（4）如果当前字符是数字，数字布尔量为true

（5）若果当前是'.'，并且点或者e的布尔量为true，直接返回false

（6）否则，将点布尔量为true

（7）如果当前是e，并且点布尔量为true或则数字布尔量为false,直接返回false

（8）否则，将点和数字布尔量置为true

（9）如果当前为+-号,若前一位不为e，则直接返回false

（10）其他情况都返回false

（11）遍历结束若没有返回，则返回数字布尔量

2.7.26 Code066 加一

（1）定义进位变量，初始化为1

（2）从后往前遍历数组

（3）当前数加上进位数

（4）和10的商作为心的进位值

（5）mod 10作为当前下标值

（6）遍历结束，若进位值为1

（7）新定义数组，长度+1

（8）将第一位置为1，其余为不需要赋值，肯定是0

（9）赋值结束后，返回新数组

（10）否则返回原数组

2.7.27 Code071 简化路径

（1）定义一个栈

（2）将路径以‘/’分割为一个字符串数组

（3）遍历该字符串数组

（4）若当前字符串不为空,进一步判断

（5）若当前字符串不为'.'和'..'，当前字符串入栈

（6）如果当前字符串为‘..’，若栈不为空，直接弹栈

（7）遍历结束后，若栈为空，返回'/'

（8）若不为空，弹栈并组合为字符串输出

2.7.28 Code073 矩阵置零

（1）定义一个二维布尔数组，用于标记是否已经访问过

（2）遍历二维数组

（3）若当前元素为0，且布尔值为false

（4）将当前位置布尔值置为true

（5）将当前行不为0的值，置为0，且布尔值置为true

（6）将当前列不为0的值，置为0，且布尔值置为true

2.7.29 Code075 颜色分类

思路：类似快排的方法

2.7.30 Code084 柱状图中最大的矩形

思路：单调栈

· 栈中存放了 j 值。从栈底到栈顶，j 的值严格单调递增，同时对应的高度值也严格单调递增；

· 当我们枚举到第 i 根柱子时，我们从栈顶不断地移除height[j]≥height[i] 的 j 值。在移除完毕后，栈顶的 j 值就一定满足height[j]

        · 这里会有一种特殊情况。如果我们移除了栈中所有的 j 值，那就说明 i 左侧所有柱子的高度都大于height[i]，那么我们可以认为 i 左侧且最近的小于其高度的柱子在位置j=−1，它是一根「虚拟」的、高度无限低的柱子。这样的定义不会对我们的答案产生任何的影响，我们也称这根「虚拟」的柱子为「哨兵」。

· 我们再将 i 放入栈顶。

（1）定义左右两个数组，用于两个方向的遍历

（2）定义栈，存储下标

（3）从左往右遍历数组

（4）子迭代，当栈不为空，且当前栈顶元素大于当前数时，弹栈

（5）子迭代结束，若当前栈为空，则left数组当前下标赋值-1，否则赋值栈顶下标

（6）当前下标入栈

（7）清除栈

（8）从右往左遍历数组

（9）子迭代，当栈不为空，且当前栈顶元素大于当前数时，弹栈

（10）子迭代结束，若当前栈为空，则right数组当前下标赋值len，否则赋值栈顶下标

（11）当前下标入栈

（12）遍历，在每个下标下计算当前最大面积，比较并更新结果

2.7.31 Code088 合并两个有序数组

思路：归并排序

2.7.32 Code089 格雷编码

思路：以二进制为 0 值的格雷码为第零项，第一项改变最右边的位元，第二项改变右起第一个为1的位元的左边位元，第三、四项方法同第一、二项，如此反复，即可排列出n个位元的格雷码。

（1）初始化第零项

（2）遍历，2^n

（3）得到上一个的值

（4）若同第一项的情况，和 0000001 做异或，使得最右边一位取反，结果加入结果集

（5）若同第二项的情况，寻找右边起第一个为 1 的位元，和 00001000000 类似这样的数做异或，使得相应位取反，结果加入结果集

2.7.33 Code118 杨辉三角

（1）初始化第一行

（2）迭代指定次数

（3）将上一行的第一个元素加入新链表头

（4）遍历，按照定义两两相加求解

（5）将上一行的最后一个元素加入新链表表尾

（6）将链表加入结果集

2.7.34 Code119 杨辉三角II

（1）定义一个链表tmp

（2）初始化第一行

（3）迭代指定次数

（4）定义当前行的列表

（5）将tmp链表第一个元素加入新链表头

（6）遍历，按照定义两两相加求解

（7）将tmp的最后一个元素加入新链表表尾

（8）将新链表复制给tmp链表

2.7.35 Code136 只出现一次的数字

（1）遍历数组

（2）当前数与第一个数异或，并赋值给第一个数

（3）返回第一个数值

2.7.36 Code137 只出现一次的数字II

思路：

 seenOnce = ~seenTwice & (seenOnce ^ num);

 seenTwice = ~seenOnce & (seenTwice ^ num);

2.7.37 Code149 直线上最多的点数

思路：

· 初始化最大点数 max_count = 1 。

· 迭代从 0 到 N - 2 所有的点 i 。

    · 对于每个点 i 找出通过该点直线的最大点数 max_count_i：

        · 初始化通过点 i 直线的最大点数：count = 1 。

        · 迭代下一个顶点 j 从 i+1 到 N-1 。

            · 如果 j 和 i 重合，更新点 i 相同点的个数。

            · 否则：

                · 保存通过 i 和 j 的直线。

                · 每步更新 count 。

        · 返回结果 max_count_i = count + duplicates 。

    · 更新结果 max_count = max(max_count, max_count_i) 。

2.7.38 Code150 逆波兰表达式求值

后缀表达式

（1）定义栈

（2）遍历字符串数组

（3）若当前字符串不是符号，入栈

（4）否则，弹出栈顶的两个操作数

（5）根据当前符号进行运算，并将结果入栈

（6）返回栈顶元素

2.8 贪心算法

2.8.1 Code011 盛最多水的容器

思路：两线段之间形成的区域总是会受到其中较短那条长度的限制。此外，两线段距离越远，得到的面积就越大。

    我们在由线段长度构成的数组中使用两个指针，一个放在开始，一个置于末尾。 此外，我们会使用变量 maxareamaxarea 来持续存储到目前为止所获得的最大面积。 在每一步中，我们会找出指针所指向的两条线段形成的区域，更新 maxareamaxarea，并将指向较短线段的指针向较长线段那端移动一步。

（1）定义两个指针指示左右两端

（2）定义最大面积变量，初始化为0

（3）迭代，迭代条件为左指针小于右指针

（4）计算当前面积，比较并更新最大面积变量

（5）将左右指针中较小的指针移动一位

2.8.2 Code012 整数转罗马数字

思路：贪心算法每次选择能表示的最大值，把对应的字符串联起来

（1）定义一个整数数组（从大到小排序）和一个字符串数组，将当前已知的对应关系保存下来

（2）定义一个StringBuffer变量，方便在遍历中保存结果

（3）迭代，迭代条件：当前下标不越界

（4）子迭代，停止条件，当前整数数组值不大于当前目标数

（5）将每个值对应的罗马字符串保存到strbuff

（6）目标数减去当前数组的值

（7）子迭代结束，下标+1

2.8.3 Code045 跳跃游戏II

思路：通过局部最优解得到全局最优解的贪心算法。遍历数组，不断更新最远距离。

2.8.4 Code055 跳跃游戏

思路：贪心算法，同上

2.8.5 Code134 加油站

思路：贪心算法

· 若从加油站A出发，恰好无法到达加油站C（只能到达C的前一站）。则A与C之间的任何一个加油站B均无法到达C

· 若储油量总和sum(gas) >= 耗油量总和sum(cost)，则问题一定有解

（1）定义变量total，总储油量减去总耗油量

（2）定义临时变量cur

（3）定义出发加油站编号start

（4）遍历数组

（5）当前位置油量减去消耗,加到total和cur

（6）若当前油量小于消耗

（7）起始站+1

（8）遍历结束，若total小于0，则返回-1，否则返回start

2.8.6 Code135分发糖果

思路：

· 先从左至右遍历学生成绩 ratings，按照以下规则给糖，并记录在 left数组 中：

    · 先给所有学生 1 颗糖；

    · 若 ratings_i>ratings_{i-1}，则第 i 名学生糖比第i−1 名学生多 1 个。

    · 若 ratings_i<=ratings_{i-1}，则第 i 名学生糖数量不变。（交由从右向左遍历时处理。）

    · 经过此规则分配后，可以保证所有学生糖数量 满足左规则 。

· 同理，在此规则下从右至左遍历学生成绩并记录在 right数组 中，可以保证所有学生糖数量 满足右规则 。

· 最终，取以上 2 轮遍历 left 和 right 对应学生糖果数的 最大值 ，这样则 同时满足左规则和右规则 ，即得到每个同学的最少糖果数量。

（1）定义左右数组，并初始化1

（2）从左到右遍历原数组

（3）当前数大于前面时，left数组当前值是前一个值+1

（4）从右到左遍历原数组

（5）若当前数大于后一个数，right数组当前值是后一个值+1

（6）选举左右数组中的最大值相加，结果返回

2.9 BFS

2.9.1 Code127 单词接龙