线性回归原理与python实现

机器学习

第一章：机器学习基础 第二章：线性回归 第三章：逻辑回归 第四章：BP 神经网络 第五章：卷积神经网络 第六章：循环神经网络 第七章：决策树与随机森林 第八章：支持向量机 第九章：隐马尔科夫 第十章：聚类等算法 ...

---

包括单变量线性回归和多变量线性回归

线性回归github地址

---

前言

机器学习是从人工智能中产生的一个重要学科分支，是实现智能化的关键

---

一、基础概念

回归分析（Regression Analysis)是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法 ，是一种预测性的建模技术

1.1 线性回归

线性回归，简单而言，就是将输入项分别乘以一些常量，再将结果加起来得到输出。线性回归包括一元线性回归和多元线性回归。

1.1.1 单变量线性回归

线型回归分析中，如果仅有一个自变量与一个因变量，且其关系大致上可用一条直线表示，则称之为简单回归分析。
如果发现因变量Y和自变量X之间存在高度的正相关，可以确定一条直线的方程，使得所有的数据点尽可能接近这条拟合的直线。简单回归分析的模型可以用以下方程表示：
Y=a+bx
其中：Y为因变量，a为截距，b为相关系数，x为自变量。

1.1.2 多变量线性回归

多元线性回归是简单线性回归的推广，指的是多个因变量对多个自变量的回归。其中最常用的是只限于一个因变量但有多个自变量的情况，也叫多重回归。多重回归的一般形式如下：

a代表截距，b1，b2，…，bk为回归系数。

二、单变量线性回归练习

2.1 吴恩达单变量线性回归作业

# 开发时间 ；2021/5/12 0012 15:04

#导入库
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

#导入数据集
#note:ex1data1.txt包含我们的线性回归问题的数据集。
# 第一列是一个城市的人口第二列是该城市一辆快餐车的利润。
# 利润为负数表示亏损。
data=pd.read_csv('F:\\ML\\线性回归\\数据文件\\ex1data1.txt',header=None,names=['population','profit'])
# print(data.head(5))

#画出预先散点图
data.plot(x='population',y='profit',kind='scatter',figsize=(16,9))
plt.show()

#代价函数
def cost_fun(X,y,theta):
     inner=(np.dot(X,theta)-y)**2
     m=len(X)
     return np.sum(inner)/2*m
#令x0=1
data.insert(0,'Ones',1)
# print(data)
X=data.iloc[:,:-1].values
print(X)
y=data.iloc[:,-1].values
#初始化theta
theta=np.zeros(X.shape[1])


#梯度下降
def gradient(X,y,alpha,theta):
    m = len(X)
    for i in range(1000):
        theta=theta-(alpha/m)*np.dot(X.T,(np.dot(X,theta)-y))
    return theta

theta=gradient(X,y,0.01,theta)
print(theta)
fig = plt.figure()
ax= plt.axes(projection='3d')
# fig,ax=plt.subplots(figsize=(16,9))
x=np.linspace(data.population.min(),data.population.max(),100)#设置x轴数据集，显示population的min->max,显示100个点
y=theta[0]+theta[1]*x
ax.plot(x,y,'r',label='Prediction')
ax.scatter(data.population,data.profit,label='Traning Data')#画点
ax.legend(loc=2)##点和线的图例，2表示在左上角。不写这句的话图例出现不了
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('single_linear_regression')
plt.show()

可视化数据

拟合效果

2.2 房价预测

# 开发时间 ；2021/5/4 0004 21:38
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn import datasets,linear_model

def data(file_name):
    data=pd.read_csv(file_name)
    X=[]
    Y=[]
    for single_square_feet,single_price_value in zip(data['square_feet'],data['price']):
        #遍历数据
        X.append([float(single_square_feet)])
        Y.append(float(single_price_value))
    return X,Y

#将数据拟合到线性模型
def linear_model_main(X,Y,predict_value):
    '''
    :param X_parameters:平方英尺
    :param Y_parameters:一平方英尺单价
    :param predict_value:预测值
    :return:
    '''
    #创建线性回归对象
    regression=linear_model.LinearRegression()#建立线性回归模型
    regression.fit(X,Y)#训练模型
    predict_outcome=regression.predict(predict_value)#预测结果
    predictions={}
    predictions['intercept']=regression.intercept_#相当于y=ax+b中的b,截距
    predictions['coefficient'] = regression.coef_#相当于y=ax+b中的a，系数
    predictions['predicted_value']=predict_outcome
    return predictions

X,Y=data('input_data.csv')
predictvalue=[[700]]
result=linear_model_main(X,Y,predictvalue)
print("Intercept value",result['intercept'])
print("coefficient",result['coefficient'])
print("predicted value",result['predicted_value'])
print('此模型为：','Y =',result['coefficient'],'* X +',result['intercept'])

#可视化
def show_linear_line(X,Y):
        regression=linear_model.LinearRegression()
        regression.fit(X,Y)
        plt.scatter(X,Y,color='blue')
        plt.plot(X,regression.predict(X),color='red',linewidth=4)
        plt.xticks(())
        plt.yticks(())
        plt.show()
show_linear_line(X,Y)

三、多变量线性回归练习

3.1 吴恩达多变量线性回归练习（版本一）

# 开发时间 ；2021/5/13 0013 13:24
#房价预测

#加载库
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

#加载数据集
#第一列是房子的大小（平方英尺），第二列是卧室的数量，第三列是房子的价格。
data=pd.read_csv('F:\\ML\\线性回归\\数据文件\\ex1data2.txt',names=['size','num_bedroom','price'],header=None)
#print(data.head(5))
'''
   size  num_bedroom   price
0  2104            3  399900
1  1600            3  329900
2  2400            3  369000
3  1416            2  232000
4  3000            4  539900
'''


#归一化处理
'''
特征缩放/归一化
对于多特征的机器学习问题，如果这些特征的取值在相近的范围内，则梯度下降法就能更快的收敛。
例如，考虑取值范围相差较大的两个特征的情况，损失函数等值线将呈现出扁椭圆形，相差倍数越大，椭圆越扁。
在这样的等值线上运行梯度下降，需要花很长一段时间，并可能来回波动，最终收敛到全局小值。
改善这一状况的有效做法是特征缩放，使两个特征的取值范围靠近。此时损失函数等值线更接近圆，
从数学上可以证明，梯度下降会找到一条更直接的路径（迭代次数减少）通向全局最小值。
常用方法：除最大值，均值归一化等。

在此实例中，房子的大小大约是卧室数量的1000倍。当特征有不同的数量级时，首先执行特征缩放可以使梯度下降收敛得更快。
'''
data=(data-data.mean())/data.std()
#print(data.head(5))
'''
       size  num_bedroom     price
0  0.130010    -0.223675  0.475747
1 -0.504190    -0.223675 -0.084074
2  0.502476    -0.223675  0.228626
3 -0.735723    -1.537767 -0.867025
4  1.257476     1.090417  1.595389
'''
data.insert(0,'Ones',1) # 就是在第一列[0] 添加名字为Ones的一列数据，数值都是1
X=data.iloc[:,:-1]#所有行，不取倒数第一列
# y=data.iloc[:,3:4]
y=data.iloc[:,-1]
theta=np.zeros(X.shape[1])
m=len(X)
alpha=0.01
#代价函数

def Cost_function(X,y,theta):
    inner=(np.dot(X,theta)-y)**2
    return np.sum(inner)/2*m

#梯度下降
def gradient(X,y,theta):
    i=0
    for i in range(1000):
        i+=1
        theta=theta-(alpha/m)*np.dot(X.T,(np.dot(X,theta)-y))
    return theta

theta=gradient(X,y,theta)
print(theta)

3.2 吴恩达多变量线性回归练习（版本二）

import pandas
import numpy as np
import matplotlib.pyplot as plt


def normalization(X):
    '''
    归一化
    :param X:
    :return:
    '''
    mu = np.mean(X, axis=0)
    # ddof的设置，会改变标准差的结算结果，因为总体误差和样本误差的计算公式不一样
    #标准差
    sigma = np.std(X, axis=0, ddof=1)
    X_norm = (X-mu)/ sigma
    return X_norm, mu, sigma


def computeCostMulti(X, y, theta):
    """
    计算损失函数
    :param X:
    :param y:
    :param theta:
    :return:
    """
    m = X.shape[0]
    costs = X.dot(theta) - y
    total_cost = costs.transpose().dot(costs) / (2 * m)
    return total_cost[0][0]


def gradientDescentMulti(X, y, theta, alpha, iterNum):
    """
    梯度下降实现
    :param X:
    :param y:
    :param theta:
    :param alpha:
    :param iterNum:
    :return:
    """
    m = len(X)

    J_history = list()

    for i in range(0, iterNum):
        costs = X.dot(theta) - y
        theta = theta - np.transpose(costs.transpose().dot(X) * (alpha / m))

        J_history.append(computeCostMulti(X, y, theta))

    return theta, J_history


def learningRatePlot(X_norm, y):
    """
    不同学习速率下的梯度下降比较
    :param X_norm:
    :param y:
    :return:
    """
    colors = ['b', 'g', 'r', 'c', 'm', 'y', 'k']
    plt.figure()
    iter_num = 50
    # 如果学习速率取到3，损失函数的结果随着迭代次数增加而发散，值越来越大，不太适合在同一幅图中展示
    for i, al in enumerate([0.01, 0.03, 0.1, 0.3, 1]):
        ta = np.zeros((X_norm.shape[1], 1))
        ta, J_history = gradientDescentMulti(X_norm, y, ta, al, iter_num)

        plt.plot([i for i in range(len(J_history))], J_history, colors[i], label=str(al))

    plt.title("learning rate")
    plt.legend()
    plt.show()


def normalEquation(X, y):
    """
    正规方程实现
    :param X:
    :param y:
    :return:
    """
    return np.linalg.inv(X.transpose().dot(X)).dot(X.transpose()).dot(y)


if __name__ == '__main__':
    # 读取数据
    data_path = r'F:\\ML\\线性回归\\数据文件\\ex1data2.txt'
    data = pandas.read_csv(data_path, delimiter=",", header=None)

    # 切分特征和目标， 注意：索引是从0开始的
    X = data.iloc[:, 0:2].values
    y = data.iloc[:, 2:3].values

    # 数据标准化
    X_norm, mu, sigma = normalization(X)

    ones = np.ones((X_norm.shape[0], 1))

    # 假设函数中考虑截距的情况下，给每个样本增加一个为1的特征
    X_norm = np.c_[ones, X_norm]

    # 初始化theta
    theta = np.zeros((X_norm.shape[1], 1))

    # 梯度下降学习速率为0.01
    alpha = 0.01
    # 梯度下降迭代次数为400
    iterNum = 400

    # 梯度下降
    theta, J_history = gradientDescentMulti(X_norm, y, theta, alpha, iterNum)

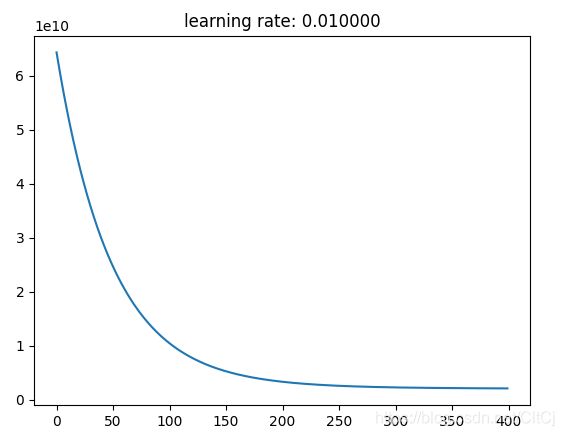
    # 画出梯度下降过程中的收敛情况
    plt.figure()
    plt.plot([i for i in range(len(J_history))], J_history)
    plt.title("learning rate: %f" % alpha)
    plt.show()

    # 使用不同学习速率下的收敛情况
    learningRatePlot(X_norm, y)

    # 预测面积为1650，卧室数量为3的房子价格
    x_pre = np.array([1650, 3])

    x_pre_norm = (x_pre - mu) / sigma
    numpy_ones = np.ones((1,))
    x_pre_norm = np.concatenate((np.ones((1,)), x_pre_norm))
    price = x_pre_norm.dot(theta)
    print("通过梯度下降求解的参数预测面积1650、卧室数量3的房子价格为：%f" % price[0])

    # 下面使用正规方程计算theta
    X_ = np.c_[ones, data.iloc[:, 0:2].values]
    y_ = data.iloc[:, 2:3].values

    theta = normalEquation(X_, y)

    # 预测面积为1650，卧室数量为3的房子价格
    x_pre = np.array([1, 1650, 3])
    price = x_pre.dot(theta)
    print("通过正规方程求解的参数预测面积1650、卧室数量3的房子价格为：%f" % price[0])
   

通过梯度下降求解的参数预测面积1650、卧室数量3的房子价格为：289314.620338
通过正规方程求解的参数预测面积1650、卧室数量3的房子价格为：293081.464335

3.2 股票预测

#数据获取
#从大型数据网站www.quandl.com获取
#开盘价open 最高价high 最低价low 收盘价close 交易额volume 调整后的开盘价Adj.Open 最高价Adj.High 最低价Adj.Low 收盘价Adj.Close 交易额Adj.volume
# 1 关于Quandl
# Quandl是为投资专业人士提供金融，经济和替代数据的首选平台，拥有海量的经济和金融数据。
#
# 2 Quandl模块
# Python有Quandl模块，通过Quandl模块可直接使用平台上的数据。Quandl包可以访问平台上所有免费的数据，但不是所有的数据都是免费的，部分数据需要付费才能使用。
import quandl
from sklearn import preprocessing
df=quandl.get('WIKI/GOOGL')#预测Google股票再用
#df=quandl.get('WIKI/AAPL')
import math
import numpy as np
#定义预测列变量，它存放研究对象的标签名
forecast_col='Adj. Close'
#定义预测天数，这里设置为所有数据量长度的1%
forecast_out=int(math.ceil(0.01*len(df)))
#只用到df中的下面几个字段
df=df[['Adj. Open','Adj. High','Adj. Low','Adj. Close','Adj. Volume']]
#构造两个新的列
#HL_PCT为股票最高价与最低价的变化百分比
df["HL_PCT"]=(df['Adj. High']-df['Adj. Close'])/df['Adj. Close']*100.0
#PCT_change为股票收盘价与开盘价的变化百分比
df["PCT_change"]=(df['Adj. Close']-df['Adj. Open'])/df['Adj. Open']*100.0
#因为sciket-learn并不会处理空数据，需要把为空的数据都设置为一个比较难出现的值，我们设置为-9999
df.fillna(-9999,inplace=True)
#用label代表该字段，是预测结果
#通过让Adj.Close列的数据往前移动1%行来表示
df['label']=df[forecast_col].shift(-forecast_out)
#最后生成真正在模型中使用的数据x,y,以及预测时用到的数据
X=np.array(df.drop(['label'],1))
X=preprocessing.scale(X)
# 上面生成label列时留下的最后1%行的数据，这些行并没有label数据，因此我们可以拿他们作为预测时用到的输入数据
X_lately = X[-forecast_out:]
X=X[:-forecast_out:]
#抛弃label列中为空的那些行
df.dropna(inplace=True)
y=np.array(df['label'])

from sklearn import model_selection,svm
from sklearn.linear_model import LinearRegression
# 开始前，先X和y把数据分成两部分，一部分用来训练，一部分用来测试
X_train,X_test,y_train,y_test=model_selection.train_test_split(X,y,test_size=0.25)
#生成线性回归对象
clf=LinearRegression(n_jobs=-1)
#开始训练
clf.fit(X_train,y_train)
#用测试数据评估准确性
accuracy=clf.score(X_test,y_test)
#进行预测
forecast_set=clf.predict(X_lately)
print(forecast_set,accuracy)
import matplotlib.pyplot as plt
from matplotlib import style
import datetime
#修改matplotlib样式
style.use('ggplot')
one_day=86400
#在df中新建Rorecast列，用于存放预测结果的数据
df['Forecast'] = np.nan
# 取df最后一行的时间索引
last_date = df.iloc[-1].name
last_unix = last_date.timestamp()
next_unix = last_unix + one_day
# 遍历预测结果，用它往df追加行
# 这些行除了Forecast字段，其他都设为np.nan
for i in forecast_set:
    next_date = datetime.datetime.fromtimestamp(next_unix)
    next_unix += one_day
    # [np.nan for _ in range(len(df.columns) - 1)]生成不包含Forecast字段的列表
    # 而[i]是只包含Forecast值的列表
    # 上述两个列表拼接在一起就组成了新行，按日期追加到df的下面
    df.loc[next_date] = [np.nan for _ in range(len(df.columns) - 1)] + [i]

# 开始绘图
df['Adj. Close'].plot()
df['Forecast'].plot()
plt.legend(loc=4)
plt.xlabel('Date')
plt.ylabel('Price')
plt.show()

总结

这相当于我对于一个线性回归的实践的一个集合，代码和数据集都可以在我的github上找到。