本文是对 Swift Algorithm Club 翻译的一篇文章。
Swift Algorithm Club是 raywenderlich.com网站出品的用Swift实现算法和数据结构的开源项目,目前在GitHub上有18000+⭐️,我初略统计了一下,大概有一百左右个的算法和数据结构,基本上常见的都包含了,是iOSer学习算法和数据结构不错的资源。
andyRon/swift-algorithm-club-cn是我对Swift Algorithm Club,边学习边翻译的项目。由于能力有限,如发现错误或翻译不妥,请指正,欢迎pull request。也欢迎有兴趣、有时间的小伙伴一起参与翻译和学习。当然也欢迎加⭐️,。
本文的翻译原文和代码可以查看swift-algorithm-club-cn/Splay Tree
伸展树/分裂树(Splay Tree)
伸展树是一种数据结构,在结构上与平衡二叉搜索树相同。 在伸展树上执行的每个操作都会导致重新调整,以便快速访问最近运行的值。 在每次访问时,树被重新排列,并且使用一组特定的旋转将访问的节点移动到树的根,这些旋转一起被称为Splaying。
旋转
有3种类型的旋转可以形成Splaying:
- ZigZig
- ZigZag
- Zig
Zig-Zig
给定节点a,如果a不是根节点,a具有子节点b,并且a和b都是左子节点或右子节点,则按 Zig-Zig 执行。
案例两个节点都是右节点
案例两个节点都是左节点
重要的是要注意 ZigZig 首先执行中间节点与其父节点的旋转(称之为祖父节点),然后执行剩余节点(孙子节点)的旋转。 这样做有助于保持树平衡,即使它是通过插入一系列递增值来首次创建的(参见下面的最坏情况场景,然后解释为什么ZigZig首先旋转到祖父母)。
Zig-Zag
给定节点a,如果a不是根节点,并且a具有子节点b,并且b是a的左子节点,a本身是右子节点(相反的节点),则执行 Zig-Zag。
案例 右-左
译注: 上图中9是a,7是b
案例 左-右
重要的是ZigZag首先执行孙子节点的旋转,然后再次执行与其新父节点相同的节点。
Zig
当要旋转的节点a父节点是根节点时,执行Zig。
伸展
伸展 包括根据需要进行如此多的旋转,直到受操作影响的节点位于顶部并成为树的根节点。
while (node.parent != nil) {
operation(forNode: node).apply(onNode: node)
}
操作返回要应用的所需旋转。
public static func operation(forNode node: Node) -> SplayOperation {
if let parent = node.parent, let _ = parent.parent {
if (node.isLeftChild && parent.isRightChild) || (node.isRightChild && parent.isLeftChild) {
return .zigZag
}
return .zigZig
}
return .zig
}
在应用阶段,算法根据要应用的旋转确定涉及哪些节点,并继续用其父节点重新排列节点。
public func apply(onNode node: Node) {
switch self {
case .zigZag:
assert(node.parent != nil && node.parent!.parent != nil, "Should be at least 2 nodes up in the tree")
rotate(child: node, parent: node.parent!)
rotate(child: node, parent: node.parent!)
case .zigZig:
assert(node.parent != nil && node.parent!.parent != nil, "Should be at least 2 nodes up in the tree")
rotate(child: node.parent!, parent: node.parent!.parent!)
rotate(child: node, parent: node.parent!)
case .zig:
assert(node.parent != nil && node.parent!.parent == nil, "There should be a parent which is the root")
rotate(child: node, parent: node.parent!)
}
}
伸展树上的操作
插入
要插入值:
- 将其插入二叉搜索树中
- 将值显示到根目录
删除
删除值:
- 在二叉搜索树中删除
- 将已删除节点的父节点放到根节点
搜索
要搜索值:
- 在二叉搜索树中搜索它
- 将包含值的节点放到根目录
- 如果未找到,则展开将成为搜索值的父节点的节点
最小和最大
- 在树中搜索所需的值
- 将节点放到根节点
例子
例子 1
The sequence of steps will be the following:
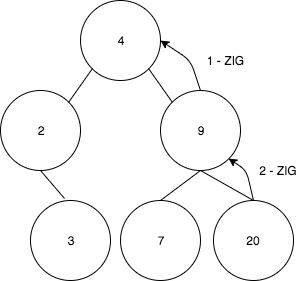
让我们假设执行find(20)操作,现在需要将值20显示到根节点。
步骤顺序如下:
- 当我们使用ZigZig时,我们需要旋转9到4。
- 第一次旋转后,我们得到下面树:
- 最后把20旋转到9
例子 2
现在假设执行了insert(7)操作,我们处于ZigZag情况。
- 首先7旋转到9
- 结果为:
- 最后7旋转到4
优点
伸展树提供了一种快速访问经常请求的元素的有效方法。这个特性让下面实现有了一个很好的选择,例如高速缓存或垃圾收集算法,或涉及从数据集频繁访问特定数量的元素的任何其他问题。
缺点
伸展树总是不完美平衡,因此在以递增顺序访问树中的所有元素的情况下,树的高度变为n。
时间复杂度
| Case | Performance |
|---|---|
| 平均 | O(log n) |
| 最差 | n |
n是树中的项数。
最糟糕案例表现的一个例子
假设在伸展树中插入了一系列连续值。我们以[1,2,3,4,5,6,7,8]为例。
树的结构如下:
- 插入数字 1
- 插入 2
- 伸展 2 到根节点
- 插入 3
- 伸展 3 到根节点
- 插入 4
- 插入其余值后,树将如下所示:
如果我们按照相同的顺序保持插入编号,则该树变得不平衡并且高度为n,n是插入的值的数量。
获取此树后,find(1)操作将采用O(n)
ZigZig旋转顺序:首先祖父节点
但是由于伸展树 的属性和find(1)操作后的ZigZig旋转,树再次变得平衡。只有当我们考虑ZigZig旋转的顺序,并且首先发生对祖父节点的旋转时,才会发生这种情况。
ZigZigs 旋转的顺序如下所示:
- Rotate 2 to 3
- Rotate 1 to 2
- Rotate 4 to 5
- Rotate 1 to 4
- 最后将1伸展到根节点之后,树将如下所示:
基于上面的例子,我们可以看出为什么首先旋转祖父节点是很重要的。 我们从一棵 height = 8 的初始树得到一棵 height = 6 的树。如果树高了,我们通过伸展操作后,可以几乎得到初始高度一半的树。
ZigZig错误的旋转顺序
如果旋转首先是父节点而不是祖父节点,我们将完成以下不平衡的树,只是反转原树元素。
扩展阅读
伸展树的维基百科
加州大学伯克利分校的伸展树课程CS 61B Lecture 34
作者:Martina Rodeker
翻译:Andy Ron
校对:Andy Ron