非监督学习,sklearn聚类,降维,决策树
1. 聚类
聚类:对数据集进行分类,比如y=0,y=1,y=2等
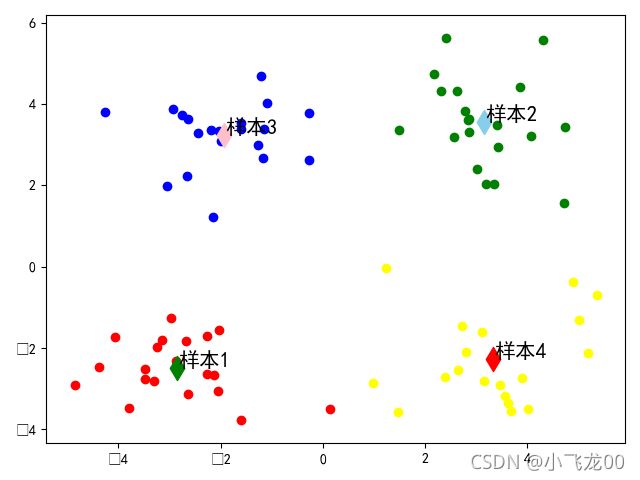
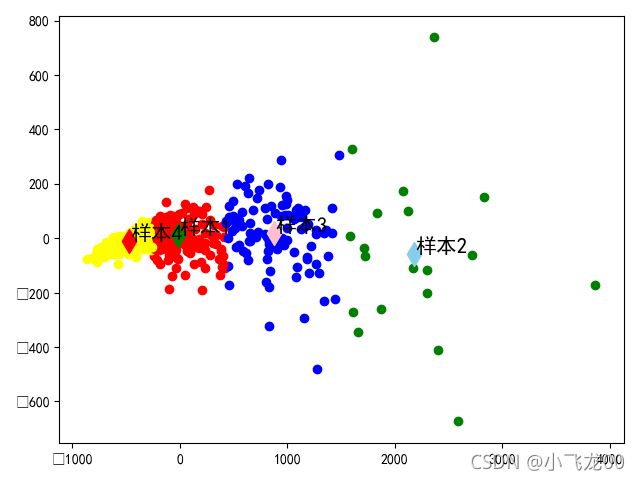
1.1 kmeans聚类(k=4)
聚类:分为四类,所以K=4
from sklearn.cluster import KMeans
import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
# k-means
# k均值聚类算法
# 1.导入聚类包 from sklearn.cluster import k_means
# 2.加载数据集test.txt
data=np.loadtxt(r'E:\机器学习\机器学习1\机器\聚类\test .txt',delimiter='\t')
print(data)
# 3.数据预处理
def suofang(x):
xmin=np.min(x,axis=0)
xmax=np.max(x,axis=0)
s=x-xmin/(xmax-xmin)
return s
data=suofang(data)
# print(data)
# 4.调库实例化对象
# 4.1训练模型 fit K=2
model=KMeans(n_clusters=4)
model.fit(data)
# 5.输出 预测值,代价,索引,聚类中心点
print('聚类中心点',model.cluster_centers_)
print('预测',model.predict(data))
print('聚类索引位置',model.labels_)
print('聚类中心的个数',model.n_clusters)
print('损失函数',model.inertia_)
# 6.画出分类后的图,加上注释。
#画样本点
for i in range(len(data)):
if model.labels_[i]==0:
plt.scatter(data[i,0],data[i,1],c='red')
elif model.labels_[i]==1:
plt.scatter(data[i,0],data[i,1],c='green')
elif model.labels_[i]==2:
plt.scatter(data[i,0],data[i,1],c='blue')
else:
plt.scatter(data[i, 0], data[i, 1], c='yellow')
#画聚类中心点
m=model.cluster_centers_
plt.scatter(m[0,0],m[0,1],c='green',s=150,marker='d')
plt.scatter(m[1,0],m[1,1],c='skyblue',s=150,marker='d')
plt.scatter(m[2,0],m[2,1],c='pink',s=150,marker='d')
plt.scatter(m[3,0],m[3,1],c='red',s=150,marker='d')
#文本注释
for i in range(4):
plt.annotate(str('样本')+str(i+1),xy=(m[i,0],m[i,1]),xytext=(1,1),
textcoords=('offset points'),fontsize=15)
plt.show()
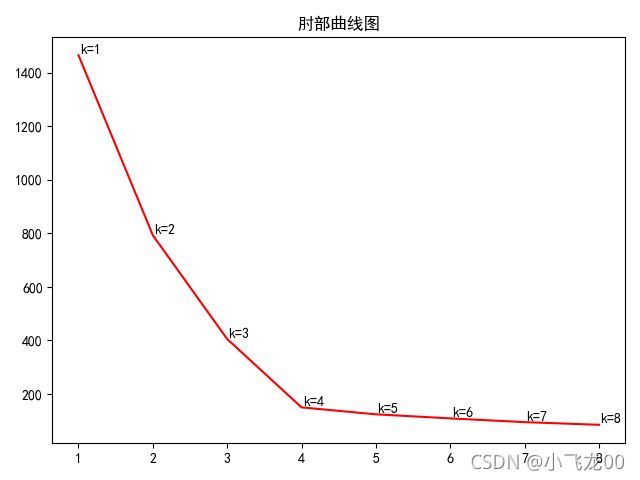
# 7.画出肘部法则的图,选取最优聚类中心个数。
#画肘部法则图
k=[]
loss=[]
for i in range(8):
model=KMeans(n_clusters=i+1)
model.fit(data)
k.append(i+1)
loss.append(model.inertia_)
plt.title('肘部曲线图')
plt.plot(k,loss,c='red')
print('loss=',loss)
#文本注释
for i in range(8):
plt.annotate(str('k=')+str(i+1),xy=(k[i],loss[i]),
xytext=(1,1),textcoords=('offset points'))
plt.show()
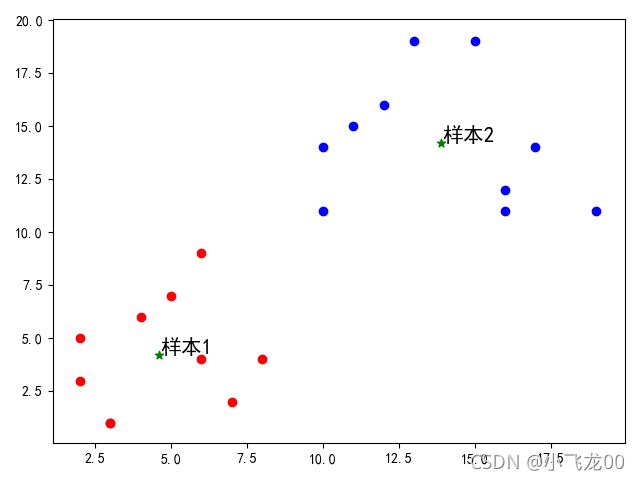
1.2. kmeans聚类(k=2)
聚类:分为两类,所以K=2
from sklearn.cluster import KMeans#cluster:使聚集
import matplotlib.pyplot as plt
import numpy as np
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
# 生成20个数据
data = np.array([[2,5],[4,6],[3,1],[6,4],[7,2],[8,4],[2,3],[3,1],[5,7],[6,9],[12,16],[10,11],[15,19],[16,12],[11,15],[10,14],[19,11],[17,14],[16,11],[13,19]])
model=KMeans(n_clusters=2)
model.fit(data)#拟合模型
print("聚类中心的个数:",model.n_clusters)
print("预测值:",model.predict(data))
print("数据索引位置=",model.labels_)#数据索引位置
print('损失函数=',model.inertia_)#损失函数
print('聚类中心点=',model.cluster_centers_)
#画样本点
for i in range(len(data)):
if (model.labels_[i]==0):
plt.scatter(data[i,0],data[i,1],c='r')
else:
plt.scatter(data[i, 0], data[i, 1], c='b')
#画聚类中心点
plt.scatter(model.cluster_centers_[0,0],model.cluster_centers_[0,1],c='g',marker='*')
plt.scatter(model.cluster_centers_[1,0],model.cluster_centers_[1,1],c='g',marker='*')
#plt.show()
#文本注释
for i in range(2):
plt.annotate(str('样本')+str(i+1),xy=(model.cluster_centers_[i,0],model.cluster_centers_[i,1]),
xytext=(1,1),textcoords=('offset points'),fontsize=15)
plt.show()
#画肘部法则图
K=[]
loss=[]
for i in range(len(data)):
model=KMeans(n_clusters=i+1)
model.fit(data)
K.append(i+1)#k-->[1,2,3,4,-----]
loss.append(model.inertia_)#迭代损失值
plt.figure()
plt.title('肘部曲线图')
plt.plot(K,loss,c='r')
##文本注释
for i in range(len(data)):
plt.annotate(str('k=')+str(i+1),xy=(K[i],loss[i]),xytext=(10,10),textcoords=('offset points'))
plt.show()
1.3 先降维再聚类
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris,load_breast_cancer
from sklearn.decomposition import PCA
import warnings
warnings.filterwarnings('ignore')
from sklearn.cluster import KMeans
plt.rcParams['font.sans-serif'] = ['SimHei']
# 调用乳腺癌数据集,对特征矩阵进行降维与聚类
data1=load_breast_cancer()
x=data1.data
y=data1.target
print(x)
print(y)
# e)创建pca降维模型,保留两个特征
pca=PCA(n_components=2)
pca.fit(x,y)
newx=pca.transform(x)
print(newx)
# f)对特征矩阵进行降维
# g)导包画图显示中文及负号
# h)对降维后的特征进行聚类操作
kms=KMeans(n_clusters=2)
kms.fit(x)
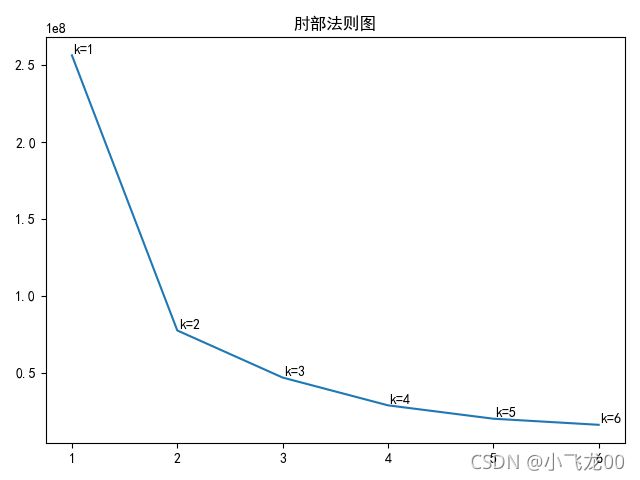
# i)画出肘部法则图
k=[]
loss=[]
for i in range(len(data1)):
kms=KMeans(n_clusters=i+1)
kms.fit(newx)
k.append(i+1)
loss.append(kms.inertia_)
plt.plot(k,loss)
plt.title('肘部法则图')
# plt.show()
for i in range(len(data1)):
plt.annotate(str('k=')+str(i+1),xy=(k[i],loss[i]),
xytext=(1,1),textcoords=('offset points'))
plt.show()
# j)选择出最优k值
print(k)
# k)创建kmeans模型并拟合数据
kms=KMeans(n_clusters=4)
kms.fit(newx)
# l)画出分类后的样本点,并根据标签上色分类
for i in range(len(newx)):
if kms.labels_[i]==0:
plt.scatter(newx[i,0],newx[i,1],c='red')
elif kms.labels_[i]==1:
plt.scatter(newx[i,0],newx[i,1],c='green')
elif kms.labels_[i]==2:
plt.scatter(newx[i,0],newx[i,1],c='blue')
else:
plt.scatter(newx[i, 0], newx[i, 1], c='yellow')
# m)画出聚类中心
m=kms.cluster_centers_
print(m)
plt.scatter(m[0,0],m[0,1],c='green',s=150,marker='d')
plt.scatter(m[1,0],m[1,1],c='skyblue',s=150,marker='d')
plt.scatter(m[2,0],m[2,1],c='pink',s=150,marker='d')
plt.scatter(m[3,0],m[3,1],c='red',s=150,marker='d')
for i in range(4):
plt.annotate(str('样本')+str(i+1),xy=(m[i,0],m[i,1]),
xytext=(1,1),textcoords=('offset points'),fontsize=15)
plt.show()
1.4 kmeans底层(质心计算过程)
#质心计算过程
import numpy as np
import matplotlib.pyplot as plt
# 样本集
#X= np.array([[2,5],[4,6],[3,1],[6,4],[7,2],[8,4],[2,3],[3,1],[5,7],[6,9],[12,16],[10,11],[15,19],[16,12],[11,15],[10,14],[19,11],[17,14],[16,11],[13,19]])
X = np.array([[1, 2], [2, 2], [6, 8], [7, 8]])
#定义初始化质心
C = np.array([[1.0, 2.0], [2.0, 8.0]])##定义初始化聚类中心点
#重复计算质心5次
iters = 5
while (iters>0) :
iters -= 1
B = [] #每个样本点到聚类中心的距离
for c in C:#第一次c=(1,2),第二次c=(2,8)
#计算每个点到质心的欧式距离
dis = np.sqrt(((X - c)**2).sum(axis=1))
#print(dis)
B.append(dis)#
#print('B=',B)
#求样本点属于哪一个类别
min_idx = np.argmin(np.array(B),axis=0)#=[0,1,1,0]##选村民,样本点选聚类中心的索引
print(min_idx)
for i in range(2):#样本点数[0.1]
#更换每个聚类中心的位置
C[i] = np.mean(X[min_idx == i],axis=0)
#打印所有样本的所属的簇
#print(min_idx)
print(C)
2. 降维
降维:对特征值进行降维,比如:(x1,x2,x3…xn)可以变为低维(a1,a2)
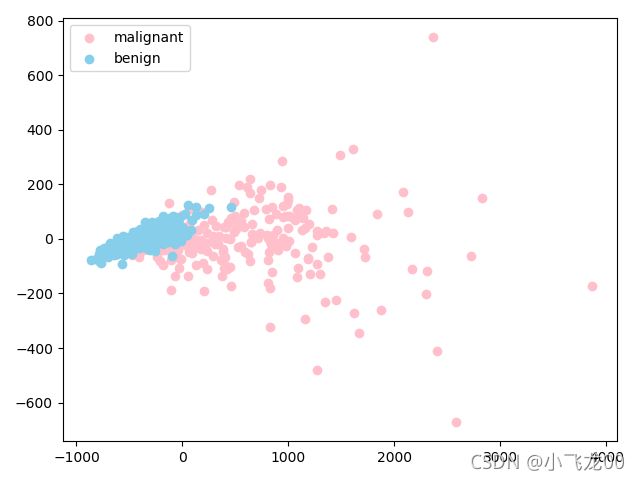
2.1 主成分分析(PCA)–乳腺癌数据集
#乳腺癌数据集
#1.导包
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
import sklearn.datasets as dts
from sklearn.model_selection import train_test_split
# 2.加载数据集
data=dts.load_breast_cancer()
x=data.data
y=data.target
# 3.数据预处理(缩放,洗牌,切分)
trainx,testx,trainy,testy=train_test_split(x,y,train_size=0.7,shuffle=True)
# 4.调库
model=PCA(n_components=2)#直接指定降维后要保留2个特征
# 5.拟合模型
model.fit(x)
# 6.输出:特征值方差,特征值比率,特征值向量,特征值维度。。。
print('特征向量:',model.components_)
print('特征值方差:',model.explained_variance_)
print('特征方差率:',model.explained_variance_ratio_)
print('特征向量的形状',model.components_.shape)
names=data.target_names
# 7.画降维后的数据散点图
x1=model.transform(x)
print(x1)
print(x1.shape)
print(y)
# 方法一:
# for i in range(len(x1)):
# if y[i]==0:
# plt.scatter(x1[i,0],x1[i,1],c='g')
# else:
# plt.scatter(x1[i,0],x1[i,1],c='b')
# 方法二
plt.scatter(x1[y==0,0],x1[y==0,1],c='pink',label=names[0])
plt.scatter(x1[y==1,0],x1[y==1,1],c='skyblue',label=names[1])
plt.legend(loc='upper left')
plt.show()
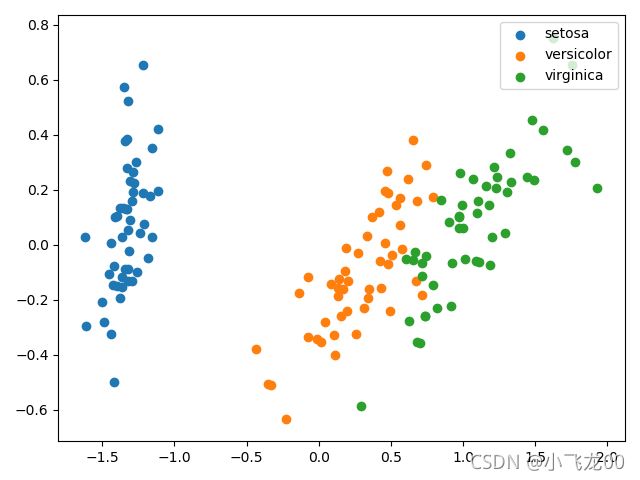
2.2 主成分分析(PCA)–iris数据集
import sklearn.datasets as dts
import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
from sklearn.decomposition import PCA
# 1.导入对应数据包 from sklearn.decomposition import PCA
data=dts.load_iris()
# 2.加载数据集
x=data.data
y=data.target
names=data.target_names
# print(x)
# print(y)
# 3.数据预处理(缩放,洗牌,切分)
def suofang(x):
miu=np.mean(x)
sigma=np.std(x)
s=(x-miu)/sigma
return s
x=suofang(x)
# print(x)
np.random.seed(4)
m,n=x.shape
order=np.random.permutation(m)
x=x[order]
y=y[order]
a=int(m*0.7)
trainx=x[:a]
trainy=y[:a]
testx=x[a:]
testy=y[a:]
print(y)
# 4.调库
model=PCA(n_components=2)
# print(model)
# 5.拟合模型
model.fit(trainx,trainy)
newx=model.transform(x)
# 6.输出:特征值方差,特征值比率,特征值向量,特征值维度。。。
print('特征值方差:',model.explained_variance_)
print('特征值比率:',model.explained_variance_ratio_)
print('特征值向量:',model.components_)
print('特征值维度:',model.components_.shape)
# 7.画降维后的数据散点图
print(newx)
plt.scatter(newx[y==0,0],newx[y==0,1],label=names[0])
plt.scatter(newx[y==1,0],newx[y==1,1],label=names[1])
plt.scatter(newx[y==2,0],newx[y==2,1],label=names[2])
plt.legend(loc='upper right')
plt.show()
3. 决策树(可以用于分类和回归)
3.1 决策树–乳腺癌数据集
import matplotlib.pyplot as plt
import sklearn.datasets as dts #数据集包
dts.load_breast_cancer()
import warnings
warnings.filterwarnings('ignore')
from sklearn.decomposition import PCA #导入降维包
from sklearn.model_selection import train_test_split #导入训练集测试集切分包
from sklearn.tree import DecisionTreeClassifier #导入决策树包
from sklearn.tree import DecisionTreeRegressor
plt.rcParams['font.sans-serif']= ['SimHei']
# 1.导入对应数据包
# 2.加载数据集
data1=dts.load_breast_cancer()
# print(data1)
x=data1.data
y=data1.target
print(x.shape)
print(y.shape)
# print(y)
# 2.用pca降维到2维
model1=PCA(n_components=2)
model1.fit(x,y)
# 2.数据预处理(缩放,洗牌,切分)
trainx,testx,trainy,testy=train_test_split(x,y,train_size=0.7,shuffle=True)
# 4.调库
newtrainx=model1.transform(trainx)
newtestx=model1.transform(testx)
# print(newtrainx)
# print(newtestx)
dtg1=DecisionTreeClassifier(max_depth=5)
dtg2=DecisionTreeClassifier(max_depth=2)
# 5.拟合模型
dtg1.fit(newtrainx,trainy)
dtg2.fit(newtrainx,trainy)
# 6.输出:精度和预测值
print('训练集精度为:',dtg1.score(newtrainx, trainy)*100,'%')
print('训练集精度为:',dtg1.score(newtestx, testy)*100,'%')
print('训练集精度为:',dtg2.score(newtrainx, trainy)*100,'%')
print('训练集精度为:',dtg2.score(newtestx, testy)*100,'%')
print(dtg1.predict(newtrainx))
print(dtg1.predict(newtestx))
# 7.画出特征分类图。
plt.plot(testy,testy,label='训练样本')
plt.scatter(testy,dtg1.predict(newtestx),c='r',label='测试样本')
plt.title('深度=5,准确率=%.2f'%(dtg1.score(newtrainx,trainy)*100)+'%')
plt.show()
3.2决策树–糖尿病数据集
import matplotlib.pyplot as plt
import numpy as np
from sklearn.decomposition import PCA #降维包
from sklearn.svm import SVR,SVC #支持向量机
from sklearn.model_selection import train_test_split #分割训练集和测试集包
from sklearn.datasets import load_iris,load_boston,load_diabetes,load_breast_cancer
from sklearn.cluster import KMeans,DBSCAN #聚类包
import sklearn.neural_network #神经网络包
from sklearn.tree import DecisionTreeRegressor,DecisionTreeClassifier #决策树包
from sklearn.linear_model import LinearRegression,LogisticRegression #线性回归和逻辑回归包
from sklearn.naive_bayes import GaussianNB #朴素贝叶斯
from sklearn.neighbors import KNeighborsClassifier,KNeighborsRegressor #k邻近算法
#1.加载数据集
data=load_diabetes()
x=data.data
y=data.target
print(x.shape)
print(y.shape)
#2.降维
model=PCA(n_components=2)
model.fit(x,y)
#转化为2个维度的新x
newx=model.transform(x)
print('特征向量:',model.components_)
print('特征方差率:',model.explained_variance_ratio_)
print('特征向量形状:',model.components_.shape)
print('特征方差:',model.explained_variance_)
# 3.切分训练集、测试集
trainx,testx,trainy,testy=train_test_split(newx,y,train_size=0.7,shuffle=True)
# 4.决策树调库
dtr=DecisionTreeRegressor(max_depth=3)
dtr.fit(trainx,trainy)
dtr1=DecisionTreeRegressor(max_depth=5)
dtr1.fit(trainx,trainy)
# 5.计算精确度
print('训练集精确度:',dtr.score(trainx, trainy)*100,'%')
print('测试集精确度:',dtr.score(testx, testy)*100,'%')
print('训练集精确度:',dtr1.score(trainx, trainy)*100,'%')
print('测试集精确度:',dtr1.score(testx, testy)*100,'%')
#画图
plt.scatter(trainx[:,0],trainy)
plt.scatter(trainx[:,1],trainy)
plt.show()
test.txt数据:
1.658985 4.285136
-3.453687 3.424321
4.838138 -1.151539
-5.379713 -3.362104
0.972564 2.924086
-3.567919 1.531611
0.450614 -3.302219
-3.487105 -1.724432
2.668759 1.594842
-3.156485 3.191137
3.165506 -3.999838
-2.786837 -3.099354
4.208187 2.984927
-2.123337 2.943366
0.704199 -0.479481
-0.392370 -3.963704
2.831667 1.574018
-0.790153 3.343144
2.943496 -3.357075
-3.195883 -2.283926
2.336445 2.875106
-1.786345 2.554248
2.190101 -1.906020
-3.403367 -2.778288
1.778124 3.880832
-1.688346 2.230267
2.592976 -2.054368
-4.007257 -3.207066
2.257734 3.387564
-2.679011 0.785119
0.939512 -4.023563
-3.674424 -2.261084
2.046259 2.735279
-3.189470 1.780269
4.372646 -0.822248
-2.579316 -3.497576
1.889034 5.190400
-0.798747 2.185588
2.836520 -2.658556
-3.837877 -3.253815
2.096701 3.886007
-2.709034 2.923887
3.367037 -3.184789
-2.121479 -4.232586
2.329546 3.179764
-3.284816 3.273099
3.091414 -3.815232
-3.762093 -2.432191
3.542056 2.778832
-1.736822 4.241041
2.127073 -2.983680
-4.323818 -3.938116
3.792121 5.135768
-4.786473 3.358547
2.624081 -3.260715
-4.009299 -2.978115
2.493525 1.963710
-2.513661 2.642162
1.864375 -3.176309
-3.171184 -3.572452
2.894220 2.489128
-2.562539 2.884438
3.491078 -3.947487
-2.565729 -2.012114
3.332948 3.983102
-1.616805 3.573188
2.280615 -2.559444
-2.651229 -3.103198
2.321395 3.154987
-1.685703 2.939697
3.031012 -3.620252
-4.599622 -2.185829
4.196223 1.126677
-2.133863 3.093686
4.668892 -2.562705
-2.793241 -2.149706
2.884105 3.043438
-2.967647 2.848696
4.479332 -1.764772
-4.905566 -2.911070