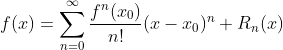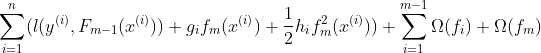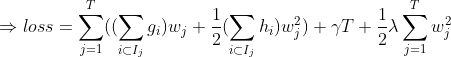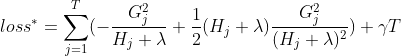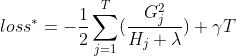机器学习--分类算法--集成学习算法理论(RF/AdaBoost/GBDT/XGBoost算法)
目录
一 集成学习背景
1 集成学习概念
2 集成学习优势
1)弱分类器之间存在差异性的问题
2)对于数据集过大或者过小的问题
3)对于数据集的划分边界过于复杂,线性模型很难描述的问题
4)对于多个异构数据集而言,数据集很难合并的问题
3 集成学习三种思想
1)Bagging思想(Bootstrap Aggregating,自主汇聚法)
2)Boosting思想(存在弱学习器,可通过提升技术变成强学习器)
3)Stacking思想
二 Bagging
1 随机森林算法(Random Forest)
1)算法原理
2)优点
3)缺点
2 随机森林的推广算法
1)Extra Tree算法原理(一般不推荐使用)
2)Totally Random Trees Embedding算法原理(TRTE,一种无监督的特征转换)
3)Isolation Forest算法原理(IForest,一种异常点检测算法)
三 Boosting思想
1 AdaBoost算法
1)概念(关注提升过程)
2)算法原理
3)算法流程
4)算法优缺点
2 GBDT(Gradient Boosting Dicision Tree)
1)算法概念
2)算法流程(以回归问题为例)
3)算法处理分类问题,损失函数采用对数损失函数(交叉熵损失函数)
4)算法优缺点
3 XGBOOST(GBDT的变种算法)
1)算法概念
2)算法原理
3)算法学习策略(树生成策略)
4)XGBoost特性(优点)
四 Stacking思想
一 集成学习背景
1 集成学习概念
指将若干个学习器进行组合而得到一个新的学习器
2 集成学习优势
1)弱分类器之间存在差异性的问题
导致分类边界的不同(换言之存在错误),那么将多个弱分类器合并之后,会得到更加合理的分类边界
2)对于数据集过大或者过小的问题
我们可以采用划分或者有放回操作,得到不同的数据子集,分别训练不同的学习器,在组合成一个新的学习器
3)对于数据集的划分边界过于复杂,线性模型很难描述的问题
可以训练多个学习器,再组合成一个新的学习器
4)对于多个异构数据集而言,数据集很难合并的问题
可以对每个数据集训练一个学习器,在组合成一个新的学习器
3 集成学习三种思想
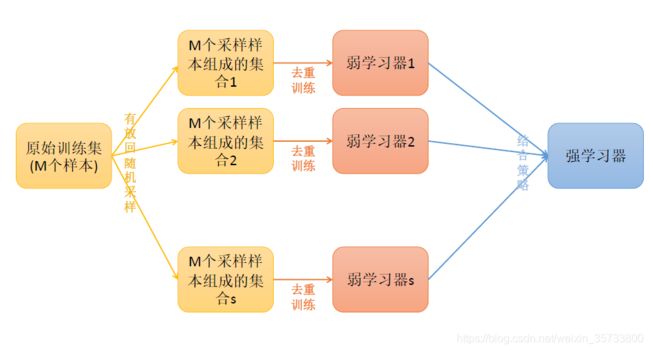
1)Bagging思想(Bootstrap Aggregating,自主汇聚法)
在原始数据集上![]() 通过bootstap有放回抽样方式,抽取出S个新的数据集
通过bootstap有放回抽样方式,抽取出S个新的数据集![]() (存在重复数据,实际训练时需去重),分别训练S个学习器,并进行组合成新的学习器(并行训练)
(存在重复数据,实际训练时需去重),分别训练S个学习器,并进行组合成新的学习器(并行训练)
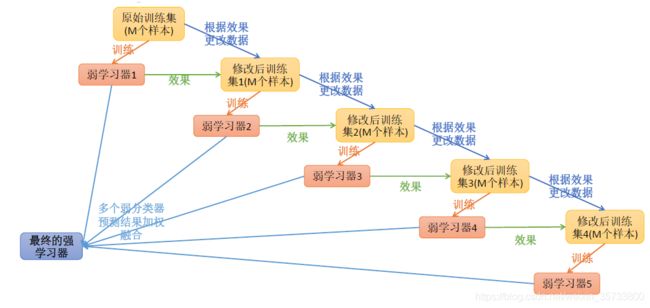
2)Boosting思想(存在弱学习器,可通过提升技术变成强学习器)
每一步产生弱学习器,并加权累计到总学习器上,且每一步的弱学习器生成都是依据损失函数的梯度方式(串行训练)
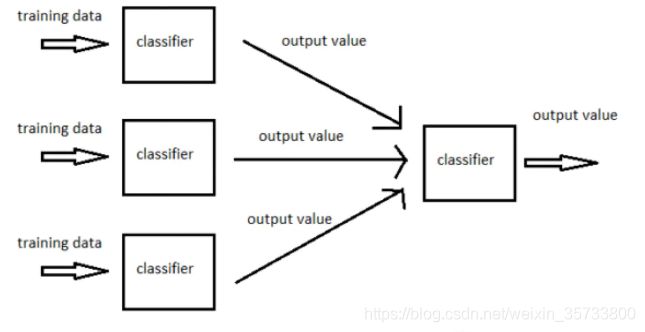
3)Stacking思想(堆叠+分阶段)
训练多个学习器产生多个输出,并作下个学习器的输入,并重复多个阶段进行(类似于深度学习中的神经网络)
注意:Bagging与Boosting区别
- 第一点:样本角度
Bagging每一轮样本是从原始数据中有放回随机抽取的
Boosting每一轮样本为原始数据,但是样本权重或者目标属性由上一轮损失函数调整
- 第二点:计算方式角度
Bagging采用并行计算
Boosting采用串行计算
- 第三点:泛化误差角度
Bagging降低的是模型的方差(![]() )
)
Boosting降低的是模型的偏差(![]() )
)
二 Bagging
1 随机森林算法(Random Forest)
1)算法原理
- 在原始数据集中采用自助法(Bootstrap)抽取出新数据集
- 从所有属性中随机抽取K个特征属性,再进行选择特征属性和分裂特征属性(纯度损失的度量)创建决策树
- 重复上述步骤S次,创建S个决策树
- 将S个决策树形成森林,通过平均值法或者多数表决法进行预测样本
2)优点
第一点:无需进行交叉验证或者使用一个独立测试集来获取误差的无偏估计(换言之它可以在内部进行误差的无偏估计)
- oob样本(袋外样本)
数据集足够大,采用bootstrap抽样,对于第K棵树而言,约有1/3总样本未参与第K棵树的生成,它们被称为第K棵树的袋外样本
- oob错误率(袋外错误率)
第一步:每个袋外样本,计算它作为袋外样本的树(约有1/3棵树),对其分类情况
第二步:多数表决法预测分类情况
第三步:使用误分类样本个数占总袋外样本的比率作为袋外错误率
第二点:可以得到特征重要度,进行特征选择
- 随机森林中一个特征被分割的次数越多,那么该特征重要度越高
 特征重要度 = #随机森林中具有该特征的内部节点总数 / #随机森林中具有该特征决策树的所有内部节点总数
特征重要度 = #随机森林中具有该特征的内部节点总数 / #随机森林中具有该特征决策树的所有内部节点总数
第三点:可以并行训练,对于大规模数据集具有训练优势
3)缺点
第一点:对于特别的异常样本,使得RF容易陷入过拟合
第二点:对于取值较多的特征,使得RF决策受到影响
2 随机森林的推广算法
1)Extra Tree算法原理(一般不推荐使用)
- 原始数据集不采用抽样方式,直接使用原始数据集
- 从所有特征属性中随机选择K个属性,再从K个属性随机选择特征属性以及分裂特征属性,创建树
- 重复上述步骤S次,创建S个树
- S个树形成森林,采用平均值法或者多数表决发,预测样本
注意:在某些特别情况下,可能优于RF算法
2)Totally Random Trees Embedding算法原理(TRTE,一种无监督的特征转换)
- 在原始数据集中采用自助法(Bootstrap)抽取出新数据集
- 计算所有特征属性的方差,从中选择方差最大的特征
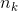 ,使用最大特征的方差中位数
,使用最大特征的方差中位数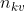 ,划分为两个分支,创建树
,划分为两个分支,创建树 - 重复上述步骤S次,创建S个树
- S个树形成森林,从而每个样本在每棵树上的叶子节点位置确定下来,将位置信息转换成向量即可
注意:是一种非监督的特征转换方式(RF+KD-Tree),可以将数据从低维度映射到高维度
3)Isolation Forest算法原理(IForest,一种异常点检测算法)
- 从原始数据集中,随机抽取少量样本数据形成新的数据集
- 从所有特征属性中随机选择K个属性,再从K个属性中随机选择特征属性以及分裂特征属性,创建树(深度一般不深)
- 重复上述步骤T次,形成T个树
- 将T个树形成森林,再将测试点
 拟合到T棵树上,进行异常点检测
拟合到T棵树上,进行异常点检测
第一步:计算该样本在T棵决策树上的叶子节点深度![]() ,求得平均深度
,求得平均深度![]()
第二步:m为样本个数,![]() 为欧拉常数:
为欧拉常数:
第三步:从而测试点![]() 作为异常点概率:
作为异常点概率:![]()
注意:异常点检测不需要太多样本以及太多决策树
三 Boosting思想
1 AdaBoost算法
1)概念(关注提升过程)
算法在每一轮迭代过程中,会给每个样本赋予权重,预测越正确的样本降低其权重,反之提高权重
2)算法原理
第一点:将基分类器的线性组合作为强分类器,给分类误差小的基分类器以较大的权重,给分类误差大的基分类器以较小的权重
第二点:损失函数(总分类器角度的错误率)
第三点:第k-1轮总学习器,第k轮总学习器,m轮总学习器损失函数
- k-1轮学习器
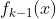
- k轮学习器
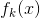
- m轮学习器损失函数
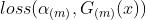
第四点:使m轮损失函数达到最小值时的
,是Adaboost的最终求解
- 每一轮G分类器在训练过程中,是使得误差率(基分类器角度)越小越好
- 每一轮中对损失函数
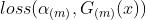 求
求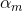 偏导
偏导
注意:求解![]() 偏导过程
偏导过程
![]()
![]()
![]()
3)算法流程
第一步:假定数据集
![]()
第二步:初始化训练集样本分布权重
第三步:使用具有权值分布
的训练集学习,得到基学习器
![]()
第四步:计算
在训练集上的分类误差
第五步:计算
的权重系数
(针对基分类器)
注意:误差![]() 越大,权重系数
越大,权重系数![]() 越小
越小
第六步:更新具有权值分布
的训练集(使用归一化因子
)
![]()
第七步:构建基本学习器的线性组合
第八步:最终分类器
注意:可以指定每个弱学习器的缩减系数![]()
![]()
4)算法优缺点
第一点:优点
- 可以处理连续值或者离散值的目标属性
- 可以将不同的分类算法作为弱学习器
- 解释性强,结构简单
第二点:缺点
- 对异常样本敏感,即异常样本在迭代过程中获得比较高的权值,影响模型的效果
- 迭代次数(弱分类器个数)不好确定
- 弱分类器之间存在关联,无法并行训练模型,只能串行训练模型
2 GBDT(Gradient Boosting Dicision Tree)
1)算法概念
算法在每一轮迭代过程中,使用残差更新目标属性,预测越正确的样本残差越小,反之越大
注意:GBDT由三部分构成,回归树、梯度提升、缩减系数
2)算法流程(以回归问题为例)
第一步:假定数据集
![]()
第二步:基学习器采用回归树,使用平方和损失或者绝对值损失函数(推荐平方和损失函数)
- 设定
 由一组基回归树
由一组基回归树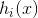 组成
组成
注意:为防止基回归树过拟合,添加缩放系数
- 平方和损失函数(推荐使用)
- 绝对值损失函数(不推荐使用)
- 最优解
![]()
第三步:初始化初始函数
(常数函数)
![]()
注意:实际算法中C一般按照均值方法初始化常数函数![]()
第四步:第m轮迭代中构建回归树
- 第m轮迭代中(考虑单个样本损失),使用梯度下降方法计算学习率(残差)
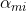
- 第m轮迭代中,使用数据集
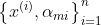 拟合CART回归树,得到第m棵树
拟合CART回归树,得到第m棵树
第一点:第m棵树第j个叶子节点的预测值![]()
第二点:样本在第m棵树的预测值![]()
- 第m轮迭代中,样本
 的预测值
的预测值
第五步:总模型
![]()
添加缩放系数![]() :
:
3)算法处理分类问题,损失函数采用对数损失函数(交叉熵损失函数)
第一点:二分类
- 损失函数
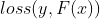
- 学习率
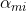
- 初始值
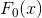
注意:表示总样本中正负样本的比率的对数
第二点:多分类(目标属性采用多标签)
- 损失函数:
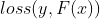
- 学习率
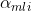
- 初始值
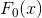
![]()
4)算法优缺点
第一点:优点
- 可以处理连续值和离散值的目标属性
- 在相对较少的调参情况下,模型效果也不错
第二点:缺点
- 弱分类器之间存在关联,无法并行训练模型,只能串行训练
3 XGBOOST(GBDT的变种算法)
1)算法概念
算法在每一轮迭代过程中,使用残差更新目标属性,预测越正确,残差越小,反之亦然
2)算法原理
第一点:损失函数 = GBDT损失函数 + 正则化项(L2正则)
![]()
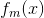 表示
表示 在第m棵树上的第
在第m棵树上的第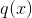 个节点预测值(
个节点预测值(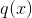 表示节点数)
表示节点数)
![]()
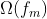 正则化项展开式(
正则化项展开式(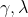 属于超参,
属于超参,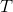 为m棵树上叶子节点个数)
为m棵树上叶子节点个数)
第二点:第m轮迭代后,损失函数
- 泰勒公式
- 损失函数
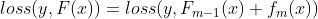 在
在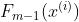 处展开二阶泰勒公式
处展开二阶泰勒公式
![]()
- 不考虑常数项的损失函数
- 定义第m棵树上的叶子节点
 上所有样本集合
上所有样本集合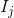
![]()
第三步:损失函数最小时的
![]()
![]()
![]()
第四步:将
带入损失函数
第五步:XGBoost损失函数
3)算法学习策略(树生成策略)
第一步:XGBoost算法原理所确定的损失函数,可以使得我们确定节点分裂的信息损失
第二步:选择特征属性以及分裂特征属性依据信息损失(不同于决策树的信息损失纯度度量)
- 对于任意叶子节点而言
第一点:分裂左节点(L)、右节点(R)之前的损失函数
第二点:分裂左节点(L)、右节点(R)之后的损失函数
- 叶子节点分裂前后信息损失
- 选择信息信息损失程度最大的方式进行叶子节点分裂
![]() 越大,分裂节点之后的信息损失越大
越大,分裂节点之后的信息损失越大
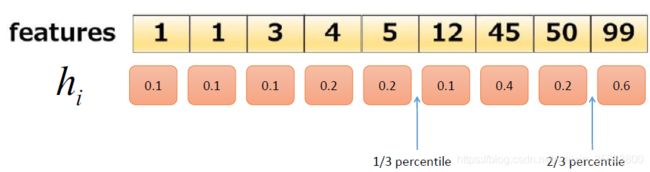
第三步:节点分裂是采用近似计算(分位数)
选择以及分裂特征属性,不是遍历每一个特征进行各种可能的分裂属性,而是依据二阶导数![]() 作为权重的分位数进行分裂属性
作为权重的分位数进行分裂属性
第一点:定义集合![]()
![]()
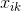 :表示第
:表示第 个样本第
个样本第 个特征属性值
个特征属性值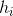 :表示第
:表示第 个样本损失函数的二阶导数
个样本损失函数的二阶导数
第二点:确定分位数位置
- 确定分位数集合
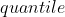 ,比如三分位数:
,比如三分位数: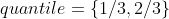
- 计算分位数位置
第三点:在第![]() 个特征的分位数位置进行分裂属性,计算信息损失程度大小
个特征的分位数位置进行分裂属性,计算信息损失程度大小
4)XGBoost特性(优点)
- 第一点:列采样方式,借鉴随机森林做法(即随机抽取k个特征构建树),有效降低过拟合
- 第二点:自动处理(填充)缺失值
- 第三点:并行计算,在特征粒度上计算Gain值采用并行计算,但是树的构建依然是串行,有效提升计算效率
- 第四点:正则项,降低模型复杂度,有效降低过拟合
- 第五点:基学习器不仅支持CART,也可以是线性回归,Logistic回归
- 第六点:支持自定义损失函数,但是要求二阶可导
四 Stacking思想
目前几乎不使用,深度学习神经网络比其更加具有优势


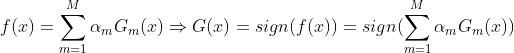
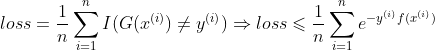
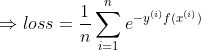

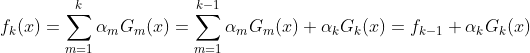
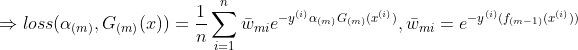
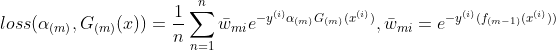
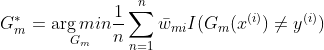
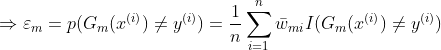
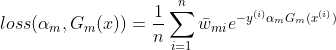

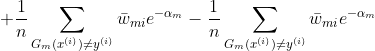
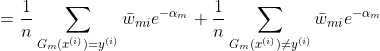
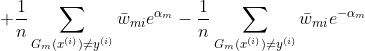



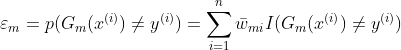

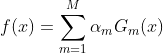

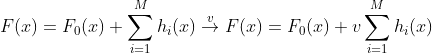



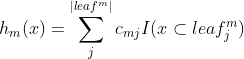
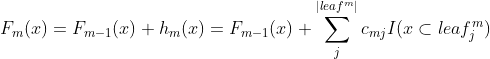
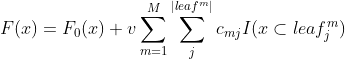
![loss(y,F(x))=-\sum_{i=1}^{n}[y^{(i)}logp(x^{(i)})+(1-y^{(i)})log(1-p(x^{(i)}))]](http://img.e-com-net.com/image/info8/c7fc387be087499f9a9c3ae1d1d90a38.gif)
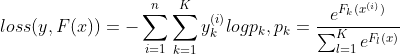
![\alpha _{mli}=-[\frac{\partial loss(y^{(i)}_{l},F_{l}(x^{(i)}))}{\partial F_{l}(x^{(i)})}|_{F_{l}(x^{(i)})=F_{m-1,l}(x^{(i)})}]=y^{(i)}_{l}-p_{m-1,l}(x^{(i)})](http://img.e-com-net.com/image/info8/f9c014925ee24fdc9343953f84dc2c03.gif)