编程之旅-Day21

目录

Day21-学习内容：

1.剑指Offer

面试题31：栈的压入、弹出序列

面试题33：二叉搜索树的后序遍历序列

 2.Leetcode

例1:字符串表示的数字乘法

例2:循转数组的搜索

 3.2018年校招编程题

例1:画家小Q

4.2017年阿里巴巴秋招笔试题

例22:问答题-淘宝邮费

5.阿里巴巴2017年实习生算法笔试题

6.专项训练-机器学习

---

1.剑指Offer

面试题31：栈的压入、弹出序列

题目描述：输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序，序列4,5,3,2,1是该压栈序列对应的一个弹出序列，但4,3,5,1,2就不可能是该压栈序列的弹出序列。（注意：这两个序列的长度是相等的）

思路：使用辅助栈

代码：

class Solution {
public:
    bool IsPopOrder(vector pushV,vector popV) {
        bool possible=false;
        if(!pushV.empty()&&!popV.empty()){
            int lenPush=pushV.size();
            int lenPop=popV.size();
            
            stack stack;
            int i,j;
            for(i=0,j=0;i

 

面试题33：二叉搜索树的后序遍历序列

题目描述：输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。

思路：后序遍历序列的最后一个结点是根结点，根结点之前的序列可分为两部分，第一部分是左子树序列，值都小于根结点的值，第二部分是右子树序列，值都大于根结点的值。整个过程递归实现。

代码：

class Solution {
public:
    bool VerifySquenceOfBST(vector sequence) {
        if(sequence.empty()||sequence.size()==0){
            return false;
        }
        int len=sequence.size();
        vector seqleft;
        vector seqright;
        
        int root=sequence[len-1];
        int i=0;
        for(;iroot){
                break;
            }    
            seqleft.push_back(sequence[i]);
        }
        int j=i;
        for(;j

 

 2.Leetcode

例1:字符串表示的数字乘法

题目描述：

Given two numbers represented as strings, return multiplication of the numbers as a string. 

Note: The numbers can be arbitrarily large and are non-negative. 

 

思路：将字符串从低到高的每一位转化成数字取出来分别相乘求和。

注意：字符转化为数字 int b=num2[j]-'0';
            数字转化为字符 result[i]=carry+'0';

代码：

class Solution {
public:
    string multiply(string num1, string num2) {
        int len1=num1.length();
        int len2=num2.length();
        int carry=0;
        string result(len1+len2,'0');
        for(int i=len1-1;i>=0;i--){
            int a=num1[i]-'0';
            for(int j=len2-1;j>=0;j--){
                int b=num2[j]-'0';
                int c=result[i+j+1]-'0';
                int v=a*b+c+carry;
                result[i+j+1]=v%10+'0';
                carry=v/10;
            }
            if(carry){
                result[i]=carry+'0';
                carry=0;
            }
        }
        int i=0;
        while(i

 

例2:循转数组的搜索

题目描述：

Suppose a sorted array is rotated at some pivot unknown to you beforehand. 

(i.e.,0 1 2 4 5 6 7might become4 5 6 7 0 1 2). 

You are given a target value to search. If found in the array return its index, otherwise return -1. 

You may assume no duplicate exists in the array.

思路：二分查找法，重点在于左右边界的确定。整个旋转数组分为两部分，一定有一部分有序，那么通过判断左边还是右边有序分为两种情况，然后再判断向左走还是向右走。

代码：

class Solution {
public:
    int search(int A[], int n, int target) {
        int first=0;
        int last=n-1;
        while(first<=last){
            int mid=first+(last-first)/2;
            if(A[mid]==target) return mid;
            if(A[first]<=A[mid]){   //左边有序
                if(A[first]<=target&&target

暴力法：

class Solution {
public:
    int search(int A[], int n, int target) {
        for(int i=0;i

 

 3.2018年校招编程题

例1:画家小Q

题目描述：

画家小Q又开始他的艺术创作。小Q拿出了一块有NxM像素格的画板, 画板初始状态是空白的,用'X'表示。
小Q有他独特的绘画技巧,每次小Q会选择一条斜线, 如果斜线的方向形如'/',即斜率为1,小Q会选择这条斜线中的一段格子,都涂画为蓝色,用'B'表示;如果对角线的方向形如'\',即斜率为-1,小Q会选择这条斜线中的一段格子,都涂画为黄色,用'Y'表示。
如果一个格子既被蓝色涂画过又被黄色涂画过,那么这个格子就会变成绿色,用'G'表示。
小Q已经有想画出的作品的样子, 请你帮他计算一下他最少需要多少次操作完成这幅画。

输入描述:

每个输入包含一个测试用例。
每个测试用例的第一行包含两个正整数N和M(1 <= N, M <= 50), 表示画板的长宽。
接下来的N行包含N个长度为M的字符串, 其中包含字符'B','Y','G','X',分别表示蓝色,黄色,绿色,空白。整个表示小Q要完成的作品。

输出描述:

输出一个正整数, 表示小Q最少需要多少次操作完成绘画。

输入例子1:

4 4
YXXB
XYGX
XBYY
BXXY

输出例子1:

3

例子说明1:

XXXX
XXXX
XXXX
XXXX
->
YXXX
XYXX
XXYX
XXXY
->
YXXB
XYBX
XBYX
BXXY
->
YXXB
XYGX
XBYY
BXXY

思路：直接遍历数组，遇到Y就朝右下角遍历，遇到B就朝左下角遍历，遇到G就朝两个方向遍历。

代码：

#include 
using namespace std;

char c[55][55];
int n,m;
void findY(int i ,int j){
    if(i>=0&&i=0&&j=0&&i=0&&j

 

4.2017年阿里巴巴秋招笔试题

例22:问答题-淘宝邮费

题目描述：淘宝上的每个宝贝一般都有个默认的全国邮费（也可能没有），同时也支持到特定省份有特定的邮费，如果到特定的省份没有特别的邮费就用默认的全国邮费。请： 

 1.设计一个存储结构来保存一个宝贝的所有邮费信息；（简单用文字阐述一下做法） 

 2.给定一个宝贝的邮费存储信息和一个省份，编程快速得出宝贝到此省的邮费。 注意：邮费的类型是uint32_t，此外由于商品数量非常大（假定十亿量级），查询量也非常大，对存储和查询的效率要求非常高，因此存储效率和查询效率是考察的重点。

代码：

//假设34个省的id为0--33
struct postage_info{
    uint64_t mask;//总共34各省，用34位表示每个省的邮费是不是默认，是的话对应位为1
    struct postage *p; //用一个数组存储非默认省份的价格，假设此数组按province_id的大小已经排好序了
    uint32_t default; //默认价格
}
struct postage{
  int province_id;  // 省id
  int postage;      //邮费
}
uint32_t get_postage(int province_id, struct postage_info * info){
       if(1<mask)
            return info->default;
       else
            return bsearch(province_id, info->p)//... 使用二分查找获取对应省份的邮费
}

 

5.阿里巴巴2017年实习生算法笔试题

例1:用十进制计算30!（30的阶乘），将结果转换成3进制进行表示的话，该进制下的结果末尾会有____个0。（E）正确答案: E   你的答案: C (错误)

A.6 B.8 C.10 D.12 E.14 F.16

解析：计算N！下三进制结果末尾有多少个0，其实就是计算三进制中的3被移位了多少次，就像二进制一样，每乘以2就向左移一位，末尾补0，因此这道题只要将N！因式分解成3^m*other，m就是答案。 

技巧性的解法就是m=N/3+N/(3^2)+N/(3^3)....+N(3^k) (k<=N/3)， 

用代码实现即为： 

sum=0; 

while(N){ 

    sum+=N/3;

    N=N/3;

} 

return sum;

 

例2:小赵和小钱二人分别从寝室和图书馆同时出发，相向而行。过了一段时间后二人在中途相遇，小赵继续向图书馆前进，此时：若小钱继续向寝室前进，则当小赵到达图书馆时，小钱离寝室还有600米；若小钱立即折返向图书馆前进，则当小赵到达图书馆是，小钱离图书馆还有150米。那么图书馆与寝室间的距离是____。 （F）正确答案: F   你的答案: E (错误)

A.1300m B.1250m C.800m D.1050m E.1100m F.900m

解析：

 

例3:某开发团队有6位开发同学,需参加5个项目， 每个项目都有人做 ,每位同学需要恰好参加1个项目,那么总共有____ 种不同的分配方案 （D）正确答案: D   你的答案: D (正确)

A.7200 B.3600 C.2700 D.1800 E.900 F.30

解析：C6 2 *A5 5

 

例4:下列选项中，识别模式与其他不一样的是___E_。

A.用户年龄分布判断：少年、青年、中年、老年

B.医生给病人诊断发病类型

C.投递员分拣信件

D.消费者类型判断：高消费、一般消息、低消费

E.出行方式判断：步行、骑车、坐车

F.商家对商品分级

解析：可以理解为，E中的类型划分标准是客观的，不需要不是主观界定的；而其余选项中的界定标准是主观设置的，不同的主管对象设置标准可能会出现不同，所以它们和E中的划分标准不同。分类和回归的区别。E是清晰的分类问题，其余选项是不清晰的，需要划分范围。 

 

例5:如下SQL语句中，_D___可能返回null值。 正确答案: D   你的答案: A (错误)

(1) select count(*) from t1; 

(2) select max(col1) from t1; 

(3) select concat('max=',max(col1)) from t1; 

A.(1)可能，(2)和(3)不可能

B.(2)可能，(1)和(3)不可能

C.(3)可能，(1)和(2)不可能

D.(1)不可能，(2)和(3)可能

E.都不可能

F.都可能

解析：

(1). 若表t1中有记录，会返回记录数；若无记录，则返回0； 

(2). 若表t1中存在列col为null, 则结果返回null; 

(3). 若表t1中存在列col为null, 则结果返回null;

MySQL concat函数使用方法：
    CONCAT(str1,str2,…)  

返回结果为连接参数产生的字符串。如有任何一个参数为NULL ，则返回值为 NULL。

 

6.专项训练-机器学习

例1:Nave Bayes是一种特殊的Bayes分类器,特征变量是X,类别标签是C,它的一个假定是:(C) 正确答案: C   你的答案: C (正确)

A.各类别的先验概率P(C)是相等的

B.以0为均值，sqr(2)/2为标准差的正态分布

C.特征变量X的各个维度是类别条件独立随机变量

D.P(X|C)是高斯分布

解析：此处为条件性独立，即已知类别的情况下各属性相互独立

 

例2:已知一组数据的协方差矩阵P,下面关于主分量说法错误的是(C)  正确答案: C   你的答案: B (错误)

A.主分量分析的最佳准则是对一组数据进行按一组正交基分解, 在只取相同数量分量的条件下,以均方误差计算截尾误差最小

B.在经主分量分解后,协方差矩阵成为对角矩阵

C.主分量分析就是K-L变换

D.主分量是通过求协方差矩阵的特征值得到

解析：K-L变换与PCA变换是不同的概念，PCA的变换矩阵是协方差矩阵，K-L变换的变换矩阵可以有很多种（二阶矩阵、协方差矩阵、总类内离散度矩阵等等）。当K-L变换矩阵为协方差矩阵时，等同于PCA。

主分量分析就是主成分分析。

 

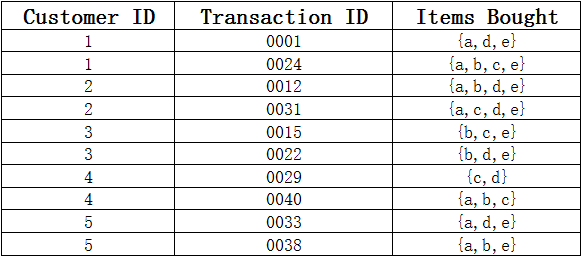
例3:考虑如下数据集，其中Customer ID(顾客id),Transaction ID(事务id),Items Bought(购买项)。如果将每个事务id看成一个购物篮，计算项集{e}, {b, d}, {b, d, e}的支持度:

• A.s({e}) =0.8s({b, d})= 0.2s({b, d, e})= 0.2

• B.s({e}) =0.7s({b, d})= 0.3s({b, d, e})= 0.3

• C.s({e}) =0.6s({b, d})= 0.4s({b, d, e})= 0.3

• D.s({e}) =0.8s({b, d})= 0.1s({b, d, e})= 0.1

解析：在关联规则度量中有两个重要的度量值：支持度和置信度 。对于关联规则R:A=>B，则： 
1. 支持度（suppport ）： 是交易集中同时包含A和B的交易数与所有交易数之比。 
Support(A=>B)=P(A∪B)=count(A∪B)/|D| 
2. 置信度（confidence ）： 是包含A和B交易数与包含A的交易数之比。 
Confidence(A=>B)=P(B|A)=support(A∪B)/support(A) 

 

例4:一般，k-NN最近邻方法在(B )的情况下效果较好 正确答案: B   你的答案: C (错误)

A.样本较多但典型性不好

B.样本较少但典型性好

C.样本呈团状分布

D.样本呈链状分布

解析：样本呈团状颇有迷惑性，这里应该指的是整个样本都是呈团状分布，这样kNN就发挥不出其求近邻的优势了，整体样本应该具有典型性好，样本较少，比较适宜。

样本数少：kNN每次预测要计算距离，所以是带着整个样本集跑的（也有些剪辑近邻之类的会剪掉一些），所以样本数越少越好。 

典型性：不仅是kNN，每个分类算法都希望样本典型性好，这样才好做分类。

 

例5:统计模式分类问题中，当先验概率未知时，可以使用(A、D) 正确答案: A D   你的答案: D (错误)

A.最小最大损失准则 B.最小误判概率准则 C.最小损失准则 D.N-P判决

解析：

A. 考虑p(wi)变化的条件下，是风险最小 

B. 最小误判概率准则， 就是判断p(w1|x)和p(w2|x)哪个大，x为特征向量，w1和w2为两分类，根据贝叶斯公式，需要用到先验知识 

C. 最小损失准则，在B的基础之上，还要求出p(w1|x)和p(w2|x)的期望损失，因为B需要先验概率，所以C也需要先验概率

D. N-P判决，即限定一类错误率条件下使另一类错误率为最小的两类别决策，即在一类错误率固定的条件下，求另一类错误率的极小值的问题，直接计算p(x|w1)和p(x|w2)的比值，不需要用到贝叶斯公式。