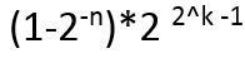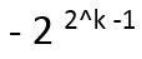华中科技大学计算机组成原理慕课答案-第二章-数据表示

单选

1　计算机中表示地址时使用
√A. 无符号数
B. 反码
C. 原码
D. 补码

2　浮点数的表示范围和表示精确度分别取决于
A. 阶码的编码和尾数的编码
√B. 阶码的位数和尾数的位数
C. 机器字长和阶码的位数
D. 尾数的位数和阶码的位数

3　设G(x) = 1011，某(7,4)码为K1K2K3K4K5K6K7，仅K7出错时进行CRC校验得到的余数为001，当仅K5出错时，进行CRC校验得到的余数为
√A. 100
B. 011
C. 010
D. 110

根据CRC校验的余数的循环，将K7出错时的得到的余数后面加一个0，再用生成多项式1011做模2的除法可以得到K6出错时的余数。
0010/1011……010 在得到的余数后面加一个0，再用生成多项式1011做模2的除法就可以得到K5出错时的余数 100/1011……100
答案为100
参考：https://blog.csdn.net/qq_20115319/article/details/107310235

4　如果某系统15*4=112成立，则系统采用的进制是
√A. 6
B. 9
C. 8
D. 7

设使用的是p进制，则15*4=112等价于：
(p + 5) * 4 = p^2 + p + 2
解出来p=-3（舍去）和p=6
参考：https://blog.csdn.net/xhyxxx/article/details/64132917

5　2^100 mod 7 =
A. 5
√B. 2
C. 4
D. 3

2＾3=8 mode 7 =1，
100 mod 3=1,
2＾100=2＊2＾99 mod 7=2.

6　字长5位的待编码二进制有效数据为11011，对它进行CRC编码时采用的生成多项式代码为1011，则得到的CRC编码为
A. 11011010
B. 11011101
C. 11011100
√D. 11011001

11011000模2除以1011得余数001。
1101/1011=0110，左移一位
1101/1011=0110，左移一位
1100/1011=0111，左移一位
1110/1011=0101，左移一位
1010/1011=0001。余数位数少于除数，为最终余数。

7　某十六进制浮点数A3D00000中最高8位是阶码（含1位阶符），尾数是最低24位（含1位数符），若阶码和尾数均采用补码，则该浮点数的十进制真值是
A. -0.375×2^(-35)
B. -0.625×2^(-93)
√C. -0.375×2^(-93)
D. 0.625×2^(-35)

要注意此处不是IEEE754，不用-127也不用加上尾数中最高位的1
A3D00000=1010 0011 1101 0000 0000 0000 0000 0000
转换成原码1101 1101 1011 0000 0000 0000 0000 0000
101 1101=93，011=0.25+0.125=0.375。符号位都是负。
答案：(-1)＊2＾(-93) ＊(-0.375)
参考：https://blog.csdn.net/qq_20115319/article/details/107310235

8　存储器中地址号分别为1000#、1001#、1002#、1003的4个连续存储单元，分别保存的字节数据是1A、2B、3C、4D，如果数据字长为32位,存储器采用的是小端对齐模式，则这4个存储单元存储的数据值应被解析为
√A. 4D3C2B1A
B. D4C3B2A1
C. 1A2B2C3D
D. A1B2C3D4

9　字长8位的某二进制补码整数为11011010，则该数的标准移码是
A. 00111010
B. 11011010
C. 10111010
√D. 01011010

移码用于表示浮点数的阶码，整数表示。移码和补码的关系为：n位整数补码的符号位取反即可得相应的移码。有关原理，我做了一个示意图如下：

10　两个字长16位的补码0A2B和E16A, 带符号扩展成32位后的结果分别
A. 00000A2B和0000E16A
√B. 00000A2B和FFFFE16A
C. FFFF0A2B和0000E16A
D. 11110A2B和FFFFE16A

11　对于IEEE754格式的浮点数，下列描述正确的是
A. 阶码用移码表示，尾数用补码表示
√B. 阶码用移码表示，尾数用原码表示
C. 阶码和尾数都用原码表示
D. 阶码和尾数都用补码表示

阶码用移码表示，尾数用原码表示。
补充：单精度浮点数字长32位，符号位S占1位，指数E占8位，尾数M占23位，指数偏移量127，用移码表示；双精度浮点数字长64位，符号位S占1位，指数E占11位，尾数M占52位，指数偏移量1023，用移码表示；
约定M的小数点左边隐含一位1，完整的尾数形式为1.M，但在进行浮点数据表示时只保存M。所以上述单精度尾数长度实际为24，双精度尾数长度实际为53，这也是偏移量不是128或1024的原因；

12　对字长为8位的二进制代码10001101，下列说法错误的是
A. 如果代码为无符号数，则其十进制真值为+141
√B. 如果代码为标准移码数，则其十进制真值为+115
C. 如果代码为原码数，则其十进制真值为-13
D. 如果代码为补码数，则其十进制真值为-115

B. +13。

13　下列对海明校验的描述中，正确的描述是
√A. 待编码数据长度为4位，再增加3位校验码就可以检测到仅1位数据出错的情况并纠错
B. 海明校验码的码距与校验位的位数没有关系
C. 分成r组时，可以得到r位指误码，因此可以区分2＾r种只有1位出错的情况
D. 在任何条件下，海明校验都无法检测到多位数据同时出错的情况

B. 一般情况，增加校验的同时也增大了码距。
C. 要去掉校验码占的位。分成r组时，可以得到r位指误码，因此可以区分(2＾r-r)种只有1位出错的情况。
D. 将有效信息按某种规律分成若干组，每组安排一个校验位，做奇偶测试，就能提供多位检错信息，以指出最大可能是哪位出错，从而将其纠正。实质上，海明校验是一种多重校验。

14　若浮点数的尾数是用5位补码来表示(其中符号位1位)，则下列尾数中规格化的尾数是
√A. 10000和01001
B. 01011和11010
C. 01100和11110
D. 11011和01011

A. 原码：1.0000, 0.1001，都是规格化的。

15　下列关于补码和移码关系的描述中，错误的是
A. 相同位数的补码和移码具有相同的数据表示范围
B. 一般用译码表示浮点数的阶码，而用补码表示定点数
C. 同一个数的补码和移码，其数值部分相同，而符号相反
√D. 零的补码和移码相同

D. 不同，零的移码是1.0000，符号位也要变反。

多选

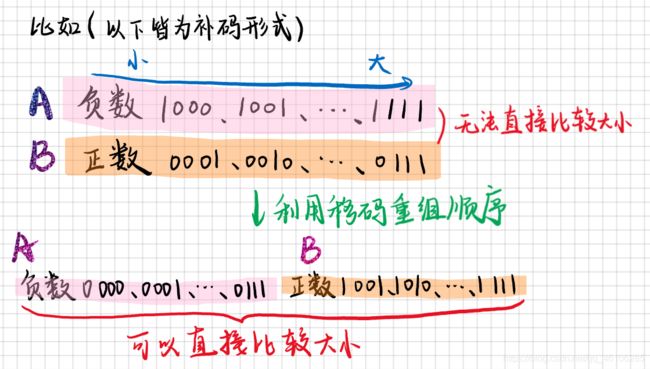
1　已知 定点小数[X]补 = 1.X1X2X3, 若要求X≤-0.75，则下列满足要求的是
√A. X1X2X3 = 000
√B. X1X2X3 = 001
C. X1X2X3 =101
√D. X1X2X3=010

转化成小数就可以了。

2　设规格化浮点数的阶码为k+1位(包含1位符号位)、尾数为n +1位(包含一位符号位)，若阶码和尾数均采用补码数据表示，下列关于该浮点数表示范围的描述中，正确的是
√A. 能表示的最小正数为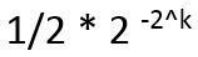

√B. 能表示的最大负数为

√C. 能表示的最大正数为

√D. 能表示的最小负数为

3　在IEEE 754浮点机器数中不出现的是
√A. 尾数中最高位的1
B. 尾数的符号位
C. 阶码的符号位
√D. 基数

C. 移码也是有符号位的。

4　关于奇偶校验的下列描述中，错误的是
A. 只需要1位校验位
B. 检测得到的有错结论可靠
√C. 可纠正1位错误
√D. 检测得到的无错结论可靠

5　计算机字长16位，采用补码表示整数，下列关于其表示数据范围的描述中正确的是
√A. 能表示的最小正数是1
√B. 能表示的最大负数是-1
√C. 能表示最大正数是(2^15) - 1
√D. 能表示的最小负数是- (2 ^15)

填空

1　十进制数5对应的32位IEEE754 格式的机器数为 （40A00000）H (采用十六进制表示,填写答案时不需要写最后的H)

2　某纠错码的全部码字为0000000000，0000011111,1111100000,1111111111。该编码的码距为（5）

3　字长5位的待编码二进制有效数据为10011，对它进行CRC编码时采用的生成多项式代码为1011，则得到的编码结果为（10011100）（填写二进制形式）

4　将一个十进制数-129表示成补码时，至少应采用多少位二进制数（9）

待补充。