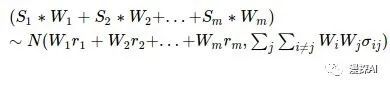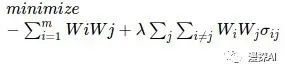【001】机器学习基础-凸优化基础

为什么开篇第一件事是介绍凸优化呢，原因很简单，就是它很重要！

凸优化属于数学最优化的一个子领域，所以其理论本身也是科研领域一门比较复杂高深的研究方向，常被应用于运筹学、管理科学、运营管理、工业工程、系统工程、信号处理、统计学等，我们主要关注其在机器学习中的应用。

---

类比于计算机程序由数据结构和算法组成一样，任何的AI问题可归结于以下公式：

模型：目标函数，旨为实现目标的途径，方法有神经网络、SVM、逻辑回归等
优化：本质为机器学习中的训练，为了更准确的接近目标得到最优的解，优化方法有SGD、AdaGrad、Adam、EM等

模型（目标函数）好建，优化才是机器学习的核心，而任何一个优化问题可以写成如下的一个标准形式：

min f (x)
s.t. : gi (x) ≤ 0, i = {1,.....,m}
hj (x) = 0, j = {1,.....,t}

常见的优化问题有：

1. 线性回归（Linear Regression）
2. 逻辑回归（Logistic Regression）
3. SVM（Support Vector Machine）
4. 协同过滤（Collaborative Filtering）
5. K均值（K-means）

当我们拿到一个AI问题时，在用上述的标准化形式确定目标函数之后，首先要做的就是判断目标函数的类型，确定其优化的方向。我们通常会通过以下４个维度来考量其类别：

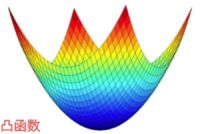
1. 凸函数　Or　非凸函数

如果目标函数是一个凸函数，就意味着这个函数有一个全局最优解（也就是极值点），可以直接通过算法确定出来，凸函数的局部最优解就是其全局最优解是凸优化最大的一个优势，非常经典的逻辑回归就是一个凸优化问题，而神经网络则是比较复杂的非凸优化问题。对于非凸函数，它存在很多的局部最优解，导致我们就很难在局部最优解中找到全局最优解，所以在这种优化问题中，我们的目标只是寻找到更好的局部最优解。

我们在解决问题时，希望尽量构造出来的目标函数是凸函数。对于部分的非凸函数，可以尽量通过一些变换转化凸函数，最后对得到的解做一些优化来得到更好的局部最优解。至于更加复杂的非凸函数优化问题，可采用预训练（可在优化前得到较理想的初始化位置）、选择合适的优化器来得到更好的结果。

2. 连续函数　Or　非连续函数

大部分的机器学习模型都是连续函数，只有少部分是非连续函数，而且这部分问题优化起来比较难，有兴趣可自行探索。

3. 带条件　Or　不带条件

不带条件的目标函数优化起来比较简单；带条件的略复杂一些，经常可以通过拉格朗日的方法可以把条件放到目标函数中一起优化。

4. 平滑　Or　不平滑

大部分的机器学习模型都是平滑的函数，在做梯度下降优化时，函数中的每个点都有梯度。而对于不平滑的函数，比如说L1正则就有一个顶点，在顶点处是没有梯度的，对于这种问题，通常会采用次梯度（subGradient）的方法来处理。

在以上４种类型中，判断目标函数是否为凸函数是最重要的。本章节我们先来介绍凸函数优化问题。

要理解凸优化，首先要知道两个概念：凸集、凸函数

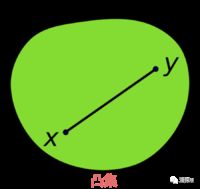
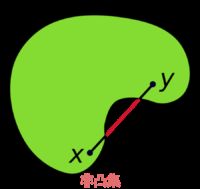
凸集（Convex Set）的定义：

假设对于任意的x,y∈C，并且任意参数α∈[0,1]，我们有αx + (1 - α)y∈C，则集合为凸集。简单来说，凸集就是过集合内C内任意两点之间的线段均在集合C内。

例子：

1. 所有的Rn
2. 所有的正数集合Rn+
3. 范数||x|| ≤ 1
4. 线性方程组式的所有解: Ax = b
5. 不等式的所有解: Ax ≤ b
6. 两个凸集的交集

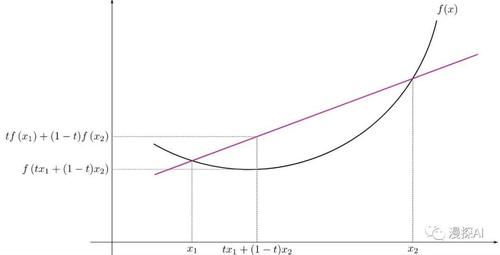
凸函数（Convex Function）的定义:

函数的定义域D(f)为凸集，对于定义域里任意x,y，且0 ≤θ ≤ 1函数满足

f (tx1 + (1-t)x2) ≤ tf (x1) + (1-t)f (x2)

例子：

1. 线性函数：f (x) = bTx + c
2. 二次函数：f (x) = xTAx + bTx + c（A为半正定矩阵）
3. exp x, -logx, xlogx
4. 范数函数

那么如何来判断凸函数呢？首先其定义域必须是凸集，值域可以用以下方法判断：

1. 对于一元函数f(x)，我们可以通过其二阶导数f″(x) 的符号来判断。如果函数的二阶导数总是非负，即f″(x) ≥ 0 ，则f(x)是凸函数
2. 对于多元函数f(X)，我们可以通过其Hessian矩阵（Hessian矩阵是由多元函数的二阶导数组成的方阵）的正定性来判断。如果Hessian矩阵是半正定矩阵，则f(X)是凸函数

凸优化(Convex Optimization)

凸优化就是对凸函数的优化，凸优化必须要满足三个条件：

1. 目标函数的最终要求是最小化（最大化问题取负可转化为最小化）
2. 目标函数是一个凸函数（凹函数取负可转化为凸函数）
3. 约束条件所形成的可行域集合是一个凸集

凸函数优化主要以下几点优势：

1. 凸优化问题的局部最优解就是全局最优解，这一点尤为重要，因为在优化领域最头疼的就是局部最优解没办法保证解的质量，而凸函数就不存在这个问题。
2. 虽然实际中由于噪声或者各种约束条件的存在，大部分的问题都是非凸的，但是很多非凸问题都可以被等价转化为凸优化问题或者被近似为凸优化问题（例如拉格朗日对偶问题）。
3. 当一个问题被归为一个凸优化问题时，基本可以确定该问题是可被求解的。

在实际解决实际优化问题时，可按照以下思路进行：

1. 确定参数、变量
2. 确定目标函数
3. 约束条件（s.t.）
4. 判断目标函数类型
5. 设计解决方案

下面来看两个经典的凸优化问题

１．交通问题

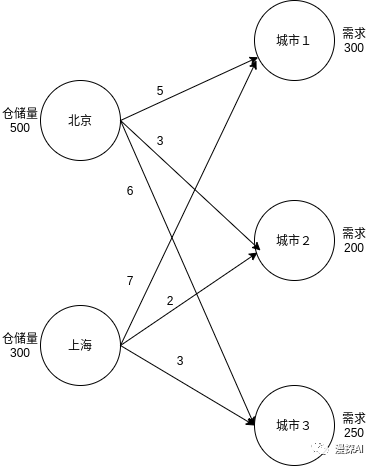
问题描述：如下图所示，假设有北京和上海两个衣服仓库，分别存有500、300件衣服，现要从两个仓库中把衣服分别运往三个城市，三个城市的需求分别为300、200、250件，北京运输到三个城市的代价分别为5、3、6，上海运输到三个城市的代价分别为7、2、3。求解最合适的运输方案，使得运输代价最小。

image

接下来按照解题思路，求解该问题

1. 确定参数、变量

设从北京发往三个城市的衣服数量分别为B1，B2，B3；从上海发往三个城市的衣服数量分别为S1，S2，S3

2. 确定目标函数

minimize 5B1+ 3B2 + 6B3 + 7S1 + 2S2 + 3S3

3. 约束条件（s.t.）

B1 +S1 = 300
B2+S2 = 200
B3+S3 = 250
B1 +B2 +B3 ≤ 500
S1+S2 +S3≤ 300
B1,B2,B3 ,S1,S2,S3 ≥ ０

4. 判断目标函数类型

目标函数和条件均为线性函数，该问题为典型的线性规划问题(Linear Programming)

5. 设计解决方案

明确了目标函数、约束条件、函数类型之后，就可以对该函数进行优化。该问题为经典的线性规划问题，有很多现成的优化方案，这里就不在赘述，例如可参考cvxopt的Linear Programming( http://cvxopt.org/userguide/coneprog.html#linear-programming )，我们只需要将条件转换为对应向量，作为输入就好。

２．投资组合问题

问题描述：将一笔钱分别投资到m支股票中，如何分配可得到最大化收益( 假设每只股票的收益服从正太分布N(ri, ði2))

接下来按照解题思路，求解该问题

1. 确定参数、变量

股票：1,2,3,4,5,......,m
第 i 只股票的配置权重（百分比）：Ｗi
第 i 只股票的收益：Si ~ N(ri, ði2)
则最后的投资组合为：

其中上式中，均值为该投资组合的收益，方差为风险

2. 确定目标函数

目的：最大化收益 ＋ 最小化风险
则目标函数为：

其中λ为超参数，代表风险偏好

3. 约束条件（s.t.）

所有股票配置的权重加起来等于1，也就是：

4. 判断目标函数类型

目标为二次方，条件为线性，该函数为凸二次规划（Convex Quadratic Programming）问题。

5. 设计解决方案

可以参考cvxopt的Quadratic Programming( http://cvxopt.org/userguide/coneprog.html#quadratic-programming )比较标准式。

注：这里只构造了基础的投资模型，切不可按此投资股票，因为在实际投资中，要考虑更多的问题，比如：基本面风险、消息面风险、股票成本等等（更何况大A股呢）。