图神经网络(GCN)中的过度平滑(over-smooth)问题以及 multi-hops解决思路
0. 图神经网络(GCN)中的过度平滑(over-smooth)问题
什么叫做图神经网络的过渡平滑问题?即在图神经网络的训练过程中,随着网络层数的增加和迭代次数的增加,每个节点的隐层表征会趋向于收敛到同一个值(即空间上的同一个位置)。
不是每个节点的表征都趋向于收敛到同一个值,更准确的说,是同一连通分量内的节点的表征会趋向于收敛到同一个值。这对表征图中不通簇的特征、表征图的特征都有好处。但是,有很多任务的图是连通图,只有一个连通分量,或较少的连通分量,这就导致了节点的表征会趋向于收敛到一个值或几个值的问题。
所以over-smooth的现象就是多次卷积后,同一连通分量内所有节点的特征都趋于一致了。
那么我们是否需要解决over-smooth问题呢?
首先我们要观察数据集中的那些节点,是不是本身语义信息就非常的一致。如果本身语义信息就非常一致,那么我们就不需要解决过渡平滑问题问题,但是!!!如果我们在GCN中连通图中的节点个性化信息非常丰富,那么我们明显是不希望出现过度平滑的。
1. 如何解决over-smooth 的问题
图卷积会使同一连通分量内的节点的表征趋向于收敛到同一个值。
- 针对“图卷积”:在当前任务上,是否能够使用 RNN + RandomWalk(数据为图结构,边已然存在)或是否能够使用 Attention(数据为流形结构,边不存在,但含有隐式的相关关系)?
- 针对“同一连通分量内的节点”:在当前任务上,是否可以对图进行 cut 等预处理?如果可以,将图分为越多的连通分量,over-smooth 就会越不明显。
我们刚才说是由于多次卷积而导致的过度平滑问题,即深度上的拓展所导致的问题。随着图卷积渗透到各个领域,一些研究开始放弃深度上的拓展,选择效仿 Inception 的思路拓宽网络的宽度,通过不同尺度感受野的组合对提高模型对节点的表征能力。下面将结合最新论文来讲述。
2. DIRECT MULTI-HOP ATTENTION BASED GRAPH NEURAL NETWORKS
2.1 摘要
目前GNNs通过利用self-attention机制已经取得较好的效果。但目前的注意力机制都只是考虑到相连的节点,却不能利用到能提供图结构上下文信息的多跳邻居(multi-hop neighbors)。因此提出 Direct multi-hop Attention based Graph neural Network (DAGN),在注意力机制中加入多跳信息,从邻居节点扩展到非邻居节点,增加每一层网络中的感受野(receptive field)。同时,DAGCN采用diffusion prior的方法来计算节点对上的attention values。实验结果表明能取得 state-of-the-art 的结果。
2.2 动机
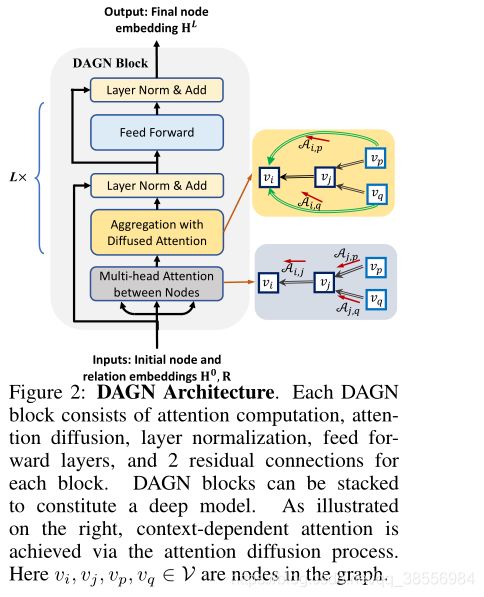
目前GNNs中的attention仅局限于直接邻居,因此每一层的感受野局限在one-hop结构中。直接stack更多的GAT层会带来 oversmoothing problem。此外,edge attention values也只与节点表示本身有关,没有考虑到图结构的上下文信息。将多跳邻居上下文信息考虑到GNNs的注意力计算还没有被研究。本文提出了DAGN模型具有新颖的 graph attention diffusion layer,如图一所示,其主要有两个优势:
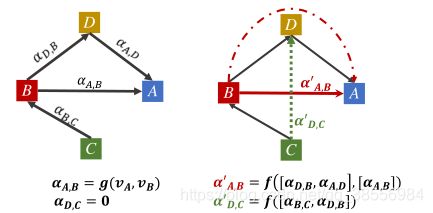
①DAGN在每个消息传递层捕获多跳之外的节点之间的远程交互。因此,该模型能够实现有效的远程消息传递,从重要节点到多跳。
②DAGN的注意力计算依赖于上下文。以前的的注意值只取决于连接节点之间上一层的节点表示,相比之下,对于所选多跳邻域内的任何一对可达节点,DAGN通过聚集该对节点之间所有可能路径(长度≥ 1)上的注意力得分来计算注意力。
2.3 贡献
理论上,我们证明了DAGN基于图表结构将个性化页面排名(PPR)置于关注值之前。我们还利用谱图分析表明,DAGN具有强调大尺度图结构和降低图中高频噪声的能力。具体而言,DAGN放大对应于图中大规模结构的较低拉普拉斯特征值,并抑制对应于图中更多噪声和细粒度信息的较高拉普拉斯特征值。
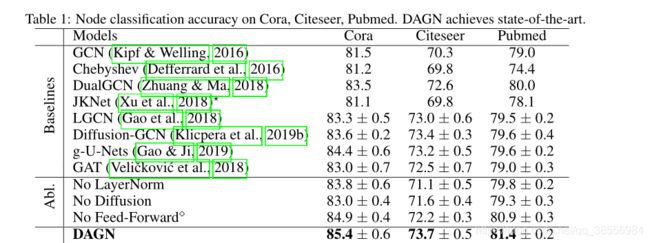
实验表明,DAGN实现了最先进的结果:DAGN实现了高达5.7%的相对误差减少了前最先进的科拉,赛和公共医疗。DAGN还在大规模开放图形基准数据集上获得了更好的性能。知识图完成后,DAGN在WN18RR和FB15k-237上的四个指标上取得了最先进的进展,命中指标的最大增益为7.1%。
此外,我们的消融研究揭示了DAGN基本组件的协同效应,包括层归一化和多跳扩散注意。我们表明,DAGN受益于模型深度的增加,而基线的性能在更小的模型深度处停滞不前。我们进一步观察到,与GAT相比,DAGN学习到的注意值具有更高的多样性,表明能够更好地关注重要节点。
2.4 基于有向多跳注意力的图形神经网络
2.4.1 多跳注意力扩散
我们首先引入注意力扩散,它对DAGN在每一层的注意力分数起作用。注意力扩散算子的输入是一组三元组 ( v i , r k , v j ) (v_i,r_k,v_j) (vi,rk,vj)。DAGN首先计算所有边缘的注意力得分。注意力扩散模块然后通过扩散过程,基于边缘注意力得分,计算没有被边缘直接连接的节点对之间的注意力的值。
Attention diffusion是每一层中用于计算DAGN‘s的attention分数。首先计算每一条边上的attention分数:
![]()
将上式应用到graph中的每一条边后,得到 attention score matrix :
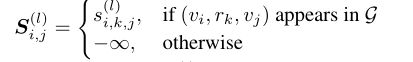
随后,通过对得score matrix 进行softmax得到 attention matrix :
![]()
在第二阶段,在网络中将不直接连接的节点之间启用注意力。该过程基于1-hop注意力矩阵的幂,通过图扩散来计算multi-hop邻居的注意分数:
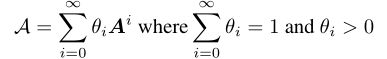
因此,本文定义了基于特征聚合的graph attention diffusion:
![]()
2.4.1 基于直接多跳注意力的GNN架构
上图提供了可多次堆叠的DAGN区块的架构概述。多头图注意力扩散层。多头注意用于允许模型在不同的视点联合关注来自不同表示子空间的信息。
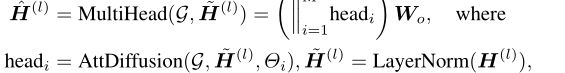
此外,我们的DAGN模块包含一个完全连接的前馈子层,由两层前馈网络组成。我们还添加了层归一化和残差两个子层中的连接,为每个块提供更具表现力的聚合步骤:
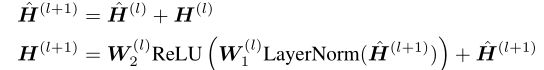
其实DAGN可以看作是GAT的扩展,加入了额外推导出的参数矩阵多条注意力矩阵,layer normalization和residual connection。
2.5 实验
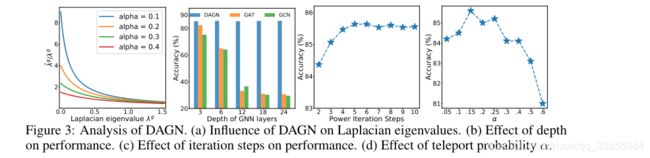
当考虑多跳邻居信息(K > 1)时,我们观察到性能显著提高。然而,对于K ≥ 6,增加迭代步数K具有递减的收益。此外,我们发现最佳K与最大节点平均最短路径距离相关,这为选择最佳k提供了指导。我们还观察到,对于大于0.25的α,精度显著下降。这是因为小α增加了低通效应(图3 (a))。然而,α太小导致模型只关注大规模的图结构,而忽略了太多的高频信息。
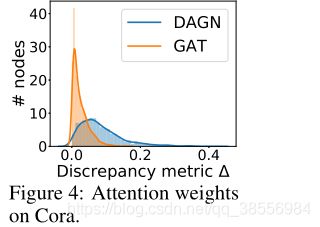
相对于GAT,DAGN的Attention Distribution分布有larger discrepancy,说明更能分辨出重要的节点。