混杂因素通常具备以下几个特点:
*混杂因素必须与研究结局密切相关;
* 混杂因素又与研究的暴露/处理因素有关;
* 混杂因素一定不是暴露/处理因素和研究结局之间因果。
残余混杂(Residual Confounding):未知且无法测量的混杂因素对结果造成的偏倚。
常用控制混杂的方法:(观察性研究)
*分层分析
*多因素分析(线性回归/logistic回归/cox回归 )
*倾向性评分分析
*工具变量分析
1.分层分析
它是将数据资料按照某个需要控制的混杂因素进行分层,然后再估计暴露/处理因素与研究结局之间的关联性。
分层分析的一般步骤:
*计算总人群中暴露/处理因素与研究结局的效应值,即粗RR(相对危险度)或OR(比值比)值;
*将研究资料按照混杂因素来进行分层,计算各层内暴露/处理因素与研究结局的效应值,即分层RR或OR值;
*判断各层之间的效应值是否一致,即判断层间RR或OR值是否相近或同质。若各层之间的RR或OR值不一致,则不能 合并,需要分层报告效应值。
若各层之间的RR或OR值基本一致,则可以用M-H(Mantel-Haenszel)法计算合并的效应值,即调整(控制混杂因素后)的RR或OR值;再将合并的RR或OR值与分层前的粗RR或OR值进行比较。
若调整后的RR或OR值与粗RR或OR值不一致,可以认为分层因素存在混杂作用【《流行病学(第六版)》建议,差值在0.1以上(RR或OR<1时),或在0.5以上(RR或OR>1时)时,认为调整后RR或OR值与粗RR或OR值不一致】。此时,还要结合临床或生物学意义进行综合分析,而不应该仅仅根据统计学结果来判断。
分层分析仅仅适用于混杂因素较少,且多为分类变量的情况,最简单。
2.多因素(调整)分析法
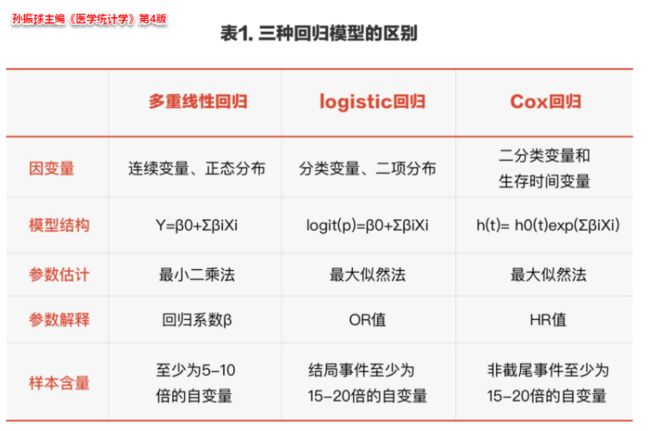
它是把多个变量之间的内在联系和相互影响考虑在内,同时分析多个因素对结局的影响。构建一个多因素调整的回归方程,其中方程的因变量为结局事件,而自变量包括暴露/处理因素(如药物、手术等)及混杂因素(如年龄、性别、疾病严重程度等)。三种回归模型即:多重线性回归、logistic回归及Cox回归
构建回归方程
*因变量:结局事件;
*自变量:暴露/处理因素+混杂因素
研究者需要关注的3个问题:(JAMA期刊发表的一篇文章《Adjusted Analyses in Studies Addressing Therapy and Harm》总结)
1. Did the investigator identify all known prognostic factors for the outcome of interest?(研究人员是否已经识别出 所有与结局事件相关的预后因素?)
为了减少残余的混杂偏倚,我们需要尽可能识别更多的混杂因素,保证信息的全面性。
2. Did the investigator accurately measure all these prognostic factors?(这些预后因素是否被准确地测量?)
为了保证测量的准确性,应尽可能使用客观指标,减少主观判断,提高检测的灵敏度。
3. Did the investigator conduct an adjusted analysis that included all these prognostic factors?(在多因素调整分 析 中,是否校正了所有已知的预后因素?)
控制混杂因素的个数主要取决于发生结局事件的多少。控制的混杂因素越多,所需要的结局事件的例数就越多。
注意:但是由于研究者往往无法全面收集信息,或者无法进行准确测量,或者仍存在一些未知的混杂因素,而回归模型中需要调整的混杂因素的个数又往往受到结局事件的限制,这些都会对多因素回归模型的结果造成一定的偏倚,在应用时也需要多加注意。
分层分析法和多因素调整分析法共同的局限性:同时调整的混杂因素的数量不能太多,且受到结局事件例数的限制。
三种回归模型的选择:
3.倾向性分析(Propensity Analysis)
倾向性评分是指在一定协变量条件下,一个观察对象接受某种暴露/处理因素的可能性,它是一个从0到1的范围内连续分布的概率值。
其基本原理是将多个混杂因素的影响用一个综合的倾向性评分来表示,从而降低了协变量的纬度,减少了自变量的个数,有效的克服了分层分析和多因素调整分析中要求自变量个数不能太多的短板。
那么在进行倾向性分析之前,第一步就是要计算出每个研究对象的倾向性评分。倾向性评分的估计是以暴露/处理因素作为因变量Y(0或1),其他混杂因素作为自变量X,通过建立一个回归模型来估计每个研究对象接受暴露/处理因素的可能性,最为常用的是logistic回归模型。
用logistic回归模型估计倾向性评分,操作简单容易实现,可以直接得到倾向性评分分值,结果也易于理解。倾向性评分越接近于1,说明患者接受某种暴露/处理因素的可能性更高,越接近于0,说明患者不接受任何暴露/处理因素的可能性更大。
(1)倾向性评分匹配法
倾向性评分是一个能够反映多个混杂因素影响的综合评分,我们可以将两组人群按照倾向性评分从小到大来进行匹配,仅用匹配倾向性评分一个指标来达到同时控制多个混杂因素的目的。倾向性评分匹配是倾向性分析中应用最为广泛的一种方法。
首先我们要计算出每一个研究对象的倾向性评分,然后从小到大进行排序,对于每一个暴露/处理组的研究对象,从对照组中选取与其倾向性评分最为接近的所有个体,并从中随机抽取一个或N个研究对象作为匹配对象,直至所有的研究对象均匹配完毕,未匹配上的研究对象则进行舍去。
(2)倾向性评分分层法
在第一期的内容中我们介绍了传统的分层分析法,是利用原始的混杂因素来进行分层,当有K个混杂因素时,就需要将样本一共分为2k个层,混杂因素较多时,就有可能出现某些层里只有几个同时满足分层条件的研究对象,甚至是没有满足条件的研究对象,在这种情况下传统的分层分析计算较为复杂,且结果也会产生一定的偏倚。
现在我们可以通过构建回归模型,利用K个混杂因素计算出倾向性评分值,仅用倾向性评分一个变量来进行分层,避免产生分层过多的问题,同时每个层里的研究对象也具有较高的同质性。通常情况下,我们可以按照倾向性评分的大小,将研究对象分为5-10层,在每一层混杂因素达到均衡的状态下,分析暴露/处理因素X与因变量Y之间的关系。
(3)倾向性评分校正法
倾向性评分校正的方法是将倾向性评分和传统的回归分析相结合的一种方法。我们在介绍多因素调整的方法中提到,其控制混杂因素的个数主要取决于发生结局事件的多少,控制的混杂因素越多,所需要的结局事件的例数就越多。因此对于一些罕见病的研究,或是当收集到的结局事件很少时,如果采用多因素调整的方法,就很难全面控制多个混杂因素。
倾向性评分的一个优势就在于,它可以将多个混杂因素的影响用一个综合的倾向性评分来表示,从而减少了自变量的个数。在构建回归模型时,只需要将倾向性评分作为一个协变量,然后再将暴露/处理因素作为分析变量纳入到回归模型中,以此分析在控制倾向性评分后,暴露/处理因素与结局变量之间的关联性,因此通过控制倾向性评分一个变量,就达到了控制多个混杂因素的作用。
(4)倾向性评分加权法
倾向性评分加权法的原理与传统的标准化法的原理类似。标准化法的基本思想是制定一个统一的“标准人口”,按照“标准人口”中混杂因素构成的权重来调整两组观察效应的平均水平,从而消除两组之间由于内部混杂因素分布不同对效应值的影响。
倾向性评分加权法在计算得出倾向性评分的基础上,利用标准化法的原理,通过倾向性评分值赋予每个研究对象一个相应的权重进行加权,使得各组中倾向性评分分布一致,从而达到消除混杂因素影响的目的。因此倾向性评分加权法是一种基于个体化的标准化法。
在实际的应用中,根据选择的标准化人群的不同,倾向性评分加权法可以分为逆概率处理加权法(the inverse probability of treatment weighting,IPTW)和标准化死亡比加权法(the standardized mortality ratio weighting,SMRW)。
IPTW法是以所有观察对象作为标准人群进行调整,暴露/处理组各观察对象的权重为Wt=Pt/PS,对照组各观察对象的权重为Wc=(1-Pt)/(1-PS)。(其中Pt为整个人群中接受暴露/处理因素的比例,PS为每个研究对象的倾向性评分)
SMRW法是以处理组观察对象作为标准人群进行调整,暴露/处理组各观察对象的权重为Wt=1,对照组各观察对象的权重为Wc=[PS(1-Pt)]/[(1-PS)Pt]。
当每一个观察对象的权重计算出来之后,就可以使用加权回归的方法来估计暴露/处理因素的效应值。
总结一下,倾向性分析的方法,是通过计算出每个研究对象的倾向性评分,从而可以用倾向性评分一个指标来集中体现多个混杂因素的综合影响,然后再使用分层、匹配、校正或加权等多种方法进行分析,以达到控制混杂因素的目的。
但是倾向性分析法依然无法解决由于混杂因素测量不准确,或者未知因素所引起的残余混杂作用。若想要在观察性研究中,使其结果接近RCT研究的理想状态,有没有更好的办法呢?在下一期内容中,我们将继续为大家介绍观察性研究中控制混杂因素的另一种新生代方法——工具变量分析。
4.工具变量分析
可以采用分层分析、多因素调整和倾向性分析等方法来对混杂因素加以控制,这些方法的优点在于使用起来相对简单,对结果的解释易于理解,但缺点在于它们仅能控制已测量到的混杂因素所引起的偏倚,而无法消除未知的、被遗漏的、以及测量不准确的混杂因素所造成的残余混杂。
为了进一步消除这部分残余混杂,2006年Brookhart等人首次从计量经济学中将工具变量分析(Instrumental Variable Analysis, IVA)的概念引入到观察性研究中,经过10年的发展,工具变量分析法在观察性研究中得到了越来越多的应用,今天我们就来向大家介绍一下这种在控制混杂因素家族中相对陌生的新方法。
工具变量分析
工具变量是指与研究暴露/处理因素相关,和其他混杂因素无关,并且和结局变量无直接关系的一类变量,它仅仅是通过与暴露/处理因素的关系,以及暴露/处理因素与结局变量的关系,来间接影响结局变量。
工具变量分析是一种用来控制测量误差和未知混杂因素引起的偏倚的估计方法,其基本思想为通过选择有效的工具变量,采用二阶段回归分析来消除未知混杂因素与暴露/处理因素之间的关系,使得混杂因素在暴露/处理组与对照组之间的分布是均衡的,从而获取暴露/处理因素对结局变量无偏的效应估计值。
工具变量满足条件
根据工具变量的定义,一个理想的工具变量应该满足以下几个条件:
1. 工具变量应与暴露/处理因素具有一定的相关性,其相关性的强弱称为工具变量的强度,可以通过第一阶段回归中工具变量的F统计量来检验。如果F统计量>10,则可认为是强工具变量,如果F统计量太小,则为弱工具变量,此时往往会导致效应估计值的置信区间较宽,容易得到无统计学意义的结果,增加了假阴性错误的概率,估计值的可信程度就会降低,缺乏实际的临床应用价值。
2. 工具变量除了通过暴露/处理因素的作用途径外,与研究结局没有任何直接或间接的关系。
3. 工具变量与其他任何已知的或未知的混杂因素均无相关关系。
针对以上条件,在选择工具变量时我们可以参考以下3个问题来帮助判断工具变量的选择是否合理:
1. Is the proposed instrumental variable associated with the likelihood of being exposed to the intervention? (所选择的工具变量是否与暴露/处理因素相关?)
Did the investigator report on the empirical association? (此相关是否有依可据?)
Is the magnitude of the association sufficiently strong? (是否为强关联?)
2. Is it very unlikely that the instrumental variable influences the outcome? (所选择的工具变量是否对研究结局没有影响?)
3. Have investigators demonstrated prognostic balance across the levels of instrumental variable? (在所选择的工具变量的不同水平分组下,预后因素是否达到了均衡?)(不是很理解???)
工具变量类型
目前文献中所报道的工具变量种类繁多。Journal of Clinical Epidemiology期刊于2011年发表了一篇系统综述,总结了5类在观察性研究中常用的工具变量类型,以供大家进行参考。
1. 基于不同地区医疗水平的差异,例如某个地区的医疗水平能够达到进行CT检查或心脏介入治疗的条件,那么该地区的患者则更倾向于接受相关治疗,同时地区因素与患者自身健康特征相关的因素并不相关,因此可以把地区作为一个工具变量。
2. 基于医疗机构的临床实践方式,例如以医疗机构使用某种治疗术式或药物使用的比例等作为工具变量。
3. 基于医生层面,例如以医生的处方偏好等作为工具变量。
4. 基于时间特性的工具变量,例如在评估流行性感冒疫苗疗效的研究中,以患者的痛风病史时间作为工具变量。
5. 基于以上变量综合起来的多个工具变量。
工具变量分析步骤
根据数据类型的不同,工具变量分析的算法常见的有以下几种:
1. 暴露/处理因素为连续型变量,结局也为连续型变量
暴露/处理因素及结局均为连续变量,例如研究运动时间对BMI的影响。对于此类因素,目前常用的最经典的工具变量分析方法为二阶段最小二乘法(2-stage least squares,2SLS)。(最小二乘法回归,即线性回归)
*第一阶段回归:以暴露/处理因素为因变量,以工具变量和已知的混杂因素为自变量进行普通最小二乘法回归,求 得 对 暴露/处理因素的估计值。第一阶段回归利用工具变量将暴露/处理因素分解为与混杂因素相关和不相关的两个部分。
*第二阶段回归:以结局变量为因变量,利用第一阶段回归中得到的暴露/处理因素的估计值替换暴露/处理因素的原始 值,并同时将已知的混杂因素作为自变量,再次进行普通最小二乘法回归,从而求得暴露/处理因素对于结局的效应估计值。
2. 暴露/处理因素为连续型变量,结局为分类变量
对于此种类型的研究数据,例如研究膳食纤维摄入量对肿瘤发病的影响,
*第一阶段回归与上述2SLS方法的第一步相同;
*第二阶段回归则利用logistic回归,来获得暴露/处理因素的效应估计值。
3. 暴露/处理因素为分类变量,结局也为分类变量
对于此种类型的研究数据,例如研究饮酒与食管癌发病的关联性,有研究人员采用了两阶段预测替代法(2-stage predictor substitution,2SPS)。
*第一阶段利用工具变量和协变量,与暴露/处理因素做logistic回归,得到暴露/处理因素的概率预测值,第二阶段利用概率预测值与结局变量再次进行logistic回归,以求得暴露/处理因素的效应估计值。
*若结局指标是生存数据时,在第二阶段可以采用风险比例模型,即Cox回归模型来进行估计。